1.3.6. Подбор подходящего теоретического распределения Критерии согласия

Для подбора подходящего теоретического распределения пре­жде всего следует построить экспериментальную кривую плот­ности распределения, после чего визуально выбрать похожую кривую из известных типов теоретических распределений. При построении экспериментальной кривой данные ран­жируют в порядке возрастания, разбивают на группы, строят гистограмму, а по ней - экспериментальную кривую. Разумеет­ся, что при наличии оснований отдать предпочтение тому или иному теоретическому закону распределения необходимость в построении экспериментальной кривой отпадает.

Выбрав тип предполагаемого теоретического распределения, выдвигают нулевую гипотезу о взаимном соответствии теорети­ческого и экспериментального распределений, проверяют ее на заданном уровне значимости, используя критерии согласия.

При больших выборках (n >100) предпочтение следует отда­вать критерию согласия Пирсона. Иногда этот критерий исполь­зуют при существенно меньших выборках. Критерий Колмого­рова— Смирнова дает хорошие результаты при n>30 и удов­летворительные при 100 > n >10. При n<10 лучшие результаты дает критерий Крамера - фон Мизеса. Эти рекомендации весьма приблизительны, так как каждый из критериев имеет свои сильные и слабые стороны, и от­носительно выбора между ними можно дать лишь самые общие указания.

Критерий Пирсона (хи-квадрат) применим только к сгруп­пированным данным. Рекомендуется, чтобы численность каждой группы (интервала) была не меньше 5. Если это не так, то смежные малочисленные группы следует объединять с сосед­ними.

Разбив исходные данные на т интервалов (групп), для каж­дого интервала вычисляют:

экспериментальные частоты р_i^* = n_i /n, где n_i - количество дан­ных, попавших в i-й интервал, п - общее количество данных (объем выборки);

теоретические частоты , найденные по таб­лицам или формулам для выбранного типа теоретического рас­пределения; экспериментальную величину

(1.54)

По таблицам квантилей распределения χ² при заданном уровне значимости β (обычно 5%) и известном числе степеней свободы f находят теоретическое значение χ². Число степеней свободы f равно количеству интервалов минус число независимых условий (связей), наложенных на эксперименталь­ные частоты р_i*. Примерами таких условий могут быть: равенст­во 1 суммы всех частот (такое условие накладывается всегда), совпадение статистического среднего с гипотетическим, совпаде­ние дисперсий и т. п. Следовательно f=т–1-r, где т - число интервалов, 1 - отмеченное выше условие, r -число парамет­ров, определяемых из опытных данных. Так, если предполага­емое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклоне­ние), поэтому f=т-1-r=т-1-2=т-3; при распределении по закону Пуассона, содержащему лишь один параметр λ, будем иметь r=1, поэтому f=т-1-2 =т—2. Если дополнительные условия (кроме первого) не наложены, то f = m -1.

При выполнении условия

(1.55)

считается, что при заданном уровне значимости (β=5%) функция распределения согласуется с экспериментальными данными.

Более жесткие требования по уровню значимости следует выдвигать с осторожностью. Увеличение доверительной вероят­ности уменьшает вероятность того, что незначимое различие будет принято за значимое и правильная функция будет отверг­нута. Однако это увеличивает вероятность того, что значимое различие будет принято за незначимое.

Во избежание возможных ошибок первого и второго рода, в особенности, если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличив число наблюдений, воспользоваться другим критерием согласия, вычислить асим­метрию и эксцесс и сопоставить их с известными для данного распределения.

Критерий Колмогорова - Смирнова определяется разностью максимальных абсолютных значений статистической функции распределения F* (х) и соответствующей теоретической функции распределения F(x), т. е.

(1.56)

Смирновым Н. В., а затем Колмо­горовым А. Н. было доказано, что ка­кой бы вид ни имела функция F(х), при неограниченном возрастании чи­сла независимых наблюдений п веро­ятность неравенства

(1.57)

стремится к пределу

(1.58)

Для практического использования критерия составлена табли­ца квантилей, определенных из соотношения k (λ_а)=α, где функция распределения записана в несколько ином виде:

Схема применения критерия Колмогорова — Смирнова сле­дующая.

По результатам п наблюдений строится (рис.1.18) статисти­ческая функция распределения F* (х).

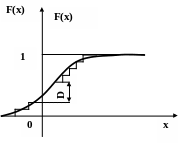
Рис. 1.18. К использова­нию критерия Колмого­рова

На том же графике наносится предполагаемая теоретическая функция распределения F(x).

Определяется максимальная величина модуля разности орди­нат D и вычисляется величина λ=D .

С помощью таблицы по заданному уровню значимости β (до­верительной вероятности α) находится значение λ_а. Если λ<λ_а, то теоретическое и экспериментальное распределения согласуются на заданном уровне значимости.