1.3. Подготовка данных и обработка результатов моделирования систем

Исходные данные для моделирования и его результаты часто представляют собой массивы случайных чисел. Это относится как к составляющим вектора внешних сил (постоянная нагрузка, временная нагрузка и др.), так и к выходным данным, например к результатам многократных повторений вычислительного эксперимента (прогонов модели). Такие массивы должны быть упорядо­чены с целью получения данных, удобных для моделирования или разработки практических рекомендаций по результатам мо­делирования. Обработку массивов случайных чисел производят по правилам математической статистики.

Остановимся на тех правилах, которые представляют непосредственный интерес для решения следующих задач:

• как подобрать подходящий теоретический закон распреде­ления случайных чисел с тем, чтобы использовать его для генерации случайных чисел при моделировании систем или для прогнозирования наибольших (наименьших) возмож­ных значений этих чисел;

• как правильно прогнозировать наибольшие или наимень­шие значения случайных чисел;

• как исключить ошибки получения экспериментальных дан­ных и как отсеивать ложные результаты;

• как найти минимальное, но необходимое число опытов, в том числе прогонов модели, для получения достоверных результатов;

• можно ли объединять две группы случайных величин в одну общую группу.

1.3.1. Случайные величины, законы их распределения

Случайной величиной х, или стохастической переменной назы­вают величину, наблюдаемое значение которой зависит от слу­чайных причин. Полный набор всех возможных значений, кото­рые принимает случайная величина х, называют генеральной сово­купностью. Набор случайно отобранных из генеральной совокуп­ности объектов называют выборочной совокупностью или просто выборкой. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 объектов (образцов, элементов, реализаций) отобрано 100, то объем генеральной совокупности N=1000, а объем выборки n=100. При больших объемах генеральной совокупности для облегчения теоретических построений объем генеральной совоку­пности часто принимают равным бесконечности.

Случайная величина характеризуется полностью, если указа­ны вероятности, с которыми она может принимать те или иные значения генеральной совокупности. Эти вероятности описывают с помощью интегральной функции распределения F(x) или с по­мощью дифференциальной функции плотности распределения f(x).

Плотностью распределения (или плотностью вероятности) f(x) называют предел отношения вероятности события, состоящего в том, что непрерывная случайная величина примет значение, лежащее в заданном малом интервале, к длине интервала, когда эта длина стремится к нулю. Про случайную величину X будем говорить, что она распределена с плотностью f(x) на таком-то участке оси абсцисс (рис.1.7,а). Заштрихованная на рисунке площадь равна вероятности того, что случайная величина X заключена в пределах участка [а, b], т. е.

(1.10)

Полная площадь, ограниченная кривой f(x), равна единице.

Функция распределения (рис.1.7,б) непрерывной случайной величины F(x) определяет вероятность того, что случайная вели­чина принимает значение не больше заданного, т. е.

(1.11)

Если известна функция распределения F(x), то вероятность, что величина х примет какое-нибудь значение в пределах ин­тервала [а, b], будет равна

(1.12)

Интегральная кривая этой функции монотонно возрастает от нуля (при х=-∞) до единицы (при х=∞). Обратная функция x=x(F_x) дает значения х, соответствующие заданной вероятности непревышения Р(х). Эти значения называют квантилями вероятности Р(х).

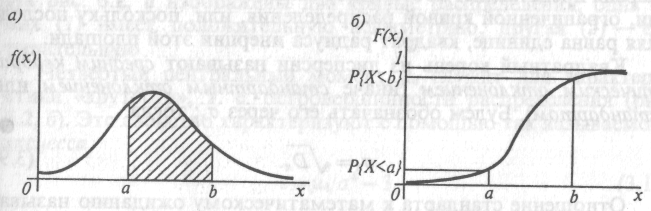
Рис. 1.7. Плотность (а) и функция (б) распределения

Функция распределения связана с плотностью распределения соотношениями:

(1.13) (1.14) (1.15)

Наиболее важной характеристикой случайной величины явля­ется ее среднее значение или математическое ожидание:

(1.16)

Математическое ожидание является центром распределения величины х. Геометрически т_х представляет собой абсциссу центра тяжести площади, ограниченной кривой плотности распределения и осью абсцисс.

Математическое ожидание квадрата отклонения величины х от центра ее распределения т_х, равное

(1.17)

называют дисперсией случайной величины х. Геометрически дис­персия представляет собой центральный момент инерции площа­ди, ограниченной кривой распределения, или, поскольку послед­няя равна единице, квадрат радиуса инерции этой площади.

Квадратный корень из дисперсии называют средним квадратическим отклонением (иначе стандартным отклонением или стандартом). Обозначим его через тогда

(1.18)

Отношение стандарта к математическому ожиданию называ­ют коэффициентом вариации

(1.19)

Иногда применяют следующие общеупотребительные обозна­чения математического ожидания и дисперсии:

(1.20)

Дисперсию удобно выражать через математическое ожидание:

(1.21)

т. е. дисперсия случайной величины равна математическому ожи­данию ее квадрата минус квадрат математического ожидания.

Числовые характеристики кривой распределения часто пред­ставляют в виде начальных моментов n-го порядка

(1.22)

и центральных моментов n-го порядка

(1.23)

Очевидно, что начальный момент первого порядка представ­ляет собой математическое ожидание; центральный момент пер­вого порядка равен нулю, а второго порядка — есть дисперсия случайной величины.

Третий центральный момент, разделенный на σ³, называют коэффициентом асимметрии

(1.24)

На рис.1.8,а изображены две кривые распределения; одна из них (1) имеет положительную асимметрию, другая (2) — от­рицательную.

Четвертый центральный момент μ₄ служит для характери­стики «крутости», т. е. островершинности распределения (рис.1.8,б). Это свойство характеризуют с помощью так называемого эксцесса

(1.25)

а саму величину μ₄/σ ⁴ называют куртозисом.

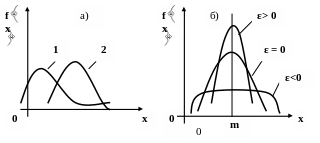
Рис.1.8. Асимметрия (а) и эксцесс (б) плотности распределения

Наряду с моментами, важной характеристикой случайной ве­личины является медиана, которая делит график плотности рас­пределения на две равные по площади части.

Если у случайной величины х существуют первый и второй моменты, то можно построить нормированную случайную вели­чину:

(1.26)

Для нормированной случайной величины

Понятие нормированных случайных величин важно потому, что для них построены многие таблицы распределений. При пользо­вании этими таблицами следует обратить внимание на запись функции. Например, функции нормаль­ного распределения для нормированной случайной величины (1.26) имеет вид:

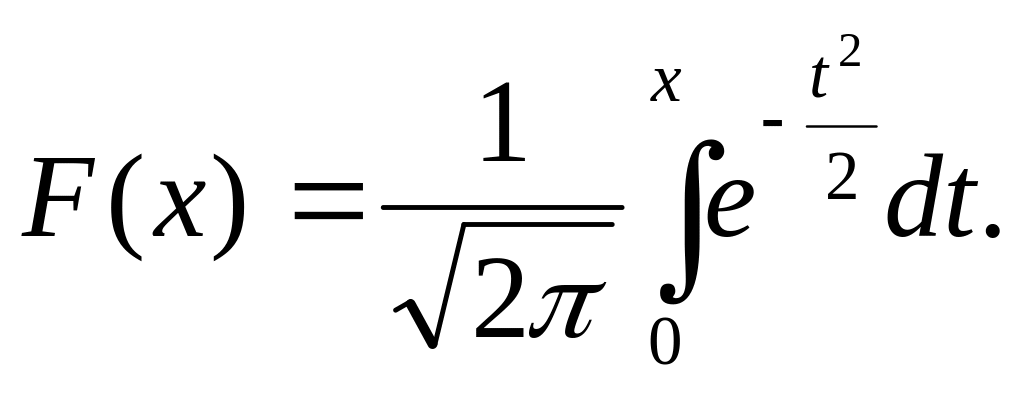(1.27)

В литературе приводят также таблицы функций нормального распределения, записанного в другом виде, поэтому следует про­являть осторожность и при пользовании другими таблицами обращать внимание на то, для какой функции они составлены.

Имеют место следующие соотношения между функциями рас­пределения, соответствующими нормированной величине z и не­нормированной величине х (величины без индекса 1 относятся к х, с индексом - к z):

(1.28)

(1.29)

(1.30)

(1.31)

Значения случайных величин, для которых численное значение интегральной функции распределения равно целому кратному от одной четверти, называют квартилями:

(1.32)

На графике плотности распределения квартили выделяют ту часть площади, которая равна 1/2, причем площади «хвостов» справа и слева равны между собой и равны 1/4.

Заметим, что второй квартиль — это медиана X_1/2=μ.