1.2.2. Математическое моделирование Виды математических моделей

Разнообразие систем и решаемых задач не позволяет дать четкую классификацию математических моделей по одному при­знаку. Их можно классифицировать по характеру отображаемых свойств объекта, принадлежности к иерархическому уровню, сте­пени детализации описания, способу представления свойств объекта и другим признакам. Мы условимся делить математические модели на два класса: структурные и функциональные, а последние, в свою очередь, будем подразделять на непрерывные и дискретные. Те и другие модели могут быть детерминированными и стохастическими. Кроме того, математическое моделирование может отображать как функциональное взаимодействие элементов системы, так и развитие процессов ее функционирования, и в этом смысле удобно рассматривать аналитическое, имитационное и комбини­рованное моделирование систем.

Структурные математические модели

Структурные математические модели предназначены для от­ображения структурных свойств объекта. Различают структур­ные модели топологические и геометрические.

Топологические математические модели отображают состав и взаимосвязи элементов объекта. Их чаще всего применяют для описания сложных объектов, состоящих из большого числа элементов, с целью привязки конструктивных элементов к опреде­ленным пространственным позициям (компоновка оборудова­ния, размещение деталей, трассировка соединений) или привязки собы­тий - к относительным моментам времени (разработка расписа­ний, составление графиков выполнения технологических опера­ций). Топологические модели могут иметь форму графов или соответствующих им матриц.

Геометрические математические модели отображают совокуп­ность данных, определяющих геометрическую форму объекта. Различают геометрические модели аналитические, алгебрологические, канонические, рецепторные, каркасные, кинематические и геометрические макромодели.

Аналитические геометрические модели представляют в виде уравнений, описывающих контуры или поверхности деталей. Эти уравнения могут задавать в декартовых, полярных и других системах координат. Форма представлений может быть явной y=f(x), неявной F(х, у)=0, или параметрической х=х(t), y=y(t).

Кинематические геометрические модели строят на основе ис­пользования параметрической формы записи поверхности. Та­кую поверхность можно получить путем перемещения в трехмер­ном пространстве некоторой кривой, называемой образующей. Эта кривая перемещается по другой кривой, которая называется направляющей линией. Например, если отрезок прямой переме­щать вдоль окружности, то будет образован цилиндр.

Геометрические макромодели являются математическим опи­санием типовых геометрических фрагментов (поперечных сече­ний металлопроката, подшипников, стандартных деталей, узлов и других типовых элементов чертежей). С помощью таких типовых элементов чертежей выполняют фрагменты чертежей и схемы конструкторско-технологической документации.

Функциональные математические модели

Математическую модель М объекта моделирования, т. е. системы S, можно представить в виде множества величин, описы­вающих процесс функционирования этого объекта и образующих в общем случае следующие подмножества [27] (рис.1.6): совокуп­ность входных воздействий на систему совокупность воздействий внешней среды совокупность внутренних (собственных) параметров системы совокупность выходных характеристик системы

При этом входные воздействия, воздействия внешней среды и внутренние параметры системы являются независимыми переменными, а выходные характеристики систе­мы - зависимыми переменными. Среди этих пере­менных могут быть управляемые и неуправляемые. Последние не зависят от желания расчетчика, работающего с моделью. Иногда управляемые величины называют параметрами.

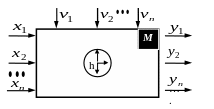
Рис. 1.6. Схема математической модели

Рассмотрим математическую модель для расчета пролетного строения моста. Постоянная, временная и другие нагрузки являются входными воздействиями. Выходными переменными являются показатели напряженно-деформированного состояния, управлять которыми расчетчик может путем изменения внутрен­них параметров системы. Последние могут быть представлены геометрическими характеристиками конструкций и физическими свойствами материала, из которого они изготовлены. Причем конструктивную схему пролетного строения и размеры его элементов обычно назначают предварительно и в этом смысле они являются неуп­равляемыми параметрами, а размеры поперечных сечений — ти­пичный представитель управляемых параметров. К воздействиям внешней среды здесь относятся возможные осадки опор и темпе­ратурные воздействия, которые вызывают появление дополни­тельных напряжений и тем самым влияют на выходные пе­ременные.

Математическое описание поведения объекта моделирования во времени t можно представить в следующем виде:

(1.8)

а для статических моделей - в форме равенства

(1.9)

Эти зависимости называются законами функционирования систе­мы: они могут быть заданы в виде функции, функционала, логи­ческих условий, или в алгоритмической либо табличной формах. Операторы F, f преобразуют независимые переменные в зависимые. Реализация этих преобразований выполняется с помощью алгоритма функционирования А. Один и тот же закон функционирования F системы S может быть обеспечен различными способами, т. е. с помощью множества различных алгоритмов функционирования А. Совокупность зависимостей выходных характеристик при законе функционирования типа (1.9) называется выходной траекторией. Если фиксировать отдель­ные моменты времени, то состояния системы S в эти моменты времени могут быть интерпретированы как координаты точки в фазовом пространстве. Причем каждой реализации процесса будет соответствовать некоторая фазовая траектория, а совокуп­ность всех возможных значений состояний называется простран­ством состояний объекта моделирования.