1.5.4. Подбор эмпирических формул по кривым
Подбор эмпирической формулы для установленной из опыта функциональной зависимости y=f(x) распадается на две части: сначала выбирают вид формулы, а затем - численные параметры, для которых приближение к данной функции является удовлетворительным. Вид формулы выбирают по каталогу кривых (см. ниже), параметры определяют по методу выравнивания. Метод выравнивания основан на предположении, что между у и х имеется линейная зависимость
(1.110)
Эта формула справедлива, когда экспериментальные точки прямой располагаются приблизительно на прямой линии. В тех случаях, когда этого нет и необходимо выбрать другую форму уравнения, надо преобразовать уравнение к виду:
(1.111)
вводя новые переменные
Ниже приведены наиболее часто встречающиеся кривые и соответствующие функциональные зависимости [3].
Формула
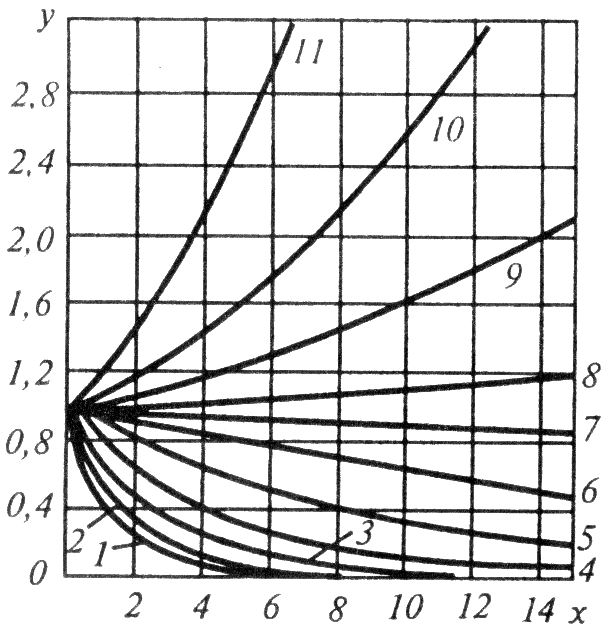
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
Формула
1)
2)
3)
4)
5)
6)
Формула
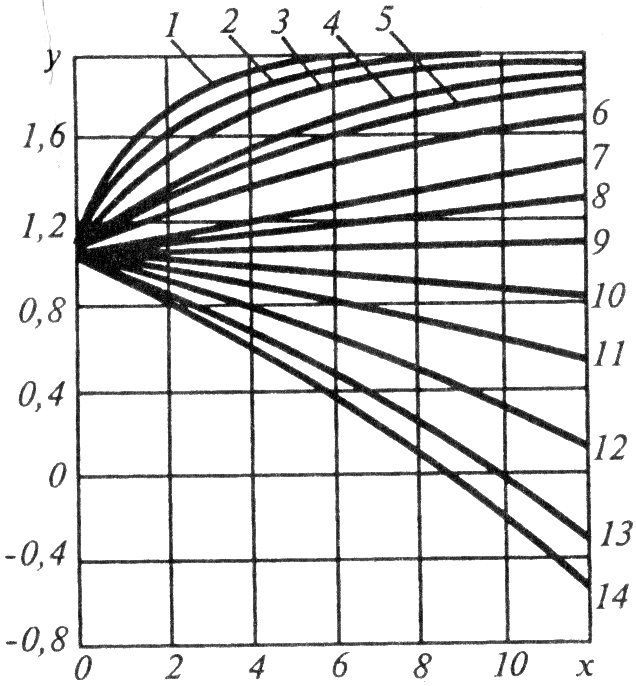
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
Формула
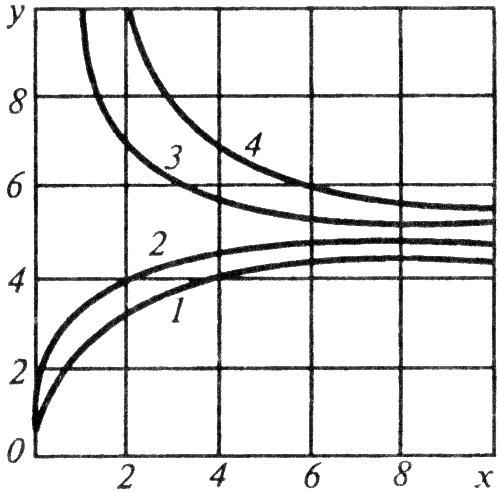
1)
2)
3)
4)
Формула y=axb+c
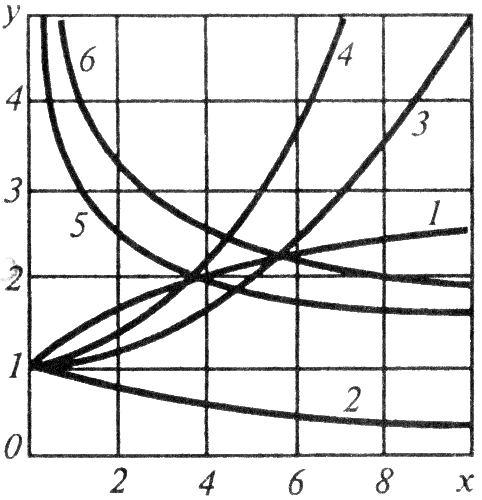
1)
2)
3)
4)
5)
6)
Формула
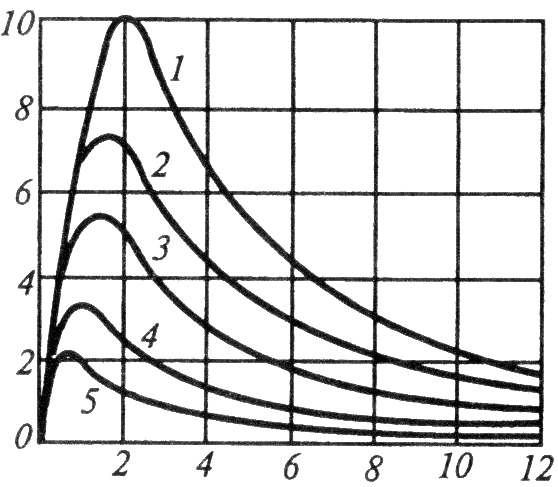
1)
2)
3)
4)
5)
Формула
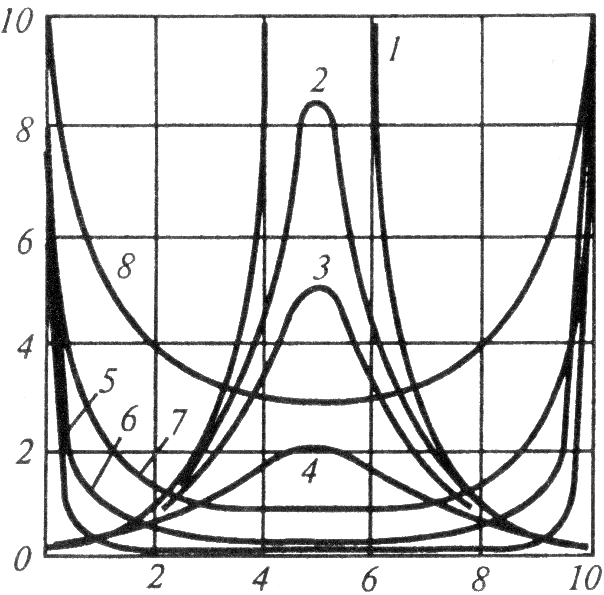
1)
2)
3)
4)
5)
6)
7)
8)
Вопросы к главе 1:
Какие существуют системы координат?
Что такое обобщенные силы и обобщенные переменные?
С помощью каких методов можно прогнозировать расчетные ситуации?
Как оценивается несущая способность конструкции?
Что такое резерв прочности?
Какие существуют виды моделирования конструкций транспортных сооружений ?
Какие существуют структурные математические модели?
Что такое случайная величина? Чем она характеризуется?
Какая взаимосвязь между «надежностью» и «обеспеченностью» при моделировании расчета строительных конструкций?
Что такое «нулевая», «альтернативная», «простая» и «сложная» гипотеза?
В каких случаях применим критерий Пирсона?
Как определяется область для управляемых и неуправляемых факторов при проведении эксперимента?
Опишите этапы планирования эксперимента.
Какой кривой заменяется диаграмма разброса при обработке и анализе результатов моделирования систем?