1.5.2. Метод наименьших квадратов

Рассмотрим особенности регрессионного анализа результатов моделирования на примере построения линейной регрессионной модели [16], [24].

Основы метода

На рис.1.24 показаны точки (x_i, у_i), полученные в эксперименте. Делаем предположение, что функция отклика может быть пред­ставлена в виде прямой линии

(1.85)

Требуется получить такие значения коэффициентов b₀ и b₁, при которых сумма квадратов ошибок будет минимальной. На ри­сунке ошибки e_t для каждой экспериментальной точки равны расстояниям по вертикали от этой точки до линии регрессии (1.85).

Обозначим (y_t)_i=b₀ + b₁ x_i (здесь (у_t)_i — величина, предсказыва­емая регрессионной моделью), тогда выражение для ошибок будет иметь вид

а функция ошибки

Для получения коэффициентов и , при которых функция F₀ будет минимальной, приравняем нулю част­ные производные и . Бу­дем иметь:

(1.86)

Таким образом, получена система двух линейных алгебра­ических уравнений:

(1.87)

Решая систему этих уравнений, получим

(1.88)

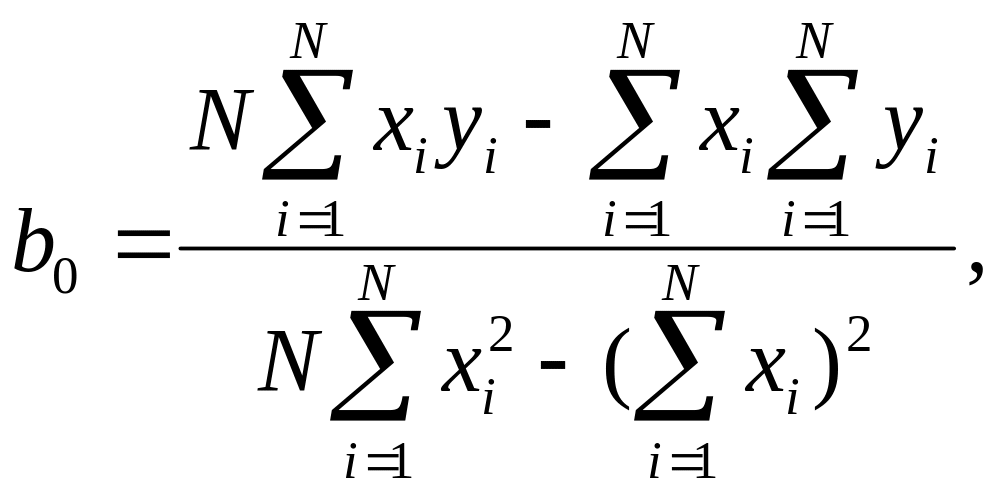
где N - число реализаций при моделировании.

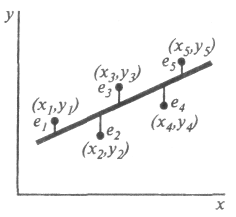
Рис.1.25. К построению рег­рессионной модели

Мы рассмотрели частный случай для уравнения (1.85). В более общем случае, когда эмпирическую функцию принимают в виде полинома

(1.89)

система уравнений типа (1.86), (1.87) будет иметь вид

(1.90)

Для оценки точности совпадения теоретических и эксперимен­тальных данных следует определить среднюю квадратичную ошибку на единицу веса

(1.91)

или среднее абсолютное отклонение

(1.92)

где r - число вычисляемых (табличных) значений; s - число параметров.

Последовательность обработки данных

Последовательность вычислений при построении уравнения регрессии на основе метода наименьших квадратов рассмотрим на конкретном примере [4].

Пример. Подобрать уравнение регрессии по экспериментальным дан­ным, приведенным ниже.

x	0	0,5	1,0	1,5	2,0
y	7,0	4,8	2,8	1,4	0

Решение. Вначале попытаемся в качестве типа эмпирической формулы при­нять линейную зависимость, удерживая в формуле (1.89) два первых члена:

Составим нормальные уравнения, для чего предварительно заполним табл.1.8. В таблице предусмотрим дополнительные столбцы 4, 5 и 8, которые нам могут потребоваться в дальнейшем.

Таблица 1.8

x°	x	x2	x3	x4	y	ху	x2y
1	2	3	4	5	6	7	8
1	0	0	0	0	7,0	0	0
1	0,5	0,25	0,125	0,0625	4,8	2,4	1,2
1	1,0	1	1	1	2,8	2,8	2,8
1	1,5	2,25	3,375	5,0625	1,4	2,1	3,15
1	2,0	4	8	16	0	0	0
5	5	7,5	12,5	22,125	16	7,3	7,15

Пользуясь данными столбцов 1, 2, 3, 6, 7, составим нормальные уравнения (1.90), которые применительно к нашему случаю при удержании только двух первых членов формулы (1.89) будут иметь вид:

Подставляя табличные данные, получим:

Решая эти уравнения, найдем: b_o = 6,68; b₁ = - 3,48, следовательно,

Оценим точность выполненных построений.

Подставив в полученную формулу значения х (табл.1.9), определим вычис­ленные значения у_t и отклонения.

Таблица 1.9

x	yt	y – yt	(y-yt)2
0 0,5 1,0 1,5 2,0	+ 6,68 +4,94 +3,20 + 1,46 -0,28	+0,32 -0,14 -0,40 -0,06 +0,28	0,1024 0,0196 0,1600 0,0036 0,0784

Суммируя данные последнего столбца, будем иметь:

Средняя квадратическая ошибка на единицу веса

Среднее абсолютное отклонение (1.97) равно

Полученные величины показывают, что формула подобрана неудовлетвори­тельно, так как исходные данные имеют точность до 0,1, а средняя квадратичес­кая ошибка на единицу веса значительно больше 0,1.

Повторим все операции, используя более точное выражение

Для записи нормальных уравнений (1.90) дополним вспомогательную табл.1.8 новыми данными, которые приведены в столбцах 4, 5, 8 и выделены курсивом. Составим нормальные уравнения:

После решения этой системы найдем b₀=7,00; b₁ = - 4,74; b₂ = 0,63 и запишем искомую зависимость:

Для определения средней квадратической ошибки составим табл.1.10.

Таблица 1.10

x	yt	y -yt	(y-yt)2
0 0,5 1,0 1,5 2,0	7,0 4,79 2,89 1,30 0,04	0 +0,01 -0,09 +0,10 -0,04	0 0,0001 0,0081 0,0100 0,0016

Суммируя последний столбец, получим ∑(у -у_t)²=0,0198.

Средняя квадратическая ошибка на единицу веса

Среднее абсолютное отклонение

Следовательно, формула у=7 - 4,74x+0,63 x² вполне удовлетворительно со­ответствует экспериментальным данным.