1.4.3. Общая схема планирования эксперимента Крутое восхождение

Рассмотренные выше приемы позволяют аппроксимировать поверхность отклика, если она в пределах исследуемой области линейна или близка к линейной. В общем случае поверхность отклика может иметь самую причудливую форму, напомина­ющую гористую местность с холмами и оврагами, с вершинами и впадинами. Задачей эксперимента часто является поиск экст­ремальных значений поверхности отклика: самой высокой вер­шины или самой глубокой впадины. Такую задачу решают мето­дом случайного или целенаправленного поиска. Случайный поиск или простой перебор точек факторного пространства требует очень больших затрат ресурсов, поэтому используют целенаправ­ленный перебор точек факторного пространства. Схема такого перебора («крутого восхождения») показана на рис. 1.21.

Вначале случайным образом выбирают достаточно малую область факторного пространства. Для этой области планируют дробный факторный эксперимент, проводят первую серию (обыч­но из четырех) опытов и строят линейную функцию отклика. Цель этих опытов - еще не поиск экстремального значения фун­кции, а предварительное отыскание направления дальнейшего поиска. Получив приближенное линейное уравнение, находят его градиенты (векторы производных по каждой переменной в каж­дой точке, или, другими словами, углы наклона поверхности в каждом направлении) и выбирают следующую область для приближенных исследований. В этой области вновь ставят серию опытов и определяют коэффициенты нового линейного прибли­жения. Повторяя такие операции, достигают, наконец, вершины поверхности отклика, т. е. такой области факторного пространст­ва, в которой по всем направлениям функция отклика практичес­ки не изменяется. В этой области проводят полный факторный эксперимент с определением не только линейных коэффициентов регрессии, но и всех учитываемых взаимодействий.

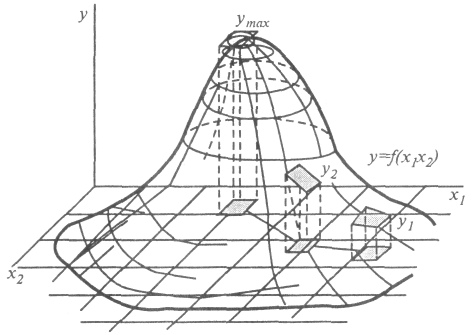
Рис. 1.21. Крутое восхождение

Направление градиента линейного приближения геометричес­ки представляет собой прямую, перпендикулярную изолиниям, т. е. это самый крутой склон (кратчайший путь), ведущий от данной точки к вершине, что и определило название метода. Рассмотренный подход был предложен в 1951 г. Боксом и Виль­соном.

Тот факт, что функция отклика в окрестности исследуемой точки почти не изменяется, еще не означает, что мы находимся вблизи точки максимума. Мы можем при этом находиться на медленно поднимающемся гребне или на гребне постоянной высоты. Возможно также, что достигнута седловидная точка, являющаяся максимальной точкой по одному направлению и ми­нимальной — по другому. Наконец, мы можем найти точку не глобального, а локального максимума. Надо заметить, что в ре­альных условиях, как правило, поверхность отклика имеет один максимум, и это упрощает дело.

Как уже отмечалось, в точке максимума следует проводить полный факторный эксперимент с учетом взаимодействий фак­торов. Более достоверные результаты дает квадратичное прибли­жение вида

Для оценки коэффициентов регрессии в этой модели необходимо измерить каждый фактор по меньшей мере на трех уровнях. Это означает необходимость проведения полного 3^m-факторного экс­перимента или его дробных реплик. К сожалению, в случае бо­лее чем трех переменных число опытов может стать слишком большим даже при использовании неполного факторного экс­перимента. Поэтому разработаны ротатабельные построе­ния, которые получаются посредством добавления дополнитель­ных точек к данным, полученным из 2^m-факторного эксперимен­та.