Лекция № 13 нелинейное программирование

Рассматриваемые вопросы

1. Постановка задачи нелинейного программирования.

2. Составление математической модели.

3. Графический метод решения задачи линейного программирования.

13.1. Постановка задачи нелинейного программирования

В общем виде задача нелинейного программирования (ЗНП) формулируется следующим образом:

(13.1)

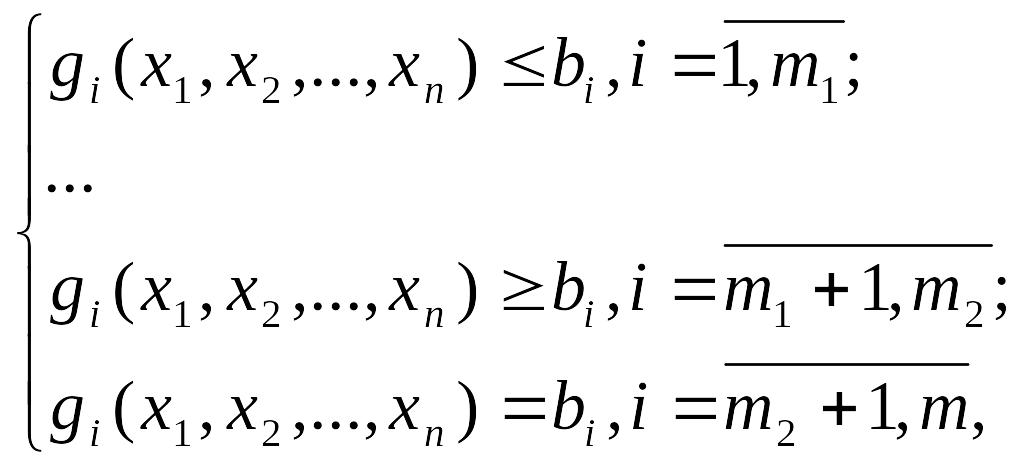(13.2)

где х_j – управляющие переменные или решения ЗНП, ;

b_i – фиксированные параметры, ;

f,g_i, – заданные функции от п переменных.

Если f и g_i линейны, то уравнения (13.1) и (13.2) переходят в задачу линейного программирования.

Решить задачу нелинейного программирования – это значит найти такие значения управляющих переменных x_j, которые удовлетворяют системе ограничений (13.2) и доставляют максимум или минимум функции .

Для задачи нелинейного программирования, в отличие от линейных задач, нет единого метода решения. В зависимости от вида целевой функции (13.1) и ограничений (13.2) разработано несколько специальных методов решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, ряд приближенных методов решения, графический метод.

Заметим, что нелинейное моделирование технических и экономических задач часто бывает искусственным. Большая часть проблем сводится к линейным моделям, поэтому в данном пособии нелинейные модели и методы расчета рассмотрены достаточно кратко.

13.2. Геометрическая интерпретация задачи нелинейного программирования. Графический метод решения

Рассмотрим задачу нелинейного программирования, содержащую две переменные.

(13.3)

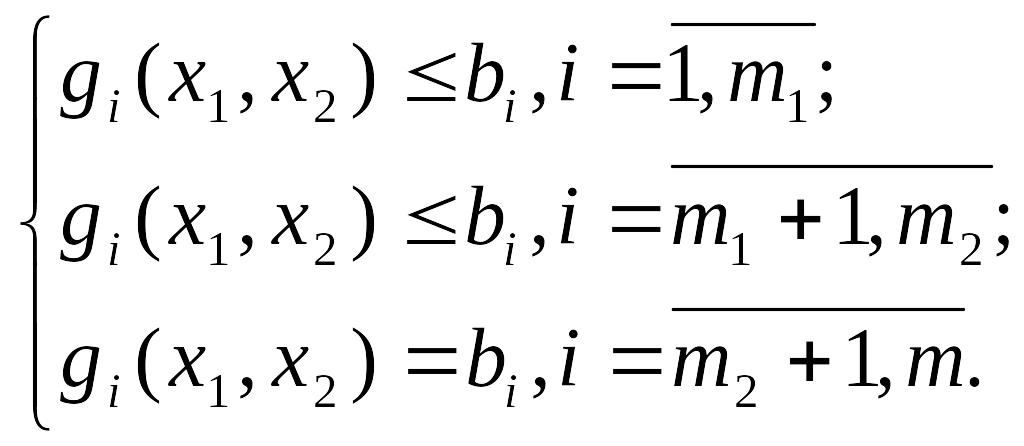(13.4)

Система ограничений (3.4) определяет в n-мерном пространстве некоторую область, которая является областью допустимых решений задачи.

Решить ЗНП графически – это значит найти точку в области допустимых решений (13.4), через которую проходит линия наивысшего (наинизшего) уровня.

Указанная точка может находиться как на границе, так и внутри области допустимых решений (13.4), в отличие от задач линейного програм­м­ирования.

Так же, как и для линейных задач, ЗНП удобно решать графически, когда функция и ограничения содержат две переменные.

13.3. Алгоритм решения знп графическим методом

Шаг 1. На плоскости x₁0x₂ строят область допустимых решений, определенную ограничениями (13.4). Если она пуста, т. е. ограничения несовместны, то задача (13.3)–(13.4) не имеет решения. В противном случае переходят к шагу 2.

Шаг 2. Строят линию уровня функции , где С – некоторая константа. Переход к шагу 3.

Шаг 3. Определяют направление возрастания (при максимизации), убывания (при минимизации) функции .

Шаг 4. Находят точку области допустимых решений, через которую проходит линия уровня с наибольшим (при максимизации), наименьшим (при минимизации) значением С или устанавливают неограниченность функции на области допустимых решений.

Шаг 5. Определяют значения x₁, x₂ для точки, найденной на шаге 4, и величину функции в этой точке.

Пример решения знп графическим методом

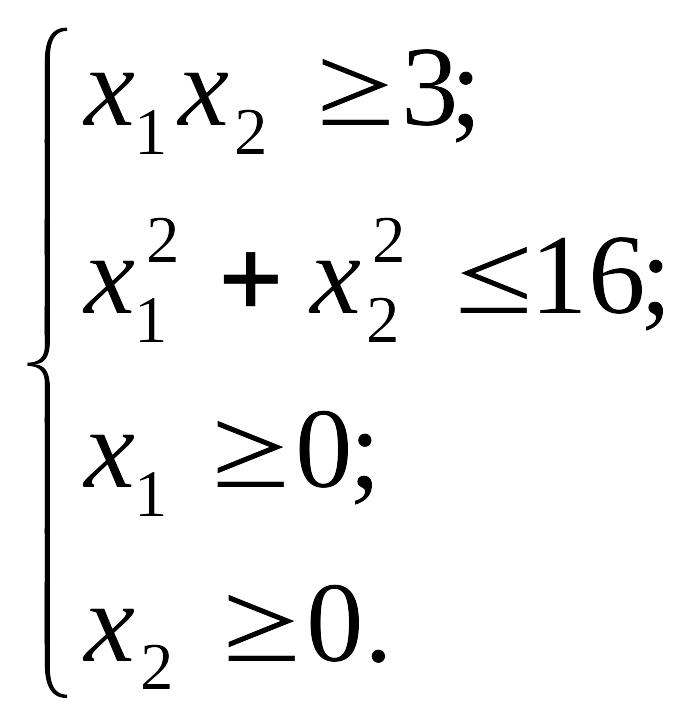
В соответствии с алгоритмом построим на плоскости x₁0x₂ область допустимых решений (рис. 13.1).

Ограничения , выделяют на плоскости x₁0x₂ первую четверть. Границей полуплоскости, соответствующей первому ограничению, является гипербола:

.

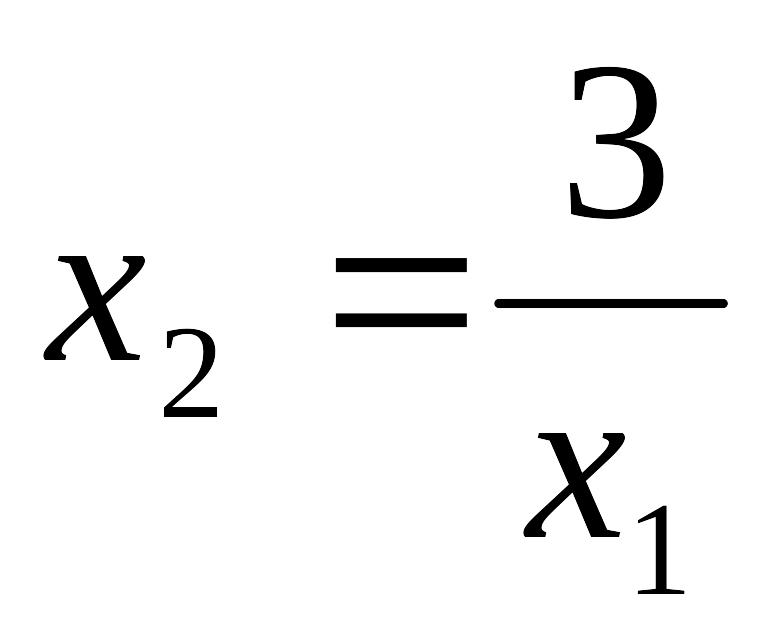Неравенство выполняется для точек, лежащих выше гиперболы. Границей полуплоскости, определяемой вторым ограничением, является окружность с центром в точке (0,0) и радиусом, равным 4. Искомая полуплоскость заштрихована вертикальной штриховкой. Область допустимых решений выделена горизонтальной штриховкой.

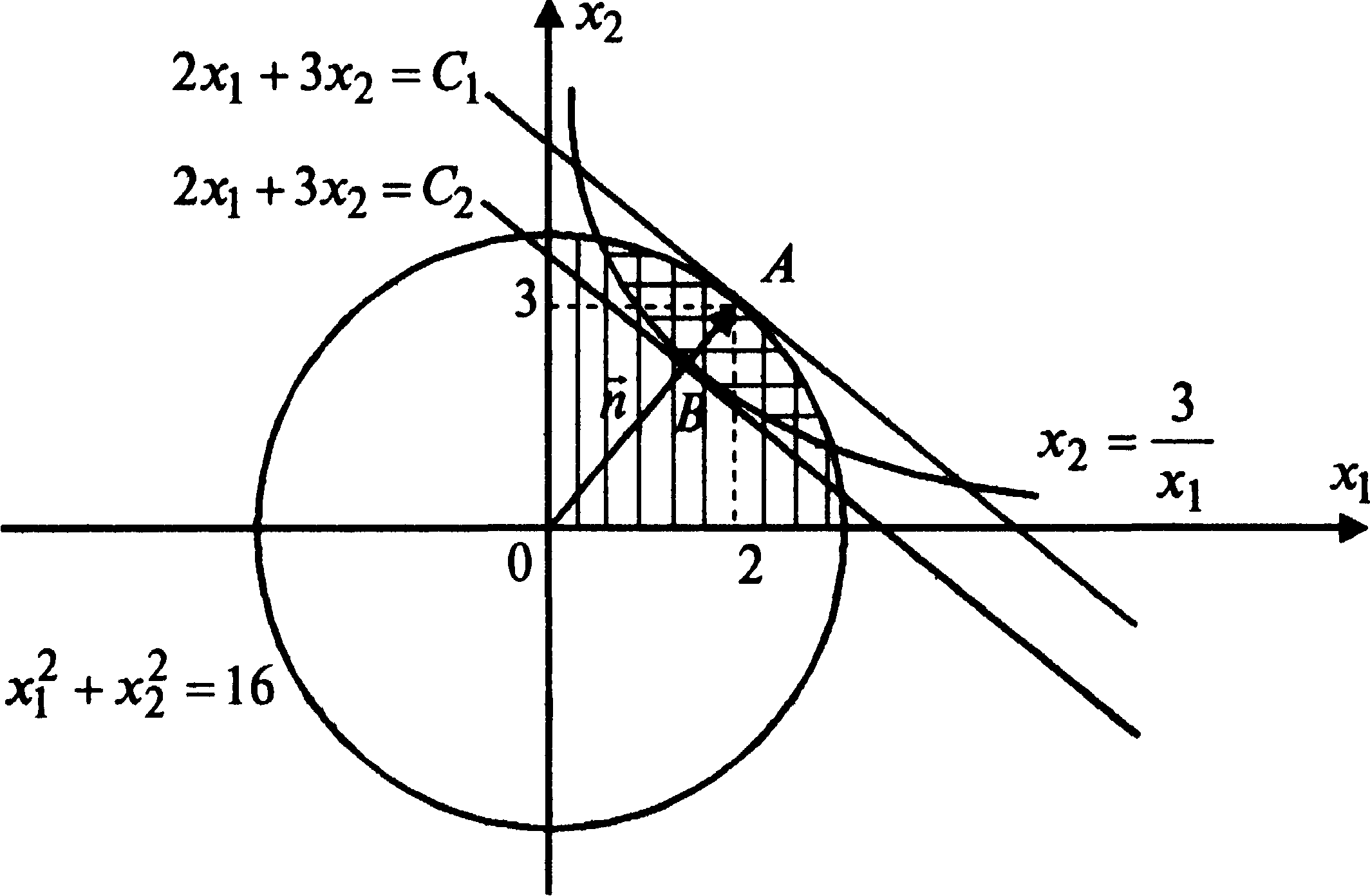
Рис. 13.1. Область допустимых решений

Функция возрастает в направлении вектора-нормали с координатами (2,3), и ее линии уровня расположены перпендикулярно вектору-нормали . Таким образом, максимум достигается в точке A, а минимум – в точке B.

Заметим, что в точке A совпадают тангенсы углов наклона касательной к окружности и прямой к оси 0x₁. Тангенсы углов наклона касательной и прямой к оси 0x₁ определяются значениями производных по x₁ соответствующих функций. Для прямой тангенс равен .

Продифференцируем выражение как неявную функцию от x₁. Получаем:

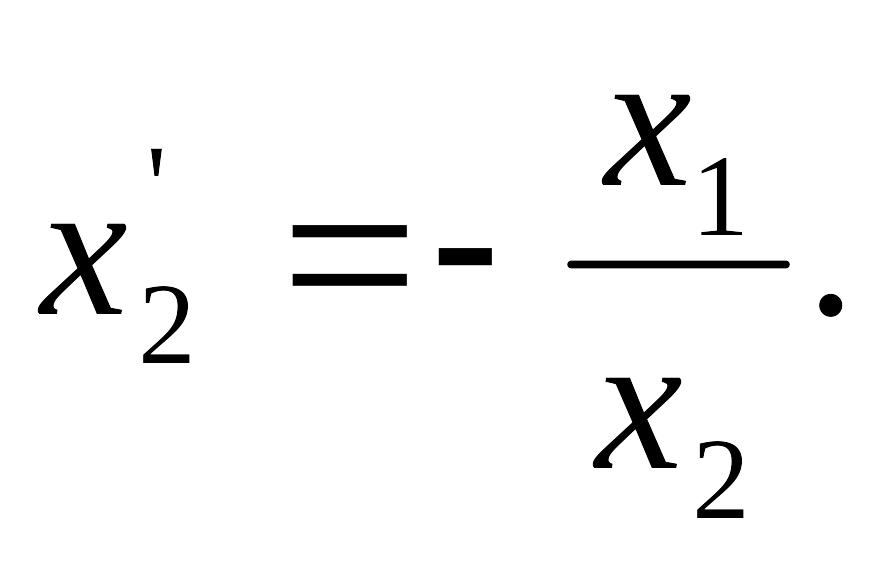
Приравниваем значения тангенсов, получаем:

;

.

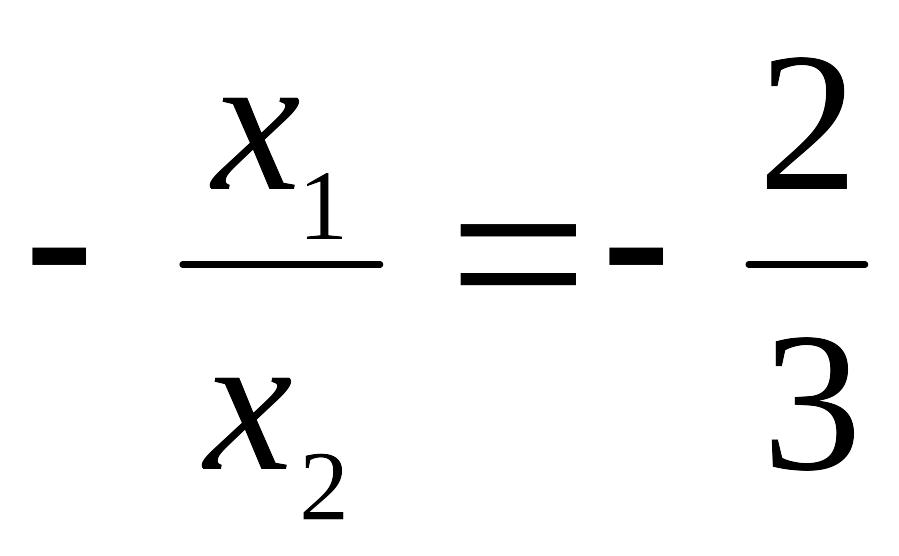К этому уравнению добавим уравнение окружности, которой принадлежит точка A. Получаем систему:

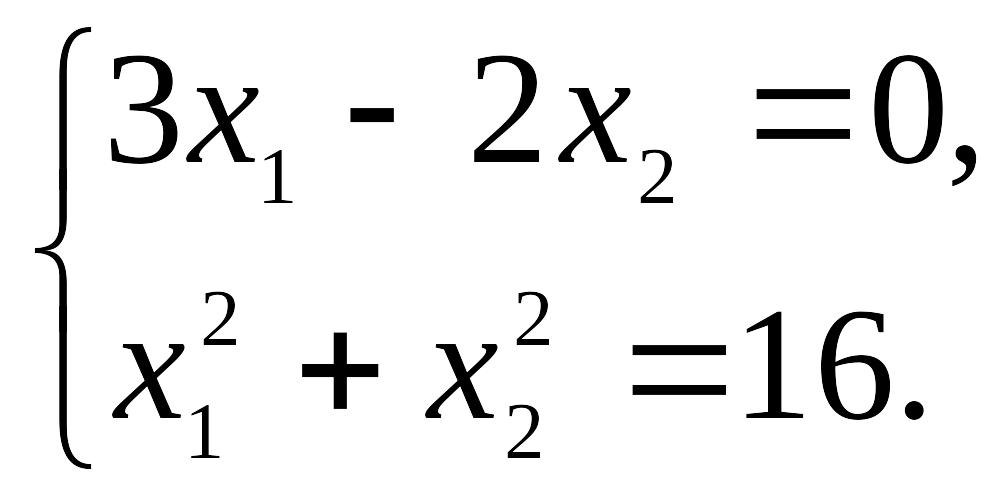
Решив ее, найдем оптимальное решение

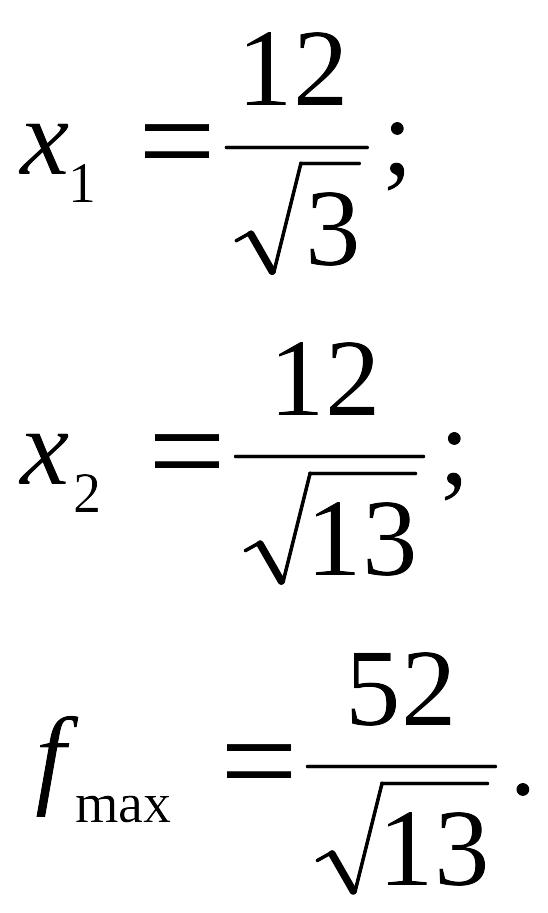
Аналогично определим координату точки B, в которой тангенс угла наклона к оси 0х₁ прямой совпадает с тангенсом угла наклона касательной к функции .

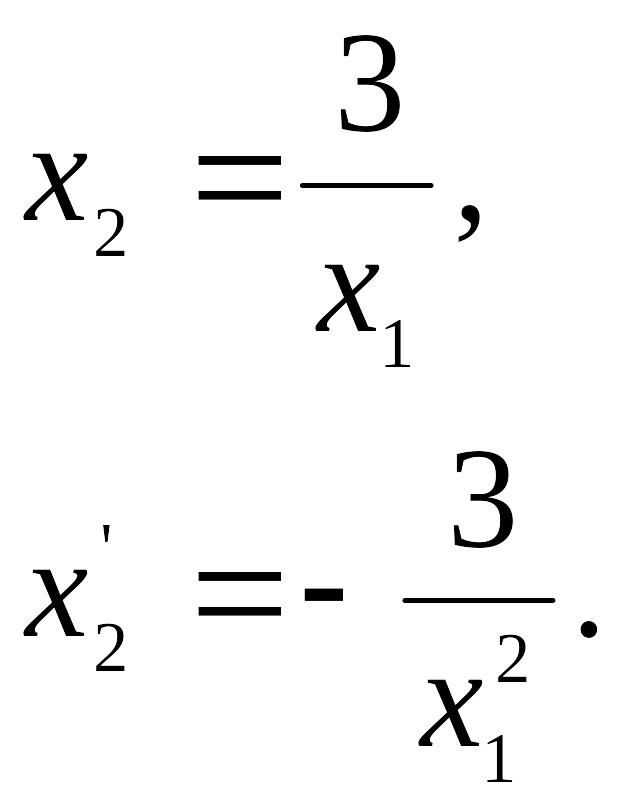
Получаем уравнение

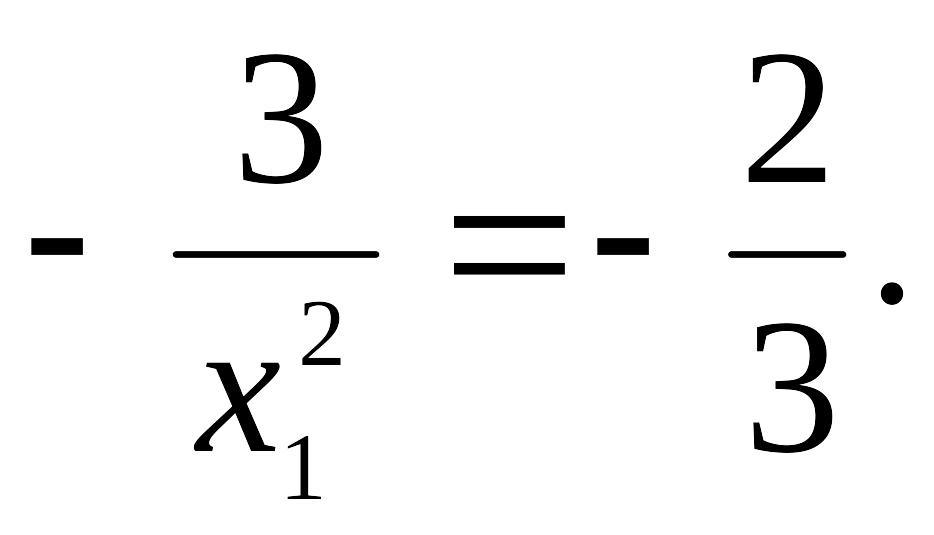
Вторым для нахождения координат точки является уравнение гиперболы, которой принадлежит точка B:

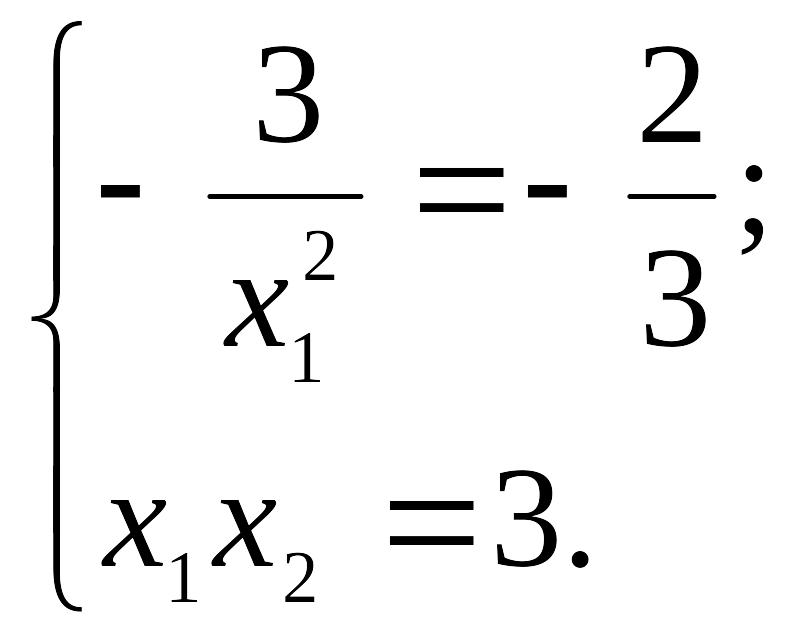
Из последней системы найдем оптимальное решение, соответствующее минимальному значению :