12.4. Решение задач линейного программирования на эвм

В общем виде система линейных алгебраических уравнений (СЛАУ) имеет следующий вид:

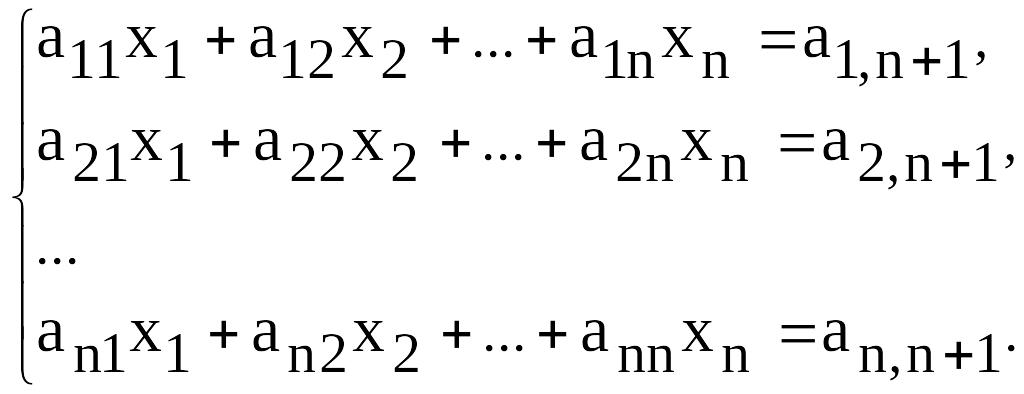(12.9)

где x_k – неизвестные величины; a_ij – заданные элементы расширенной матрицы системы уравнений.

Для решения СЛАУ применяют в основном два класса методов: прямые и итерационные. Прямые методы являются универсальными и применяются для решения систем сравнительно невысокого порядка (n не более 200). Итерационные методы выгодно использовать для СЛАУ высокого порядка со слабо заполненными матрицами.

12.5. Метод Гаусса с выбором главного элемента

Метод Гаусса относится к прямым методам. Алгоритм метода состоит из двух этапов. Первый этап называется прямым ходом метода и заключается в последовательном исключении неизвестных из уравнений, начиная с x₁.

Из первого уравнения системы (2.9) выражаем неизвестное x₁:

(12.10)

что возможно при , в противном случае надо осуществить перестановку уравнений системы. Согласно формуле (12.10) необходимо каждый элемент первой строки расширенной матрицы СЛАУ поделить на диагональный элемент:

. (12.11)

Затем выражение (2.11) подставляется во все остальные уравнения системы, тем самым исключается x₁ из всех уравнений кроме первого. Элементы расширенной матрицы преобразовываются по формуле:

(12.12)

В результате исключения первого неизвестного x₁ из всех уравнений системы (2.9), все элементы первого столбца преобразованной матрицы будут равны нулю, кроме .

Неизвестное x₂ выразим из второго уравнения системы (12.9) и исключим из остальных уравнений и т. д. В результате получим СЛАУ с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю.

Запишем выражения для неизвестных x_k и преобразования элементов расширенной матрицы системы, обобщающие формулы (12.10)–(12.12):

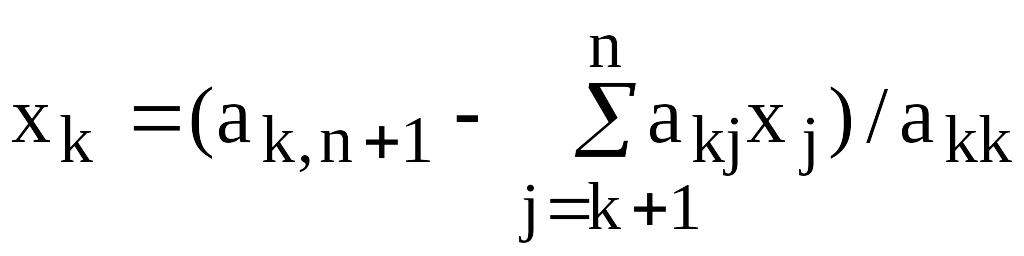; (12.13)

;

.

Второй этап решения СЛАУ называется обратным ходом метода Гаусса и состоит в последовательном определении неизвестных x_k по первой формуле (12.13), начиная с неизвестного x_n и заканчивая x₁.

Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент (вторая формула (12.13)) рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца.

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно 2/3n³. Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ и вычисления невязок r_k:

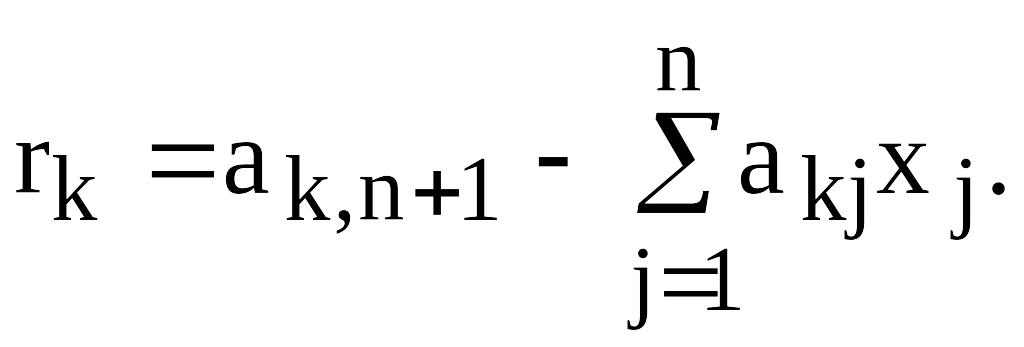При малой погрешности решений величины r_k будут близки к нулю.

12.6. Итерационные методы

Для решения СЛАУ итерационными методами преобразуем систему уравнений (12.9) к виду:

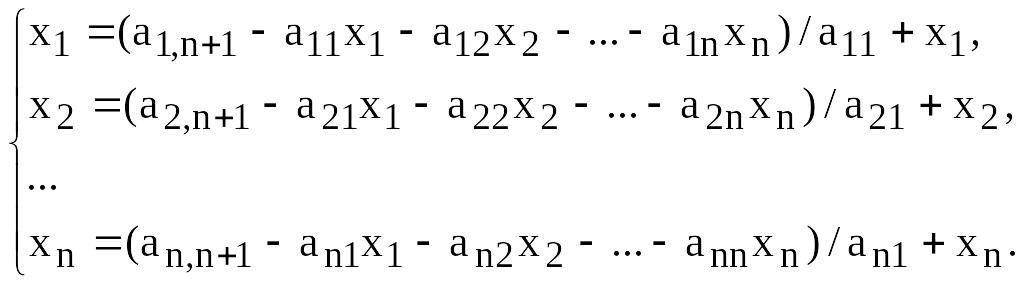(12.14)

Задается столбец начальных приближений , который подставляется в правую часть уравнений системы (12.14) и вычисляются новые приближения , которые опять подставим в систему (2.14), и так далее. Таким образом, организуется итерационный процесс, являющийся обобщением метода простых итераций на системы уравнений:

(12.15)

Процесс (12.15) можно видоизменить, если использовать приближения к решениям, найденные при выполнении текущей итерации. Такое изменение известно как метод Зейделя и, как правило, приводит к ускорению сходимости:

(12.16)

Для сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами. Условие сходимости можно обеспечить преобразованием исходной матрицы путем перестановки уравнений и неизвестных. Методы простых итераций Зейделя имеют разные области сходимости. Эти методы можно применять и к решению систем нелинейных уравнений.

Итерационный процесс заканчивается при выполнении условия:

где – заданная погрешность; k = 1, 2, ..., n.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте понятие линейного программирования.

2. В чем заключаются основные задачи линейного программирования?

3. В чем заключается стандартная задача линейного программирования?

4. Дайте понятие целевой функции.

5. Дайте понятие оптимизации.

6. графический метод решения задачи линейного программирования.

7. составление математической модели линейного программирования.