12.2. Графический метод решения задачи линейного программирования

При геометрическом рассмотрении задачи линейного программирования ее непустое множество допустимых решений образует выпуклый многогранник, целиком лежащий в области положительных значений переменных. В одной из крайних точек многоугольника решений целевая функция имеет оптимальное решение.

Таблица 12.1

Исходные данные задачи

Тип оборудования	Затраты времени, станко-ч		Фонд рабочего времени оборудования, ч
	А	Б
Токарное	4	16	320
Сварочное	8	3	240
Шлифовальное	6	7	210
Прибыль, тыс.руб	36	75

Порядок геометрического решения задачи линейного программирования рассмотрим на примере.

Для изготовления двух видов изделий А и В предприятие использует три вида оборудования: токарное, сварочное и шлифовальное. Затраты времени на обработку одного изделия для каждого типа оборудования, общий фонд рабочего времени оборудования и прибыль от реализации одного изделия приведены в табл. 2.1. Определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.

12.3. Составление математической модели

Предположим, что будет изготовлено единиц изделия А и единиц изделия В. Тогда для производства такого количества изделий А и В потребуется затратить станко-ч токарного оборудования, причем общий фонд рабочего времени станков данного типа не может превышать 320 ч, то есть

.

Аналогичные рассуждения относительно других типов оборудования приведут к следующим неравенствам:

;

.

Так как количество изготовленных изделий не может быть отрицательным, следовательно

;

.

Если будет изготовлено единиц изделия А и единиц изделия В, то прибыль от их реализации составит

.

Таким образом, приходим к следующей математической модели – определению максимального значения функции

при ограничениях

;

;

;

;

.

Решение

Воспользуемся геометрическим методом решения задачи. Данный метод решения включает в себя несколько этапов.

1. Производят построение прямых, уравнения которых получаются в результате замены в неравенствах ограничений знаков неравенств на знаки точных равенств:

;

;

;

;

.

Графическое построение проиллюстрировано на рис. 12.1.

2. Определяют полуплоскости, описываемые каждым из ограничений задачи.

Каждая построенная прямая делит плоскость на две полуплоскости. Координаты одной полуплоскости удовлетворяют исходному неравенству, а второй – не удовлетворяют. Чтобы определить искомую полуплоскость, нужно взять любую точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если удовлетворяют, то искомой является полуплоскость, которой принадлежит взятая точка, если не удовлетворяют, то другая полуплоскость. Искомая полуплоскость на графике обозначается стрелочками, направленными от прямой в сторону искомой полуплоскости (рис. 12.1).

3. Находят многоугольник решений.

Пересечения полученных полуплоскостей определяют многоугольник решений целевой функции (заштрихованная область на рис. 2.1).

4. Строят вектор С(36, 75), где 36 и 75 – коэффициенты целевой функции.

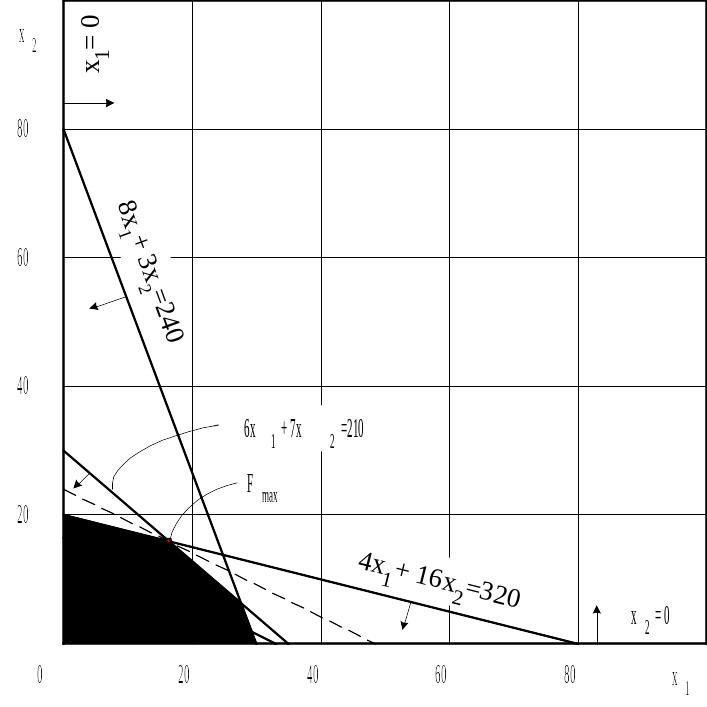
Рис. 12.1. Графическое решение задачи линейного программирования

5. Строят прямую , проходящую через многоугольник решений (прямая I на рис. 2.1).

6. Передвигая прямую параллельно самой себе в направлении вектора С, определяют точку (или точки), в которой целевая функция принимает максимальное значение (точка на рис. 12.1).

7. Определяют координаты точки максимума целевой функции и вычисляют значение функции в этой точке.

Так как точка является точкой пересечения двух прямых, то ее координаты удовлетворяют уравнениям следующей системы уравнений:

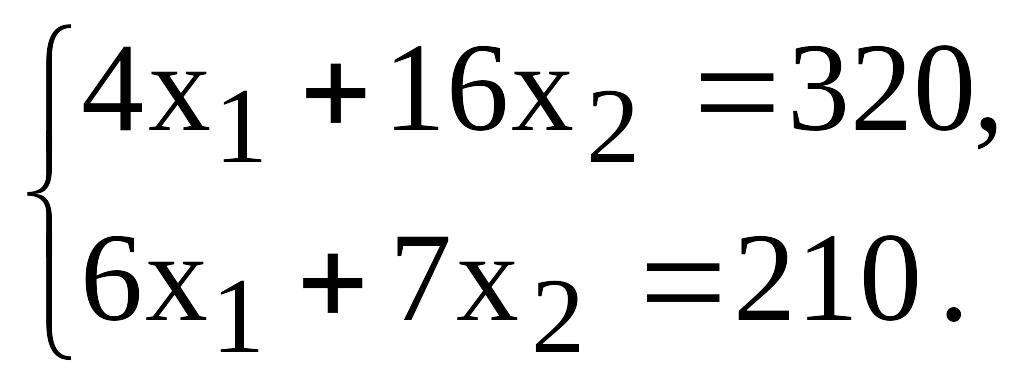
Решая полученную систему уравнений, получим следующие координаты и . В связи с тем, что значения переменных должны быть целыми, следовательно будем считать, что целевая функция имеет оптимальное значение в точке с координатами и .

Следовательно, если предприятие изготовит 16 изделий А и 15 изделий В, то оно получит максимальную прибыль, равную

тыс. руб.