Лекция № 12 Линейное программирование

Рассматриваемые вопросы

1. Постановка задачи линейного программирования.

2. Составление математической модели.

3. Графический метод решения задачи линейного программирования.

12.1. Общая и основная задачи линейного программирования

Во всех задачах линейного программирования требуется найти максимум или минимум некоторой линейной функции при условии, что ее переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств, или системе, содержащей как линейные неравенства, так и линейные уравнения.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

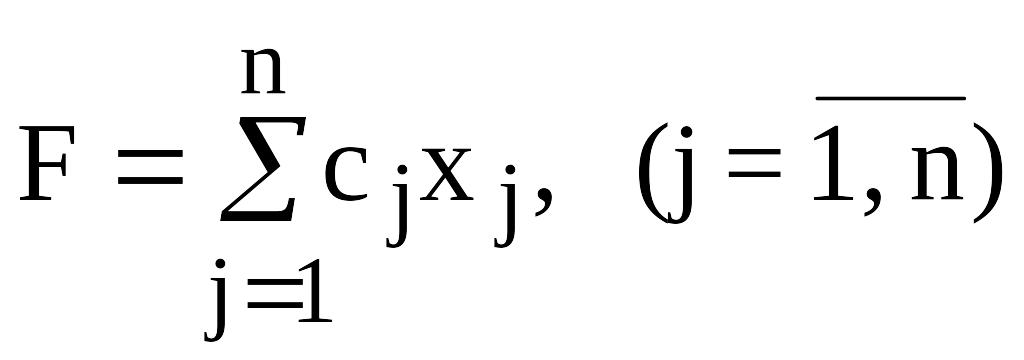; (12.1)

при условиях:

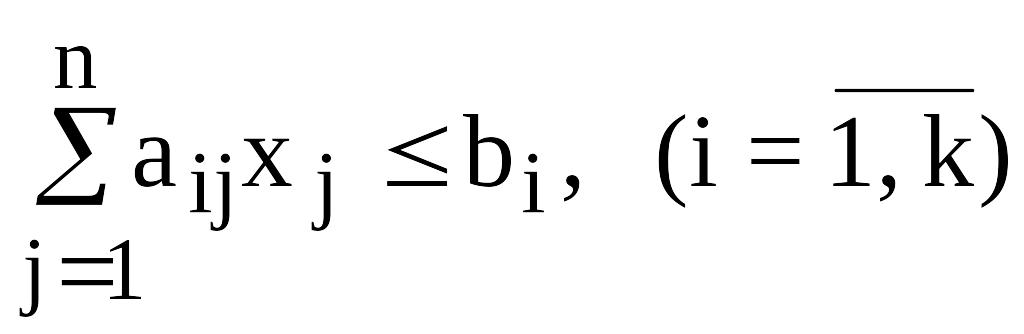; (12.2)

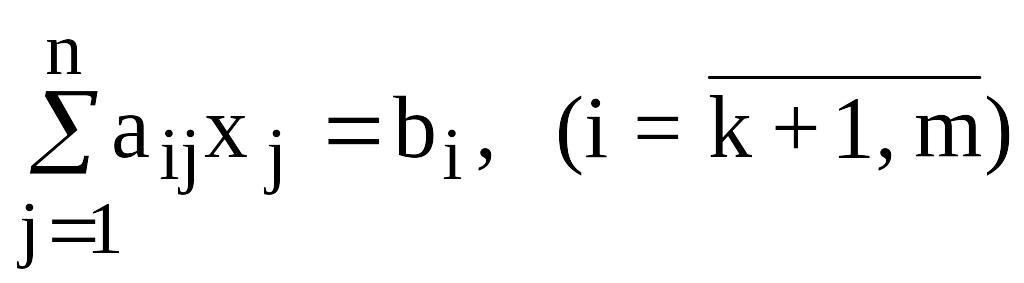; (12.3)

, (12.4)

где c_j – коэффициенты целевой функции (прибыль от единицы продукции, стоимость перевозок единицы груза и т. д.); a_ij – заданные коэффициенты ограничений или матрица технологических коэффициентов (расход сырья на единицу продукции, число рабочих занятых на одной операции и т. д.); b_i – заданная постоянная величина ограничения (запас сырья, наличие рабочей силы различной квалификации и т. д.); n – число переменных; m – число ограничений.

Выражение (12.1) называется целевой функцией задачи, а условия (12.2) - (12.4) – ограничениями данной задачи.

Стандартной задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (12.1) при выполнении условий (12.2) и (12.4), где k = m и .

Основной задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (12.1) при выполнении условия (12.3) и (12.4), где k = 0 и .

Совокупность чисел , удовлетворяющих ограничениям задачи (12.2)– (12.4), называется допустимым решением.

Допустимое решение , при котором целевая функция задачи (12.1) принимает свое максимальное (минимальное) значение, называется оптимальным.

Перечисленные три формы задачи линейного программирования эквивалентны между собой, так как с помощью несложных преобразований каждая из этих форм может быть записана в форме другой задачи. Для таких преобразований нужно в общем случае уметь:

● сводить задачу минимизации функции к максимизации и наоборот;

● переходить от ограничений в виде неравенств к ограничениям равенствам и наоборот;

● заменять переменные, которые не подчинены условию неотрицательности.

В случае, когда требуется найти максимум функции

, (12.5)

можно перейти к нахождению минимума функции

, (12.6)

поскольку функция F принимает максимальное значение в той же самой точке, в которой функция принимает минимальное значение.

Ограничение, являющееся неравенством, можно преобразовать в равенство добавлением к его левой части дополнительной неотрицательной переменной. Таким образом, ограничение

(12.7)

преобразуется в ограничение

. (12.8)

Если переменная не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными и , приняв x_k = u_k – v_k.