
Равномерное движение материальной точки по окружности
Движение по окружности является достаточно распространенным в окружающем нас мире: при вращении любого твердого тела вокруг фиксированной оси все точки этого тела движутся по окружностям. Так как все окружности подобны, то достаточно описать движение одной из них, чтобы описать вращение всего твердого тела. Кроме того, равномерное движение по окружности является простейшим криволинейным движением. Пусть материальная точка движется с постоянной по модулю скоростью v по окружности радиуса R. При таком движении направление вектора скорости v постоянно изменяется (рис. 71), следовательно, как и при любом криволинейном движении, движение по окружности есть движение с ускорением.
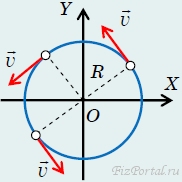
рис. 71
Рассмотрим изменение вектора скорости тела за малый промежуток времени Δt (рис. 72). Обозначим положение точки, движущейся по окружности радиуса R, в некоторый момент времени Аo.
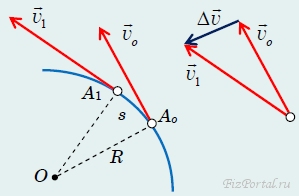
рис. 72
Вектор скорости vo в этот момент направлен по касательной к окружности, то есть перпендикулярно радиусу ОАo. За время Δt частица переместилась в точку A1, ее скорость v1 изменила направление и стала перпендикулярна радиусу ОА1 (но модуль ее остался неизменным: |vo| = |v1| = v). Для того чтобы вычислить изменение скорости, совместим начало векторов vo и v1. Тогда треугольник, образованный векторами скоростей, подобен треугольнику OAoA1. Из подобия этих треугольников следует
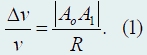
Если рассматривать изменение положения частицы и ее скорости за очень малый промежуток времени, то длина хорды |АoА1| будет очень близка к длине дуги АoА1
S = vΔt,
поэтому
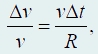
откуда получаем
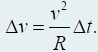
Таким образом, модуль ускорения точки равен:
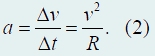
Чтобы полностью определить вектор ускорения, необходимо выяснить его направление. Заметим, что при малой величине Δt угол между векторами vo и v1 крайне мал, поэтому можно считать, что вектор изменения скорости направлен перпендикулярно1 как вектору vo, так и вектору v1. Следовательно, вектор ускорения в данном случае направлен к центру окружности. Вектор ускорения точки при ее равномерном движении по окружности направлен к центру окружности, а его модуль равен v2/R. Такое ускорение называется центростремительным. Как мы уже отмечали ранее, материальная точка, движущаяся по заданной линии, обладает одной степенью свободы, поэтому ее положение однозначно определяется одной координатой. В случае движения точки по окружности в качестве такой единственной координаты удобно выбрать угол поворота.
№8
Гелиоцентрическая система мира — представление о том, что Солнце является центральным небесным телом, вокруг которого обращается Земля и другие планеты. Противоположность геоцентрической системе мира. Возникло в античности, но получило широкое распространение с конца эпохи Возрождения.
В этой системе Земля предполагается обращающейся вокруг Солнца за один звёздный год и вокруг своей оси за одни звёздные сутки. Следствием второго движения является видимое вращение небесной сферы, первого — перемещение Солнца среди звёзд по эклиптике. Солнце считается неподвижным относительно звёзд.
№9
Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основная задача динамики
Прямая задача динамики: по заданным силам определить характер движения тела.
Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.
№10
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
![]() .
.
В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:
Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется.
№ 11
Первый закон Ньютона
Инерциальной называется та система отсчёта, относительно которой любая, изолированная от внешних воздействий,материальная точка либо покоится, либо сохраняет состояние равномерного прямолинейного движения.
Первый закон Ньютона гласит:
Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость постоянной, если на них не действуют другие тела и поля (или их действие взаимно скомпенсировано).
По сути, этот закон постулирует инерцию тел, то есть их свойство сопротивляться изменению их текущего состояния.
Второй закон Ньютона
Второй закон Ньютона— дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как мерило проявления инерции материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Второй закон Ньютона утверждает:
В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально приложенной к ней силе и обратно пропорционально её массе.
Третий закон Ньютона
Этот закон объясняет,
что происходит с двумя взаимодействующими
телами. Возьмём для примера замкнутую
систему, состоящую из двух тел. Первое
тело может действовать на второе с
некоторой силой  ,
а второе — на первое с силой
,
а второе — на первое с силой  .
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
.
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
Сам закон:
Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:
№12
Исаак
Ньютон выдвинул предположение, что
между любыми телами в природе существуют
силы взаимного притяжения. Эти силы
называют силами гравитации, или силами
всемирного тяготения. Сила всемирного
тяготения проявляется в Космосе,
Солнечной системе и на Земле. Ньютон
обобщил законы движения небесных тел
и выяснил,
что сила F равна:  массы взаимодействующих тел, R —
расстояние между ними, G — коэффициент
пропорциональности, который называется
гравитационной постоянной. Численное
значение гравитационной постоянной
опытным путем определил Кавендиш,
измеряя силу взаимодействия между
свинцовыми шарами. В результате закон
всемирного тяготения звучит так: между
любыми материальными точками существует
сила взаимного притяжения, прямо
пропорциональная произведению их масс
и обратно пропорциональная квадрату
расстояния между ними, действующая по
линии, соединяющей эти точки. Частным
видом силы всемирного тяготения является
сила притяжения тел к Земле (или к другой
планете). Эту силу называют силой тяжести.
Под действием этой силы все тела
приобретают ускорение свободного
падения. В соответствии со вторым законом
Ньютона g = Ft*m следовательно, Ft = mg. Сила
тяжести всегда направлена к центру
Земли. В зависимости от высоты h над
поверхностью Земли и географической
широты положения тела ускорение
свободного падения приобретает различные
значения. На поверхности Земли и в
средних широтах ускорение свободного
падения равно 9,831 м/с2.
массы взаимодействующих тел, R —
расстояние между ними, G — коэффициент
пропорциональности, который называется
гравитационной постоянной. Численное
значение гравитационной постоянной
опытным путем определил Кавендиш,
измеряя силу взаимодействия между
свинцовыми шарами. В результате закон
всемирного тяготения звучит так: между
любыми материальными точками существует
сила взаимного притяжения, прямо
пропорциональная произведению их масс
и обратно пропорциональная квадрату
расстояния между ними, действующая по
линии, соединяющей эти точки. Частным
видом силы всемирного тяготения является
сила притяжения тел к Земле (или к другой
планете). Эту силу называют силой тяжести.
Под действием этой силы все тела
приобретают ускорение свободного
падения. В соответствии со вторым законом
Ньютона g = Ft*m следовательно, Ft = mg. Сила
тяжести всегда направлена к центру
Земли. В зависимости от высоты h над
поверхностью Земли и географической
широты положения тела ускорение
свободного падения приобретает различные
значения. На поверхности Земли и в
средних широтах ускорение свободного
падения равно 9,831 м/с2.
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете (рис. 6). Вес тела обозначается Р. Единица веса — Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.
№13
Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Различают
среднюю мощность за промежуток времени
![]()
![]()
и мгновенную мощность в данный момент времени:
![]()
Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:
![]()
№14
"Потенциальная энергия - это энергия, запасенная объектом благодаря его положению или форме. Самолет приобретает потенциальную энергию, когда взлетает, преодолевая силы гравитации; когда он пикирует, эта потенциальная энергия высвобождается, превращаясь в кинетическую..." "Кинетическая энергия - это энергия движения. Движущийся самолет, подобно любому движущемуся телу, обладает кинетической энергией, которая падет до нуля, когда он останавливается..."
№15
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированнойфизической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.
В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.
Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике —теорема Пойнтинга.
№16
Теория строения жидкостей: сравнение со структурой газов и твердых тел Строение (структура) жидкостей. Структура жидкостей является в настоящее время предметом пристального изучения физико-химиков. Для исследований в этом направлении используются самые современные методы, включая спектральные (ИК, ЯМР, рассеивание света различных длин волн), рассеивание ренгеновских лучей, квантово-механических и статистических методов расчета и т.д. Теория жидкостей разработана гораздо хуже, чем газов, поскольку свойства жидкостей зависят от геометрии и полярности взаимно близко расположенных молекул. Кроме того, отсутствие определенной структуры жидкостей затрудняет их формализованное описание – в большинстве учебников жидкостям уделено гораздо меньше места, чем газам и твердым кристаллическим веществам. Каковы же особенности каждого из трех агрегатных состояний вещества: твердого тела, жидкости и газа. (таблица) 1) Твердое: тело сохраненяет объем и форму 2) Жидкость сохраняют объем, но легко меняют форму. 3) Газ не имеют ни формы ни объема. Эти состояния одного и того же вещества различаются не сортностью молекул (она одинакова), а тем как молекулы расположены и движутся. 1) В газах расстояние между молекулами много больше размеров самих молекул 2) Молекулы жидкости не расходятся на большие расстояния и жидкость в обычных условиях сохраняет свой объем. 3) Частицы твердых тел расположены в определенном порядке. Каждая из частиц движется около определенной точки в кристаллической решетке, подобно маятнику часов, т. е. колеблется. При понижении температуры жидкости затвердевают, а при повышении выше температуры кипения переходят в газообразное состояние. Уже этот факт указывает на то, что жидкости занимают промежуточное положение между газами и твердыми телами, отличаясь от того и другого. Однако жидкость имеет черты сходства с каждым из этих состояний. Существует такая температура, при которой граница между газом и жидкостью полностью исчезает. Это, так называемая, критическая точка. Для каждого газа известна температура, выше которой он не может быть жидким ни при каком давлении; при этой критической температуре исчезает граница (мениск) между жидкостью и ее насыщенным паром. Существование критической температуры ("температуры абсолютного кипения") установил Д.И.Менделеев в 1860 г. Второе свойство, объединяющее жидкости и газы – это изотропность. Т.е., на первый взгляд можно предположить, что жидкости ближе к газам, чем к кристаллам. Так же как и газы, жидкости изотропны, т.е. их свойства во всех направлениях одинаковы. Кристаллы, напротив, анизотропны: показатель преломления, сжимаемость, прочность и многие другие свойства кристаллов в разных направлениях оказываются различными. Твердые кристаллические вещества обладают упорядоченной структурой с повторяющимися элементами, что позволяет исследовать их методом дифракции рентгеновских лучей (метод рентгеноструктурного анализа, используется с 1912 г.).
№17
В окружающем нас мире происходят различного рода физические явления, которые напрямую связанны с изменением температуры тел. Еще с детства мы знаем, что холодная вода при нагревании сначала становится едва теплой и лишь спустя определенное время горячей.
Такими словами как «холодный», «горячий», «теплый», мы определяем различную степень «нагретости» тел, или, если говорить языком физики на различную температуру тел. Температура теплой воды немного выше температуры прохладной воды. Если сравнивать температуру летнего и зимнего воздуха, то разница в температуре очевидна.
Температура тел измеряется с помощью термометра и выражается в градусах Цельсия (°C).
Как известно, диффузия при более высокой температуре происходит быстрее. Из этого следует, что скорость перемещения молекул и температура глубоко взаимосвязаны между собой. Если увеличить температуру, то скорость движения молекул увеличится, если уменьшить – понизится.
Таким образом, делаем вывод: температура тела напрямую зависит от скорости перемещения молекул.
Горячая вода состоит из абсолютно таких же молекул, как и холодная. Разница между ними состоит лишь в скорости передвижения молекул.
Явления, которые имеют отношение к нагреву или охлаждению тел, изменению температуры, получили название тепловые. К ним можно отнести нагревание или охлаждение воздуха, плавку метала, таяние снега.
Молекулы, либо атомы, которые являются основой всех тел, находятся в бесконечном хаотичном движении. Количество подобных молекул и атомов в окружающих нас телах огромно. В объеме равном 1 см³ воды, содержится приблизительно 3,34 · 10²² молекул. Любая молекула имеет очень сложную траекторию движения. К примеру, частицы газа, передвигающиеся с большими скоростями в различных направлениях, могут сталкиваться как друг c другом, так и со стенками сосуда. Таким образом, они меняют свою скорость и опять продолжают движение.
Рисунок
№1 демонстрирует беспорядочное движение
частиц краски, растворенных в воде.
Таким образом, делаем еще один вывод: хаотичное движение частиц, которые составляют тела, называют тепловым движением.
Хаотичность является важнейшей чертой теплового движения. Одним из самых главных доказательств движения молекул является диффузия и Броуновское движение. (Броуновское движение – движение мельчайших твердых частиц в жидкости под воздействием ударов молекул. Как показывает наблюдение, Броуновское движение не может прекратиться).
В жидкостях молекулы могут колебаться, вращаться и двигаться относительно других молекул. Если брать твердые тела, то в них молекулы и атомы колеблются около некоторых средних положениях.
В
тепловом движении молекул и атомов
участвуют абсолютно все молекулы тела,
именно поэтому с изменением теплового
движения меняется и состояние самого
тела, его различные свойства. Таким
образом, если повысить температуру льда
то он начинает таять, принимая при этом
уже абсолютно другую форму – лед
становится жидкостью. Если же наоборот,
понижать температуру, к примеру, ртути,
то она изменит свои свойства и из
жидкости, превратится в твердое тело.

Температура тела напрямую зависит от средней кинетической энергии молекул. Делаем очевидный вывод: чем выше температура тела, тем больше средняя кинетическая энергия его молекул. И, наоборот, при понижении температуры тела, средняя кинетическая энергия его молекул уменьшается.
№19
Теорию, объясняющую строение и свойства тел на основе закономерностей движения и взаимодействия частиц, из которых состоят тела, называют молекулярно-кинетической. Основные положения молекулярно-кинетической теории (МКТ) формулируются следующим образом:
Любое вещество имеет дискретное (прерывистое) строение. Оно состоит из отдельных частиц (молекул, атомов, ионов), разделенных промежутками.
Частицы находятся в состоянии непрерывного хаотического движения, называемого тепловым.
Частицы взаимодействуют друг с другом. В процессе их взаимодействия возникают силы притяжения и отталкивания.
Справедливость МКТ подтверждается многочисленными наблюдениями и фактами. Наличие у веществ проницаемости, сжимаемости и растворимости свидетельствует о том, что они не сплошные, а состоят из отдельных, разделенных промежутками частиц. С помощью современных методов исследования (электронные и ионные микроскопы) получены изображения наиболее крупных молекул. Броуновское движение и диффузия свидетельствуют о том, что частицы находятся в непрерывном движении. Наличие прочности и упругости тел, явления смачивания, поверхностного натяжения в жидкостях и т.д. доказывают существование сил взаимодействия между молекулами. Масса и размеры молекул. Размер молекул является величиной условной. Его оценивают следующим образом. Между молекулами наряду с силами притяжения действуют и силы отталкивания, поэтому молекулы могут сближаться лишь до некоторого расстояния. Расстояние предельного сближения центров молекул называют эффективным диаметром молекулы. (При этом условно считают, что молекулы имеют сферическую форму.) С помощью многочисленных методов определения масс и размеров молекул установлено, что за исключением молекул органических веществ, содержащих очень большое число атомов, большинство молекул по порядку величины имеют диаметр 1• 10 - 10 м и массу 1• 10 - 26 кг. Относительная молекулярная масса. Относительной молекулярной (или атомной) массой Мr (или Аr) называют величину, равную отношению массы молекулы (или атома) mо этого вещества к 1/12 массы атома углерода mоС Относительная молекулярная (атомная) масса является величиной, не имеющей размерности. Количество вещества. Молярная масса. Масса молекулы. Количеством вещества ν называют величину, равную отношению числа молекул (или атомов) N в данном теле к числу атомов NA в 0,012 кг углерода, т.е. ν = N/ NA (NA - число Авогадро). Молярной массой М какого-либо вещества называют массу 1 моль этого вещества.
№20
Бро́уновское движе́ние — беспорядочное движение микроскопических, видимых, взвешенных в жидкости (или газе) частиц твёрдого вещества (пылинки, частички пыльцы растения и так далее), вызываемое тепловым движением частиц жидкости (или газа). Не следует смешивать понятия «броуновское движение» и «тепловое движение»: броуновское движение является следствием и свидетельством существования теплового движения.
В
математике, а точнее в теории
случайных процессов,
броуновское движение
(или винеровский
процесс) —
это гауссовский
процесс с
независимыми
приращениями,
у которого математическое
ожидание
равно нулю, а среднеквадратическое
отклонение
равно
![]() .
.
№21
Все частицы твёрдых и жидких веществ расположены близко, поэтому взаимодействуют всегда, и всегда обладают потенциальной энергией. Она зависит от сил взаимодействия с «соседками» и расстояний до них.
№22
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
![]()
№23
Моле́кула (новолат. molecula, уменьшительное от лат. moles — масса[1]) — электрически нейтральная частица, состоящая из двух или более связанных ковалентными связями атомов, наименьшая частица химического вещества. В физике к молекулам причисляют также одноатомные молекулы, то есть свободные (химически не связанные) атомы (например, инертных газов, ртути и т.п.). Причисление к молекулам одноатомных молекул, то есть свободных атомов, например одноатомных газов, приводит к совместимости понятий "молекула" и "атом" . Совмещение понятий "молекула" и "атом" идёт вразрез с атомно-молекулярным учением, по которому молекула образуется из атомов. Из одного атома молекула образоваться не может. Обычно подразумевается, что молекулы нейтральны (не несут электрических зарядов) и не несут неспаренных электронов (все валентности насыщены); заряженные молекулы называют ионами, молекулы с мультиплетностью, отличной от единицы (то есть с неспаренными электронами и ненасыщенными валентностями) — радикалами.Молекулы относительно высокой молекулярной массы, состоящие из повторяющихся низкомолекулярных фрагментов, называются макромолекулами.Особенности строения молекул определяют физические свойства вещества, состоящего из этих молекул.
№24
Для измерения термодинамической температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. Классическим примером термодинамического термометра может служить газовый термометр, в котором температуру определяют методом измерения давления газа в баллоне постоянного объёма. Известны также термометры абсолютные радиационные, шумовые, акустические.
Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).
Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.
Абсолютный ноль определён как 0 K, что равно −273 °C.
№25
Теория создана немецким физиком Р. Клаузисом в 1957 году для модели реального газа, которая называется идеальный газ. Основные признаки модели:
расстояния между молекулами велики по сравнению с их размерами;
взаимодействие между молекулами на расстоянии отсутствует;
при столкновениях молекул действуют большие силы отталкивания;
время столкновения много меньше времени свободного движения между столкновениями.
№26
Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.
Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.
№27
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
![]()
где
 —
давление,
—
давление,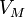 —
молярный объём,
—
молярный объём,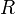 —
универсальная
газовая постоянная
—
универсальная
газовая постоянная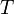 —
абсолютная
температура,К.
—
абсолютная
температура,К.
№28
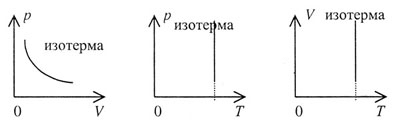
Закон Бо́йля — Марио́тта — один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Описывает поведение газа в изотермическом процессе. Закон является следствием уравнения Клапейрона.
Закон Бойля — Мариотта гласит:
При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.
В математической форме это утверждение записывается следующим образом
![]()
где
![]() —
давление газа;
—
давление газа;
![]() —
объём газа.
—
объём газа.
Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молярная масса газа, тем больше это отличие.
№29
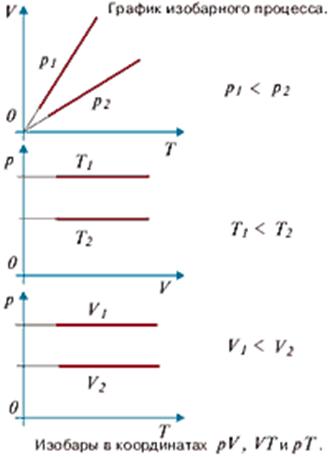
Закон Гей-Люссака — закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака, впервые опубликовавшего его в 1802 году.
Следует отметить, что в англоязычной литературе закон Гей-Люссака обычно называют законом Шарля и наоборот. Кроме того, законом Гей-Люссака называют также химический закон объёмных отношений.
Изобарический закон, открытый Гей-Люссаком в 1802 году утверждает, что при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Математически закон выражается следующим образом:
![]()
или
![]()
где
—
объём газа,
![]() —
температура.
—
температура.
Если известно состояние газа при неизменном давлении и двух разных температурах, закон может быть записан в следующей форме:
![]()
или
![]() .
.
№30
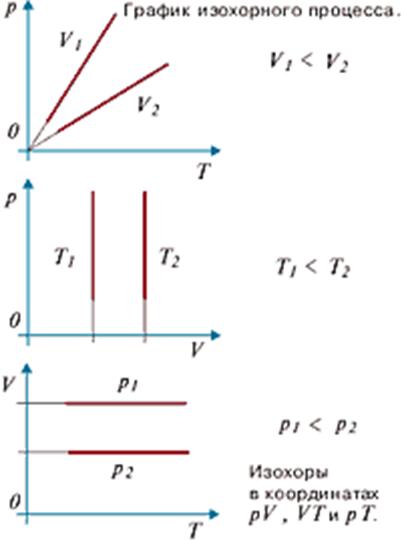
р = рoT, где р — давление газа при абсолютной температуре Т; рo — давление газа при температуре 0оС;
a — температурный коэффициент объемного расширения газа, равный 1/273 К-1.
В том случае, когда температура выражена по шкале Цельсия, то закон Шарля имеет вид:
pt=pо (1+t),
где t — температура по шкале Цельсия, pо — давление газа при t=0° C, pt — давление газа при температуре t, — коэффициент давления, для идеальных газов a=1/273.
Закон Шарля можно сформулировать и следующим образом: для данной массы газа отношение давления газа к его температуре постоянно, если объем газа не меняется:
P/Т=const, если V=const и m=const.
№31
Газы в технике, применяются главным образом в качестве топлива; сырья для химической промышленности: химических агентов при сварке, газовой химико-термической обработке
металлов, создании инертной или специальной атмосферы, в некоторых биохимических процессах и др.; теплоносителей; рабочего тела для выполнения механической работы (огнестрельное оружие, реактивные двигатели и снаряды, газовые турбины, парогазовые установки, пневмотранспорт и др.): физической среды для газового разряда (в газоразрядных трубках и др. приборах). В технике используется свыше 30 различных Г. |
№32
Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа не
зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости при
постоянном объёме, 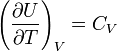 .
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
.
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
 .
.
Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае ![]() является
функцией и температуры, и объёма.
является
функцией и температуры, и объёма.
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
![]() ,
,
где ![]() —
количество вещества,
—
количество вещества, ![]() —
изменение температуры.
—
изменение температуры.
№33
