§3. Генеральная и выборочная дисперсии

Для характеристики рассеяния значений количественного признака генеральной совокупности вокруг своего среднего значения вводят свободные характеристики – генеральную и выборочную дисперсию (генеральное и выборочное среднее квадратическое отклонение).

О.1. Генеральной дисперсией называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Замечание 1. Если все значения признака генеральной совокупности объема различны, то

.

Замечание 2. Если значения признака имеют соответственно частоты , причем , то

.

О.2. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии, т.е.

.

О.3. Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений признака выборочной совокупности от их среднего значения .

Замечание 3. Если все значения признака выборочной совокупности объема различны, то

.

Замечание 4. Если значения признака имеют соответственно частоты , причем , то

.

Вычисление дисперсии, безразлично – выборочной или генеральной, можно упростить.

Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней, т.е.

.

Замечание 5. Если первоначальные варианты - большие числа, то для упрощения расчета удобнее вычесть из каждой варианты одно и то же число , т.е. перейти к условным вариантам , где - ложный нуль (число приблизительно равное выборочной средней, обычно это варианта расположенная в середине вариационного ряда; если таких вариант две, то лучше выбрать варианту с наибольшей частотой). Тогда

.

Замечание 6. Если первоначальные варианты являются десятичными дробями с десятичными знаками после запятой, то, чтобы избежать действий с дробями, можно умножить первоначальные варианты на постоянное число , т.е. перейти к условным вариантам . Тогда

.

О.4. Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии, т.е.

.

Замечание 7. При большом числе данных для вычисления выборочной средней и выборочной дисперсии используют метод произведений или метод сумм.

§4. Теоретические и эмпирические моменты

О.1. Начальным теоретическим моментом порядка признака называется математическое ожидание величины , т.е.

.

В частности

.

Используя начальные теоретические моменты 1-го и 2-го порядков можно записать формулу для вычисления дисперсии

.

О.2. Центральным теоретическим моментом порядка признака называется математическое ожидание величины , т.е.

.

В частности

.

Для вычисления выборочной средней и выборочной дисперсии удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям теоретических моментов. В отличие от теоретических эмпирические моменты вычисляются по данным наблюдений.

О.3. Обычным эмпирическим моментом порядка называют среднее значение -х степеней разностей , т.е.

,

где - наблюдаемая варианта,

- частота варианты,

- объем выборки,

- произвольное постоянное число (ложный нуль).

О.4. Начальным эмпирическим моментом порядка называют обычный момент порядка при , т.е.

.

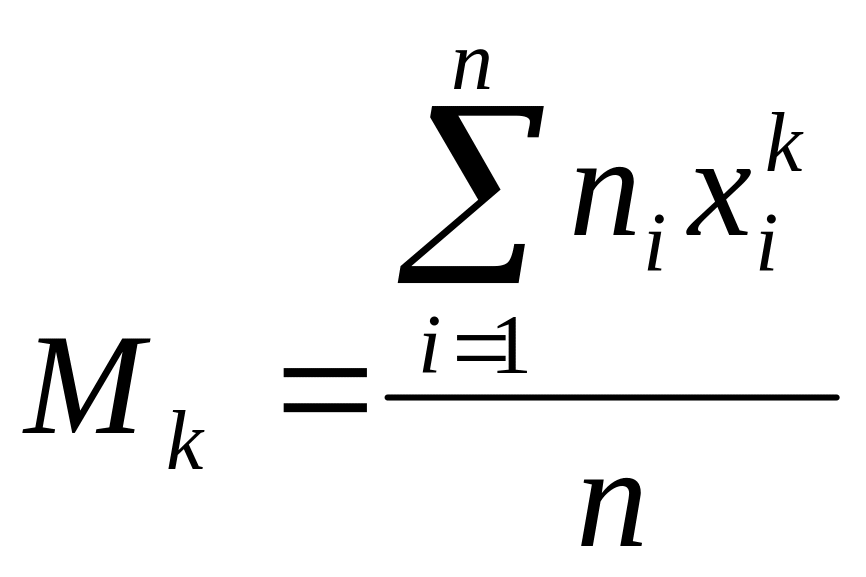В частности

.

О.5. Центральным эмпирическим моментом порядка называют обычный момент порядка при , т.е.

.

В частности

.

О.6. Условным эмпирическим моментом порядка называется начальный момент порядка , вычисленный для условных вариант , т.е.

,

где - шаг, разность между двумя соседними вариантами.

Выборочная средняя и выборочная дисперсия с использованием условных эмпирических моментов могут быть записаны в виде

.