§4. Линейная корреляция

О.1. Выборочным уравнением прямой линии регрессии на называется уравнение вида

,

где - условная средняя;

и - выборочные средние признаков и ;

- выборочные средние квадратические отклонения;

- выборочный коэффициент корреляции.

О.2. Выборочным уравнением прямой линии регрессии на

называется уравнение вида

,

где - условная средняя;

и - выборочные средние признаков и ;

- выборочные средние квадратические отклонения;

- выборочный коэффициент корреляции.

Пример 1. Найти выборочное уравнение прямой линии регрессии на по данным пяти наблюдений

	1	1,5	3	4,5	5
	1,25	1,4	1,5	1,75	2,25

Решение:

1) Составим расчетную таблицу

1	1,25	1	1,25	1,5625
1,5	1,4	2,25	2,1	1,96
3	1,5	9	4,5	2,25
4,5	1,75	20,25	7,875	3,0625
5	2,25	25	11,25	5,0625

2) Найдем выборочный коэффициент корреляции

Так как пары значений встречаются по одному разу, то формулу для коэффициента корреляции можно упростить

;

;

;

;

;

;

;

.

3) Найдем уравнение прямой линии регрессии

,

4) Изобразим на графике полученную линию и данные выборки

Замечание 1. При большом числе наблюдений одно и то же значение может встретиться раз, одно и то же значение - раз, одна и та же пара чисел может наблюдаться раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты . Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Устройство корреляционной таблицы

В первой строке таблицы указаны наблюдаемые значения признака , а в первом столбце – наблюдаемые значения признака . На пересечении строк и столбцов этой таблицы отмечаются частоты , наблюдаемых пар значений признаков. В последнем столбце записываются суммы частот строк , а в последней строке - суммы частот столбцов . В клетке в правом нижнем углу таблицы записывается сумма всех частот .

Пример 2. Выборка представлена в виде корреляционной таблицы

	15	20	25	30	35	40
100	2	1	-	7	-	-	10
120	4	-	2	-	-	3	9
140	-	5	-	10	5	2	22
160	-	-	3	1	2	3	9
	6	6	5	18	7	8	50

Замечание 2. Если данные наблюдений над признаками и заданы в виде корреляционной таблицы с равноотстоящими вариантами, то удобнее перейти к условным вариантам:

;

,

где и - ложные нули вариант и соответственно;

и - шаги, т.е. разности между двумя соседними вариантами

и соответственно.

Замечание 3. В случае если был осуществлен переход к условным вариантам, выборочный коэффициент корреляции примет вид

,

где величины могут быть найдены либо методом произведений (при большом числе данных), либо непосредственно по формулам выборочного среднего и выборочного среднего квадратического отклонения.

Замечание 4. Зная величины можно определить входящие в уравнения регрессии величины по формулам

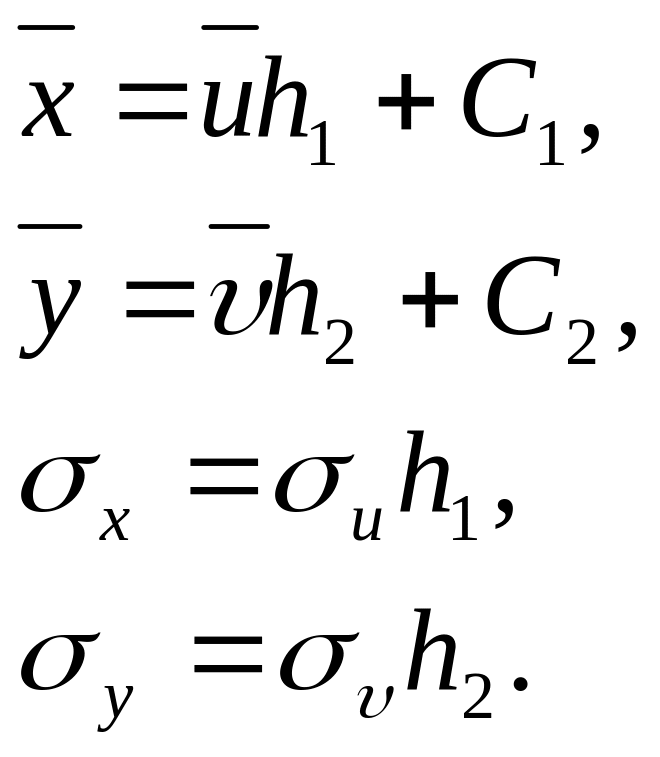
Пример 3. Найти выборочное уравнение прямой линии регрессии на по данным корреляционной таблицы примера 2.

Решение:

1) Составим корреляционную таблицу в условных вариантах, с учетом того, что , , ,

	-3	-2	-1	0	1	2
-1	2	1	-	7	-	-	10
0	4	-	2	-	-	3	9
1	-	5	-	10	5	2	22
2	-	-	3	1	2	3	9
	6	6	5	18	7	8

2) Составим расчетную таблицу для нахождения суммы

следующим образом:

1. В каждой клетке, в которой частота , запишем в правом верхнем углу произведение частоты на варианту .

2. Сложим все числа, записанные в правых верхних углах клеток одной строки и их сумму запишем в клетку этой же строки столбца .

3. Умножим варианту на и полученное произведение запишем в последнюю клетку той же строки, в клетку столбца .

4. Сложим все все числа столбца и получим сумму , которая равна искомой сумме.

5. Для контроля аналогичные вычисления проведем по столбцам.

	-3	-2	-1	0	1	2
-1	2	1	-	7	-	-	-8	8
0	4	-	2	-	-	3	-8	0
1	-	5	-	10	5	2	-1	-1
2	-	-	3	1	2	3	5	10
	-2	4	6	5	9	8	-
	6	-8	-6	0	9	16

Контроль:

3) Найдем

4) Найдем

5) Найдем

6) Вычислим

7) Выполним переход к исходным вариантам

8) Найдем уравнение регрессии на