
- •8.Математикалық қабілеттердің негізгі компоненттері. Оқушылардың математикалық қабілеттерін дамыту.
- •10.Математиканы есептер арқылы оқыту.
- •11.Оқушыларға теориялық білім беруге ,математикалық іскеерлікті қалыптастыруға бағытталған есептер.
- •13.Мұғалімнің сабаққа дайындық жүйесі
- •14 .Өз бетімен жұмыстың математиканы оқытуда алатын орны.Ты Өз бетімен жұмыс ұйымдастыру жолдары.
- •15.Математикадан факультативтік сабақтар және оларды жүргізу әдістемесі.
- •16. Математикадан сыныптан тыс жұмыстардың мақсаты, мазмұны және негізгі түрлері. Математикалық үйірме.
- •17.Математиканы тереңінен оқытатын мектептерде ,орта арнаулы кәсіби оқу орындарында және т.Б мектертерде математиканы оқыту ерекшеліктері.
- •19. Жиын уғымы. Жиынның элементтері
- •21.Есептеу және тепе-тең түрлендірудің тәсілдері және оларға қойылатын талаптар. Ауызша есептеу және тепе-тең түрлендірулер.Жазбаша есептеулер.
- •Функцияның берілу тәсілдері
- •23.Мектеп курсы математиксында теңдеулер мен теңсіздіктерді және олардың жүйесін оқыту әдістемесі.
- •30.Туындының қолданбалы жерлері
- •32.Көпжақтарды оқытудың мазмұны мен құылымы.
- •39. Чева теоремасы.
30.Туындының қолданбалы жерлері
Туынды ұғымы XVII ғасырда бір-бірінен тәуелсіз, екі бөлек тәжірибе арқылы И.Ньютон мен Г.Лейбництің есептеулерінде пайда болды. И.Ньютон есептеулерді механикаға байланысты (қозғалыстағы дененің жылдамдыы арқылы), ал Лейбниц геометрияға байланысты (шексіз аз шама) жүргізді. Ал, бұған дейін туынды ұғымы итальян математигі Тартальи (шамамен 1500-1557) еңбектерінде кездескен. Тартальи еңбектеріндегі туынды ұғымы снарядтың ең үлкен қашықытықа ұшуы кезіндегі қарудың бұрыштық иілуінде жанаманың пайда болуында байқалады. 1684 жылы Г.Лейбниц Лейпцигтік «Acta Eruditorum» — де өзінің дифференциалдық есептеулерінің әдістерін жариялап, df/dx белгілеуін енгізді. Ал, 1797 жылы Ж.Лагранж «туынды» (франц. «derivee») терминін енгізіп, туындыны y ', f ' белгілеулерімен белгілеуді ұсынды. Ғылым мен техника қарыштап дамыған заманда белгілі бір ұғымның бір салада ғана қолданылуы орынсыз болар еді. Себебі, ол ұғымдарды өзге салаларда қолданып көрсек, есептерді шешуде, жаңа техникалар ойлап табу барысында жетістіктерге жетуге көп көмегін тигізері сөзсіз. Осындай математиканың іргелі ұғымдарының бірі — туынды болып табылады. Туындыны тек алгебралық есептерді шешуде ғана емес, сонымен қатар жаратылыстану ғылымдарының өзге салаларында да, механикада, техникада, геометрияда қолдануға болады.
32.Көпжақтарды оқытудың мазмұны мен құылымы.
Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы – салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критериі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.Кеңістіктегі салу есептерін кластарға жіктеу туралы әр түрлі көзқарастар мен тәсілдер бар. А.Н. Чалов кеңістіктегі салу есептерін геометриялық салуды орындау тәсілдері бойынша келесі топтарға бөледі: 1) елестету арқылы шешілетін есептер; 2) проекциялық сызбамен шешілетін есептер; 3) модельмен шешілетін есептер. Салуға берілген стереометрия есептерін позициялық және метрикалық деп екі топқа бөлетіндер де бар. Негізгі элементтерінің қиылысуын ғана іздейтін, соны салумен аяқталатын есептер позициялық әдіспен шешілетін есептерге жатады. Кесінді салу, белгілі бір шамасы бар бұрышты салу, перпендикуляр тұрғызу, биссектриса жүргізу және т.б. белгілі шарттарды қанағаттандыратын фигура салу талабы қойылатын есептер метиркалық есептерге жатады. Мысалы, В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович өздерінің құрастырған «Математикалық есептер шешу практикумында» кеңістіктегі салуға берілген есептерді мынадай әдістер бойынша топтарға бөледі: 1) кеңістіктегі қарапайым салулар; 2) нүктелердің геометриялық орындары; 3) кейбір нүктелердің геометриялық орындары мен түзулерді пайдалану; 4) кескіндеу арқылы салу. Салуға берілген стереометрия есептері талдау, салу, дәлелдеу және зерттеу сияқты төрт кезеңнен тұрады.Талдау – бір бүтінді, құрамды бөліктерге жіктейтін, әр бөлікті жеке қарастыратын зерттеу әдісі. Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері: аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі. Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері: аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі. Проективтік әдіс (проекциялық сызбада салу есебін шешу әдісі). Егер ерекше проекциялау ережесі бойынша геометриялық денелердің кескінін пайдалануға мүмкіндік болса, онда ол есепті сызбалық құралдың көмегімен барлық салу жұмысын орындауға болады. Геометриялық орындар әдісі. Кеңістікте элементтердің геометриялық орындарын табуға берілген кез келген есепті салу есебі ретінде тұжырымдауға болады.
33-34. Көпжақтар.Көпжақ туралы ұғым. Стереометрмяда кеңістіктегі функцияларды дене деп атайды. Әрбір денені осы денеден тұратын және дене бетімен шектелген кеңістіктің бір бөлігі ретінде қарастыруға болады.Көпжақ деп беті саны шектеулі жазық көпбұрыштардан құралатын денені атайды. Егер көпжақ өзінің бетін құрайтын әрбір жазық көпбұрыш жазықтығының бір жағына орналасқан болса, оныдөңес көпжақ деп атайды.Дөңес көпжақтың беті мен оны шектейтін жазықтықтың ортақ бөлігі жақ деп аталады. Дөңес көпжақтардың жақтары дөңес көпбұрыштар болып келеді. Жақтардың қабырғаларын көпжақтың қырлары деп, ал төбелерін көпжақтың төбелері деп атайды. Ешбір жақта жатпайтын және көпжақтың кез келген екі төбесін қосатын кесінді көпжақтың диагоналы деп аталады.Көпжақ, үш өлшемді кеңістікте – бірнеше (шектеулі) жазық көпбұрыштан құрылған геометриялық бет. Көпжақ құрамындағы көпбұрыштың әрбір қабырғасы оған іргелес екінші көпбұрыштың да қабырғасы болып саналады. Ал әрбір көпбұрыштан іргелес көпбұрыштар арқылы кез келген көпбұрышқа өтуге болады. Жазық көпбұрыштарды көпжақтың жақтары деп, екі көпбұрыштың ортақ қабырғасын көпжақтың қырлары деп, ал көпбұрыштардың төбелерін көпжақтың төбелері деп атайды. Егер көпбұрыштың барлық төбесі кез келген жағы арқылы жүргізілген жазықтықтың бір жағында орналасса, онда оны дөңес көпжақ деп атайды.
Дұрыс көпжақтар . Егер көпжақ:1) дөңес болса;
2) Жақтары қабырғаларының саны бірдей көпбұрыштар болса;
3)Әрбір төбесінен шығатын қырларының саны бірдей болса, онда бұл көпжақ дұрыс деп аталады.
Дөңес дұрыс көпжақтардың бес түрі болады: куб (алты шаршыдан құралған),дұрыс тетраэдр (төрт дұрыс үшбұрыштан құралған), дұрыс октаэдр (сегіз дұрыс үшбұрыштан құралған дұрыс сегізжақ), додекаэдр (он екі дұрыс бесбұрыштардан құралған дұрыс он екі жақ), икосаэдр (жиырма теңқабырғалы үшбұрыштан құралған дұрыс жиырма жақ).Енді, осы көпжақтардың формулаларын көрсетейік. Ол үшін келесібелгілеулерді енгіземіз: V – көпжақтың көлемі, S – көпжақ бетінің ауданы, R –көпжаққа сырттай сызылған сфераның радиусы, r – көпжаққа іштей сызылған сфераның радиусы, h – қөпжақтың биіктігі (мағынасы болса), a – көпжақтың бір-біріне тең болатын әрбір қыры.
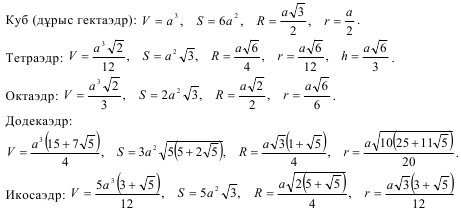
![]()
![]()
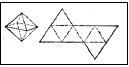
1-Куб және оның жазбасы 2- Дұрыс тетраэдр және оның жазбасы 3- Октаэдр және оның жазбасы


4- Додекаэдр және оның жазбасы 5- Икосаэдр және оның жазбасы
35. Цилиндр ,конус, шар,сфера ұғымдары.
Цилиндр деп бір жазықтықта жатпайтын, параллель көшіргенде дәл беттесетін екі дөңгелектен және осы дөңгелектердің сәйкес нүктелерін қосатын барлық кесінділерден құралатын денені айтады. Дөңгелектерді цилиндрдің табандары деп, ал дөңгелектер шеңберлерінің сәйкес нүктелерін қосатын кесінділерді цилиндрдің жасаушалары деп атайды. Параллель көшіру дегеніміз қозғалыс болғандықтан, цилиндрдің табандары тең болады. Егер цилиндрдің жасаушылары табан жазықтықтарына перпендикуляр болса, онда оны тік цилиндр деп атайды.Цилиндрдің радиусы деп оның табанының радиусын атайды. Цилиндрдің биіктігі деп табан жазықтықтарының ара қашықтығын атайды. Цилиндрдің осі деп табандарының центрлерінен өтетін түзуді атайды. Ол түзу жасаушаларға параллель болады. Конус деп дөңгелектен-конустың табанынан, бұл дөңгелектің жазықтығында жатпайтын нүктеден конустың төбесінен және конустың төбесін табанындағы шеңбердің нүктелерімен қосатын барлық кесінділерден құралған денені айтады.Конустың төбесін табанындағы шеңбердің нүктелерімен қосатын кесінділер конустың жасаушылары деп аталады.Конустың беті табаны мен бүйір бетінен құралады. Егер конустың төбесін табанының центрімен қосатын түзу табан жазықтығынаперпендикуляр болса,ол тік конус деп аталады. Конустың биіктігі деп оның төбесінен табан жазықтығына түсірілген перпендикулярды атайды.Тік конус биіктігінің табаны табанының центрімен дәл келіп беттеседі.Тік дөңгелек конустың осі деп оның биіктігін қамтитын түзуді атайды. Шар деп берілген нүктеден берілген қашықтықтан артық емес қашықтықта жататын кеңістіктің барлық нүктелерінен тұратын денеі айтады.Бұл нүкте шардың центрі деп, ал берілген ара қашықтық шардың радиусы деп аталады. Шардың шекарасы шардың беті немесе сфера деп аталады. Шар бетінің екі нүктесін қосатын және шардың центрінен өтетін кесінді диаметр деп аталады.Кез келген диаметрдің ұштары шардың диаметрлік қарама-қарсы нүктелері деп аталады. Шар да, цилиндр мен конус сияқты, айналу денесі болып табылады. Сфера (гр. sphaіra – шар), математикада – барлық нүктелері бір нүктеден (сфера центрінен) бірдей қашықтықта болатын тұйық бет. Сфера центрін оның кез келген бір нүктесімен қосатын кесінді (сондай-ақ оның ұзындығы) сфераның радиусы деп аталады.
36. Айналу денесі — қозғалмайтын оське қатысты жазық фигураны айналдырғаннан пайда болған дене. Цилиндр деп бір жазықтықта жатпайтын, параллель көшіргенде дәл беттесетін екі дөңгелектен және осы дөңгелектердің сәйкес нүктелерін қосатын барлық
кесінділерден құралатын денені айтады. Дөңгелектерді цилиндрдің табандары деп, ал дөңгелектер шеңберлерінің сәйкес нүктелерін қосатын кесінділерді цилиндрдің жасаушалары деп атайды.
 Параллель
көшіру
дегеніміз қозғалыс болғандықтан,
цилиндрдің табандары тең болады.
Параллель көшіргенде
жазықтық параллель жазықтыққа ауысады,
ендеше, цилиндрдің табандары параллель
жазықтықтарда жатады. Параллель
көшіргенде
нүктелер параллель түзулердің бойымен
бірдей ара қашықтыққа жылжитындықтан,
цилиндрдің жасаушылары параллель және
тең болады. Егер цилиндрдің жасаушылары
табан жазықтықтарына перпендикуляр
болса, онда оны тік цилиндр деп атайды.
Цилиндрдің радиусы деп оның табанының
радиусын атайды. Цилиндрдің биіктігі
деп табан жазықтықтарының ара қашықтығын
атайды. Цилиндрдің осі деп табандарының
центрлерінен өтетін
түзуді атайды. Ол түзу жасаушаларға
параллель болады.
Параллель
көшіру
дегеніміз қозғалыс болғандықтан,
цилиндрдің табандары тең болады.
Параллель көшіргенде
жазықтық параллель жазықтыққа ауысады,
ендеше, цилиндрдің табандары параллель
жазықтықтарда жатады. Параллель
көшіргенде
нүктелер параллель түзулердің бойымен
бірдей ара қашықтыққа жылжитындықтан,
цилиндрдің жасаушылары параллель және
тең болады. Егер цилиндрдің жасаушылары
табан жазықтықтарына перпендикуляр
болса, онда оны тік цилиндр деп атайды.
Цилиндрдің радиусы деп оның табанының
радиусын атайды. Цилиндрдің биіктігі
деп табан жазықтықтарының ара қашықтығын
атайды. Цилиндрдің осі деп табандарының
центрлерінен өтетін
түзуді атайды. Ол түзу жасаушаларға
параллель болады.
Цилиндрді жазықтықтармен қию
Цилиндрді осіне параллель жазықтықпен қиғанда қимасы тік төртбұрыш болып шығады.Оның екі қабырғасы-цилиндрдің жасаушылары, ал қалған екеуі табандарының параллель хордалары болады.Дербес жағдайда, остьік қима тік төртбұрыш болып табылады. Бұл-цилиндрдің осі арқылы өтетеін жазықтықпен қиғандағы қима.
Цилиндрдің табанына параллель жазықтық оның бүйір бетін табан шеңберіне тең болатын шеңбер бойымен қиып өтеді.
Шар деп берілген нүктеден берілген қашықтықтан артық емес қашықтықта жататын кеңістіктің барлық нүктелерінен тұратын денеі айтады.Бұл нүкте шардың центрі деп, ал берілген ара қашықтық шардың радиусы деп аталады
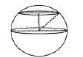 Шардың
шекарасы шардың беті немесе сфера деп
аталады.
Шардың
шекарасы шардың беті немесе сфера деп
аталады.
Шар бетінің екі нүктесін қосатын және шардың центрінен өтетін кесінді диаметр деп аталады.Кез келген диаметрдің ұштары шардың диаметрлік қарама-қарсы нүктелері деп аталады.
Шар да, цилиндр мен конус сияқты, айналу денесі болып табылады.Ол жарты дөңгелекті ось ретінде диаметрден айналдырғанда шығады.
Шарды жазықтықпен қию
Шарды жазықтықпен қиғандағы кез келген қимасы дөңгелек болады.Бұл
дөңгелектің центрі шардың центрінен қиюшы жазықтыққа түсірілген перпендикулярдың табаны болып табылады.
Конус деп дөңгелектен-конустың табанынан, бұл дөңгелектің жазықтығында жатпайтын нүктеден конустың төбесінен және конустың төбесін табанындағы шеңбердің нүктелерімен қосатын барлық кесінділерден құралған денені айтады.Конустың төбесін табанындағы шеңбердің нүктелерімен қосатын кесінділер конустың жасаушылары деп аталады.Конустың беті табаны мен бүйір бетінен құралады.
Егер конустың төбесін табанының центрімен қосатын түзу табан жазықтығына перпендикуляр болса,ол тік конус деп аталады.
Конустың биіктігі деп оның төбесінен табан жазықтығына түсірілген
перпендикулярды атайды.Тік конус биіктігінің табаны табанының центрімен дәл келіп беттеседі.Тік дөңгелек конустың осі деп оның биіктігін қамтитын түзуді атайды.
 Конустың
жазықтықтарымен қиғандағы қималары
Конустың
жазықтықтарымен қиғандағы қималары
Конустың төбесі арқылы өтетін жазықтықпен қиғанда қимада бүйір
қабырғалары конустың жасаушылары болып табылаиын, тең бүйірлі үшбұрыш шығады.Дербес жағдайда,конустың осьтік қимасы тең бүйірлі үшбұрыш болады.Осьтік қима конустың осі арқылы өтеді.
Конустың табан жазықтығына параллель жазықтық конусты дөңгелек
бойымен, ал бүйір бетін центрі конустың осьінде жататын шеңбер бойымен
қиып өтеді.
37.Айналу
денелерінің көлемі және беті.Айналу
осьтері, әсіресе дөңгелек фигураларда
–сферада, шарда, цилиндірде , конуста
болады. Сондықтан оларды айналу денелеріде
деп атайды. «Цилиндр»
сөзі ол гректің kulindros сөзінен алынған,
ол «валик» -«оқтау» мағынасын
білдіреді.Радиусы R-ге тең және биіктігі
h-қа тең цилиндрдің көлемін анықтау үшін
Oxyz тік бұрышты координаталар жүйесін
(1) -суретте көрсетілгендей етіп аламыз.
Онда цилиндрдің [0;h] аралығындағы көлденең
қимасының ауданы хϵ[0;h] нүктесін таңдап
алуымызға тәуелсіз, тұрақты болады,
яғни ол цилиндірдің табан ауданы ![]() –қа тең. Сондықтан цилиндірдің көлемі
былай анықталады:V=
–қа тең. Сондықтан цилиндірдің көлемі
былай анықталады:V=![]() =
=![]()

(1-сурет) (2)-сурет
Сонымен, цилиндірдің көлемі табаны ауданын биіктігіне көбейткенге тең: V= .
Конустың көлемі .Биіктігі һ-қа және радиусы R-ге тең конусты (2)-суретте көрсетілгендей етіп орналастырамыз. хϵ[0;h] нүктесінде жүргізілген та банына параллель қимасының ауданы S(х)-ті R,һ және х арқылы өрнектейік. ОР= R, ОР=һ, ОО1 = х болғандықтан РО1В және РОА тік бұрышты үшбұрыштардың ұқсастығынан

Теңдігін
аламыз . Онда

Сондықтан
![]() Сонымен,
конустың көлемі табан ауданы мен биіктігі
көбейтіндісінің 1/3 бөлігіне тең:
Сонымен,
конустың көлемі табан ауданы мен биіктігі
көбейтіндісінің 1/3 бөлігіне тең:

Табан радиустары R-ге және r-ге,ал биіктігі h-қа тең қиық конустың көлемі (96 -сурет)
![]() .Формуласымен
анықталады. Бұл формула сәйкес қиық
пирамида көлемінің формуласы сияқты
дәлелденеді.
.Формуласымен
анықталады. Бұл формула сәйкес қиық
пирамида көлемінің формуласы сияқты
дәлелденеді.
Шар
көлемі .Шардың
центірі арқылы өтетін жазықтық оның
симметрия жазықтығы болңандықтан,
алдымен жарты шар көлемін анықтап, оны
екі еселесек, жеткілікті. Радиусы R-ге
тең жарты шарды 97-суретте көрсетілгендей
етіп орналастырамыз.S (х) қимасы ауданы
х-ке (xϵ[0;R]) тең тәуелді функция болады.
Енді осы функцияны анықтайық. ОА=R=OB,
OC=x болғандықтан, қима
радиусы CB=![]() теңдігімен
анықталады. Осыдан қима ауданы S(x)=
теңдігімен
анықталады. Осыдан қима ауданы S(x)=![]() -қа тең. Олай болса жарты шар көлемі
-қа тең. Олай болса жарты шар көлемі
 теңдігімен,
ал шар көлемі
теңдігімен,
ал шар көлемі
 формуласымен
анықталады.
формуласымен
анықталады.
38. Үшбұрыштар Үшбұрыштардың теңдік белгілері I белгі. Егер бір үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы сәйкесінше екінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышына тең болса, онда мұндай үшбұрыштар тең болады. II белгі. Егер бір үшбұрыштың бір қабырғасы мен оған іргелес бұрыштары
сәйкесінше екінші үшбұрыштың бір қабырғасы мен оған іргелес бұрыштарына тең болса, онда мұндай үшбұрыштар тең болады. III белгі. Егер бір үшбұрыштың үш қабырғасы сәйкесінше екінші екінші үшбұрыштың үш қабырғасына тең болса, онда мұндай үшбұрыштар тең
болады. Егер үшбұрыштың екі қабырғасы тең болса, ол тең бүйірлі үшбұрыш деп аталады. Бұл тең қабырғалар үшбұрыштың бүйір қабырғалары деп ,ал үшінші қабырғасы үшбұрыштың табаны деп аталады. Тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болады.
Барлық қабырғалары тең болатын үшбұрыш тең қабырғалы үшбұрыш деп аталады. Егер үшбұрыштың екі бұрышы тең болса, онда ол тең бүйірлі болады. Үшбұрыштың берілген төбесінен түсірілген биіктігі деп осы төбеден үшбұрыштың қарсы жатқан қабырғасын қамтитын түзуге жүргізілген перпендикулярды айтады. Үшбұрыштың берілген төбесінен жүргізілген биссектрисасы деп үшбұрыш бұрышының биссектрисасының осы төбені қарсы жатқан қабырғадағы нүктемен қосатын кесіндісін айтады. Үшбұрыштың берілген төбесінен жүргізілген медианасы деп осы төбені қарсы жатқан қабырғаның ортасымен қосатын кесіндіні айтады. Тең бүйірлі үшбұрыштың медианасының мынадай қасиеті бар: Теңбүйірлі үшбұрыштың табанына жүргізілген медианасы оның биссектрисасы да, биіктігі де болып табылады.
