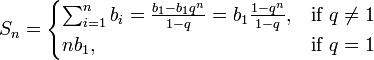23.Мектеп курсы математиксында теңдеулер мен теңсіздіктерді және олардың жүйесін оқыту әдістемесі.

Теңдеулер мен теңсіздіктерге байланысты материалдар мектеп курсы

математикасының мазмұнының қомақты бөлігін құрайды, себебі теңдеулер

мен теңсіздіктер математиканың түрлі салаларында және маңызды

қолданбалы есептерді шығаруда кең қолданыс табады. Сондықтан да

оқушыларды теңдеулер мен теңсіздіктер желісінің қолданбалық, теориялық-

математикалық және математика курсының басқа да мазмұндық желілермен

байланысын құру бағыттарын игерту мәселесі теңдеулер мен теңсіздіктерді

шешуге үйрету материалдарын талдау мен синтездеу деңгейінде саналы

игерту мәселесімен тығыз байланысты.

Математиканы дәстүрлі оқыту жүйесінде теңдеулер мен теңсіздіктерді

оқытудың нәтижелеріне талдау жасау келесідей кемшіліктердің бар екеніне

көз жеткізді:

- Оқушылардың теңдеулер мен теңсіздіктерді шешу әдістерін игеру

барысында олардың қолданыс табуының болашағын болжай алмайтындығын;

- теңдеу мен теңсіздіктерді шешу әдістерінің біртұтас жүйе екендігіне

көзқарастың қалыптаспайтындығын;

- теңдеулер мен теңсіздіктер шешу әдістерінің математиканың негізгі

желілер мазмұнымен байланысын күшейтетініне көздерінің жете

бермейтіндігін;

- теңдеулер мен теңсіздіктерді шешу әдістерін бағытты игертуге терең

мән берілмейтіндігін т.с.с. Бұл кемшіліктер қазіргі таңда оқушылардың

математикаға деген қызығушылығының төмендеуінің бірден – бір себебі деп

айтуға болады.Теңдеулер мен теңсіздіктер теориясы орта мектепте оқушылардың логикалық ойлау қабілетін дамыта алатындай, өз алдына ғылыми-педагогикалық маңызы бар негізгі оқу материалы болып есептеледі. Ол оқушыларды айқын дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады. Теңдеулер мен теңсіздіктерді оқыту кезінде оқытушының өзінің баяндауы мен көрнекілікті үйлестіруі елеулі роль атқарады.Теңдеулер мен теңсіздіктерді оқытудың тиімділігін арттыру жолдарының бірі - графиктерді пайдалану болып табылады.

«Сызықтық теңдеулер жүйелері» тақырыбында қарастырылатын сызықтық теңдеулер жүйелерін шешудің ауыстыру және қосу тәсілдеріне сәйкес жүйені шешудің екі алгоритмі болады. Осы

алгоритмдер бірінен кейін бірі орындалатын қарапайым амалдар ретінде

ауызша айтылады.

Сызықтық теңдеулер жүйесін ауыстыру тәсілімен шешу үшін:

1) жүйенің бір теңдеуіндегі айнымалының бірі екіншісі арқылы

өрнектеледі; 2) екінші теңдеудегі айнымалының орнына алынған өрнек

қойылады; 3) шыққан бір айнымалысы бар теңдеу шешіледі; 4)

айнымалының мәні (1) пунктте шыққан өрнектегі орнына қойылады; 5)

өрнектің сандық мәні, яғни екінші айнымалы табылады; 6) (3) және (5)

пункттерде шыққан сандар жүйенің шешімі болады. Сызықтық теңдеуді қосу тәсілімен шешу үшін: 1) айнымалылардың коэффициенттері салыстырылады; 2) егер бір айнымалының коэффициенттері қарама қарсы сандар болса, онда осы алгоритмнің (4) пункті орындалады, болмаса келесі пункттегі нұсқау орындалады; 3) теңдеулердің әрқайсысының барлық мүшелерін сәйкес бір санға көбейту арқылы айнымалылардың біреуінің коэффициенттері қарама-қарсы сандарға келтіріледі; 4) алынған теңдеулердің сол жақ және оң жақ сәйкес бөліктері мүшелеп қосылады; 5) шыққан бір айнымалысы бар тендеу шешіліп, айнымалының мәні табылады; 6) айнымалының мәні жүйенің кез келген теңдеуіне қойылады; 7) шыққан бір айнымалысы бар теңдеудің түбірі табылады; 8) 5 және 7 пункттерде табылған айнымалылардың мәндері жүйенің шешімі болады.

Теңдеулер мен теңсіздіктерді оқыту кезінде оқытушының өзінің баяндауы мен көрнекілікті үйлестіруі елеулі роль атқарады.Теңдеулер мен теңсіздіктерді оқытудың тиімділігін арттыру жолдарының бірі - графиктерді пайдалану болып табылады.

24.Тізбекті және оның шегін оқыту әдістемесі. Мүшелерін нөмірлеп шығуға болатын шексіз сандар жиынын сан тізбегі деп атаймыз.Тізбекті құрайтын сандар рет ретімен, тізбектің бірінші, екінші, үшінші,т.с.с.мүшелері деп аталады.Тізбектің мүшелерін , әдетте оның реттік нөмірін көрсететін индекстері бар әріптермен белгілейді: _{Тізбектің n мүшесін оның жалпы мүшесі деп атайды және оны арқылы, ал тізбектің өзін қысқаша арқылы белгілейді. Жалпы, сан тізбегін әр түрлі тәсілдермен анықтауға болады. Бұл тәсілдердің ең қолайлы және жиі қолданылатыны -ол тізбектің n- мүшесінің формуласымен анықтау, яғни тізбектің кез келген мүшесін өрнектейтін формула арқылы анықтау .Мысалы:}

1) 1, …..,

3) 0, 1, 0, 0, …;

4) x _n =(-1) ; -1, 1, -1, 1…;

5) x _n=1; 1; 1, 1, …;

Кейде тізбектің әрбір мүшесін оның алдыңғы мүшелері арқылы анықтайды, бұл тәсілді рекуренттік деп атайды. Мысалы: аn= аn-1+аn-2 (п=3,4,...), яғни 1, 1, 2, 3, 5, 8, .... – бұл тізбек Фибоначчи тізбегі деп аталады. Тізбектің мүшелерін сөзбен де сипаттап беруі мүмкін. Сан тізбегін бірінен соң бірін тізіп жаза салған сандар жиыны деген қате түсінік қалыптаспауы үшін оның функция екенін тағы да естеріңізге сала кетейік, бір сөзбен айтқанда оның мүшелерін анықтайтын ереже берілуі керек.

Бірсарынды тізбектер.Егер _{сан тізбегі үшін оның екінші мүшесінен бастап әрбір мүшесі алдыңғы мүшесінен артық болса ,онда мұндай тізбекті өспелі тізбек деп атаймыз. Ал егер оның әрбір мүшесі келесі мүшесінен артық болса ,онда мұндай тізбекті кемімелі тізбек деп атайды. Жалпы өспелі және кемімелі, кемімейтін және өспейтін тізбектерді бір атпен бірсарынды тізбектер деп атаймыз. Мысалы: 2, 4, 6, 8 ,2n тізбектері өспелі тізбектер ал ,} 1, ….., _{тізбектері кемімелі тізбектер. Егер А саны табылып тізбегінің әрбір мүшесі үшін}

_{>А теңсіздігі орындал тізбегін төменнен шенелген деп атаймыз.Ал қандай да бір В саны табылып} <В теңсіздігі орындалса онда тізбегі жоғарыдан шенелген деп атаймыз. Егер тізбек әрі төменнен әрі жоғарыдан шенелген болса , яғни А және В сандары табылып тізбегінің әрбір мүшесі үшін А< <В теңсіздігі орындалса онда бұл тізбекті шенелген деп атаймыз. Ал енді сан тізбектерінің шегінің анықтамасын қарастырайық. 1- анықтама. Егер санға белгілі бір ереже (заң) бойынша нақты саны сәйкестендірілсе, онда сан тізбегі немесе жай тізбек берілген дейді.

Тізбекті символдарының біреуімен белгілейді.

2- анықтама. Егер кез келген санына сәйкес N=N( ) саны табылып, үшін теңсіздігі орындалса, а санын тізбегінің шегі деп атайды да оны былай жазады: 3- анықтама. Егер тізбек шегі саны тиянақты (шекті) сан болса, онда оны а санына жинақты дейді. 4- анықтама. Егер тізбектің шегі жоқ немесе болса, онда ол тізбекті жинақсыз дейді. 1-теорема. Жинақты тізбектің тек бір ғана шегі бар.2-теорема. Кез келген жинақты тізбек шектелген. Ескерту. Кез келген шектелген тізбек жинақты деуге болмайды. Шектің негізгі қасиеттері Теорема 1.

Егер Тізбегінің шегі бар болса онда ол шек жалғыз болады Теорема 2.

Тұрақты санның шегі өзіне тең =C Теорема 3. Қосындының шегі шектердің қосындысына тең + Теорема 4. Тұрақты көбейткішті шек таңбасы алдына шығаруға болады =k Теорема 5.Көбейтіндінің шегі шектердің көбейтіндісіне тең = * Теорема 6. Бөлімінің шегі нөлден өзгеше болғанда бөліндінің шегі шектердің бөліндісіне тең = / Теорема 7. Дәреженің шегі шектердің дәрежесіне тең

) Ескерту Бұл тұжырымдардағы қарастырылған әрбір тізбектің шегі бар деп есептелінеді Мысал 1. тізбегінің шегі =0 болатынын дәлелде.

Кез келген >0 санын алып теңсіздігі n – нің қандай мәндерінде орындалатынын анықтаймиыз. Сол мақсатпен 1) теңсіздігін n - ге қарай шешеміз: Онда болғанда (1) орындалатынын көреміз. Мысал 2 тізбегінің шегі жоқ.

Шынында, бұл тізбек -1, 1, -1, 1,… (2)белгілі. Кері жорып (2) тізбектің шегі а саны бар дейік.Онда (мысалы ) үшін N нөмері табылып орындалады. х_n=1 болғандықтан және болады.

Олай болса Бұл қайшылық (2) тізбек жинақты дегеніміздің дұрыс емес екенін көрсетеді. теорема. Егер {x_n}, {y_n} тізбектері жинақты және , болса, онда {x_n y_n} тізбегі жинақты, lim(x_n y_n) = a b. n

1. {x_n y_n} тізбегі жинақты, lim(x_n y_n) = a b.

n

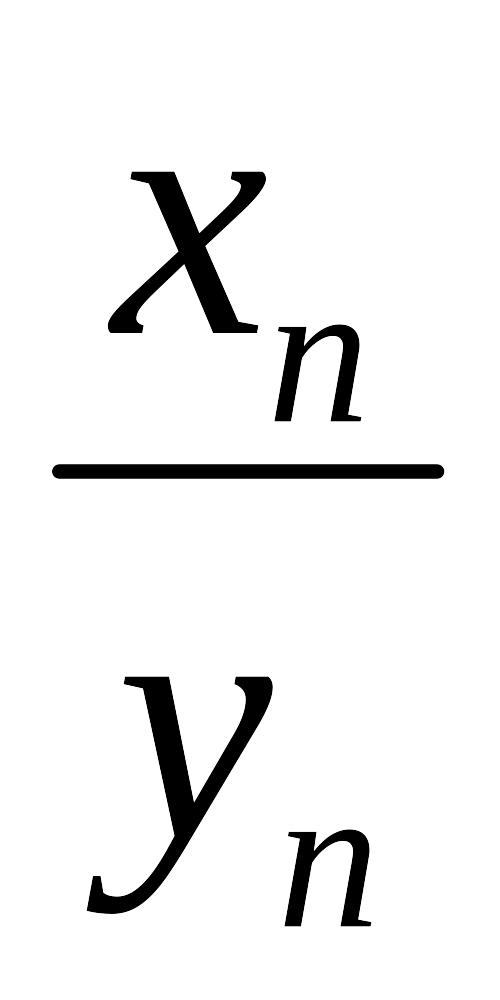2. { }, b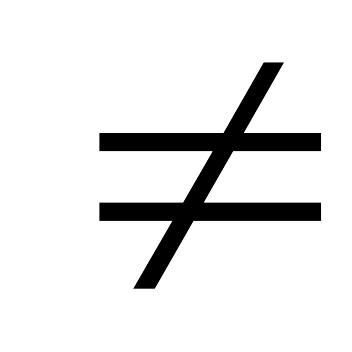 0 тізбегі жинақты, lim =

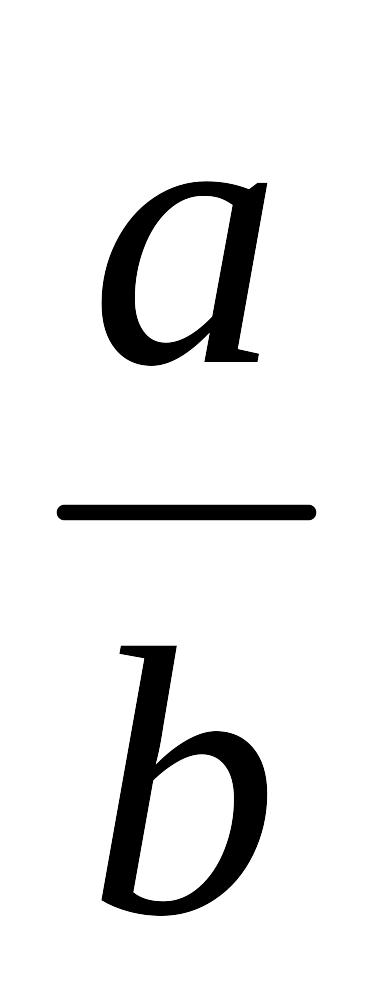
n болады.

25. Математика курсында прогрессияларды, қарапайым сандық қатарларды оқыту. Арифметикалық прогрессия , 1-реттік арифметикалық қатар — әрбір келесі саны (2-саннан бастап) алдыңғысына бір тұрақты d санын қосқанда шығатын сандар тізбегі.

d саны арифметикалық прогрессияның айырмасы деп аталады. Сонымен әрбір арифметикалық прогрессия мына түрде жазылады:

Арифметикалық прогрессияның жалпы мүшесі

формуласымен өрнектеледі. Арифметикалық прогрессияның жалпы мүшесінің тағы бір қасиеті мынадай: . Егер d>0 болса, онда арифметикалық прогрессия өспелі, егер d<0 болса, онда кемімелі болады. Арифметикалық прогрессияның ең қарапайым мысалына натурал сандар тізбегі жатады. Арифметикалық прогрессия мүшелерінің саны шектелген не шектелмеген болуы мүмкін. Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы

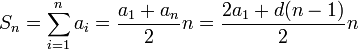 формуласы арқылы есептеледі.

Геометриялық прогрессия — әрбір мүшесі (екіншісінен бастап) алдыңғы мүшесінен қандай да бір еселік деп аталатын тұрақты санға ( ) көбейтуден шығатын сан қатары :  . Геометриялық Прогрессия q>1 болса, өспелі Геометриялық Прогрессия, 0<q<1 болса, кемімелі Геометриялық Прогрессия, ал q<0 болса, ауыспа таңбалы Геометриялық Прогрессия деп аталады. Геометриялық Прогрессияның кез келген мүшесі (b_k) бірінші мүшесі (b₁) мен еселігі (q) арқылы мына формуладан табылады: :  . Ал Геометриялық Прогрессияның (еселігі 1-ге тең емес) алғашқы n мүшесінің қосындысы (S_n) мына формула бойынша анықталады:

• 

Егер |q|<1 болса, және мүше саны (n) шексіз өссе, онда Sn қосындысы шегіне ұмтылады. Осы S саны шексіз кемімелі геометриялық прогрессияның қосындысы деп аталады. а1+а1q+...+а1qn+... (|q|<1 болғанда) өрнегі геометриялық қатар деп аталатын жинақты қатардың қарапайым мысалы болып есептеледі. Мұндай геометриялық қатардың қосындысы мынаған тең:

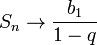•  егер 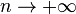  . Оң мүшелерден тұратын Геометриялық Прогрессияның кез келген мүшесінің мынадай қасиеті бар: .

26.IX сыныпта функцияның шегі ұғымын енгізу туралы. Орта мектеп математика бағдарламасына зер салып қарап шыққан әрбір адам, оқушы өзінің математикалық білім алу барысында ұғымдарды меңгерудің барлық кезеңдерін тездетілген қарқынмен өтіп шығатынын байқайды, ал кейбір ұғым өте ұзақ және қиындықпен қалыптастасқан болса, онда қазіргі оқушылар да оны сондай қиындықпен меңгеретініне таң қалмас еді. Сондықтан көптеген оқытушылар жаңа ұғымды оқушы дұрыс қабылдауы үшін оны берудің аз да болса жеңілдетілген жолын, әдісін іздейді. Соның бірі ретінде біз мектеп математика курсында шек ұғымын енгізу мәселесін қарастырайық. Жоғары математиканың классикалық оқулықтарында шекті алдымен тізбектер үшін, содан кейін функция үшін енгізеді. Осы әдіс көптеген жылдар бойы сынақтан өткені тәжірибесі мол әдіскер-оқытушыларға белгілі. Классикалық оқулықтар авторлары да белгілі бір тәжірибелерге сүйене отырып осы әдісті таңдаған болу керек, себебі мектеп оқулығымен оқып келген бірде-бір студенттің шекті түсініп келгенін осы уақытқа дейін кездестірген емеспіз.

Ал орта мектепте қолданыста жүрген оқулықтарда шек ұғымын бірден функция үшін береді,

бірақ шек ұғымы туралы сөз болмай тұрып функцияның үзіліссіздігіне анықтама береді де, осы

анықтамада шекті белгілеу мен «ұмтылады» деген сөзді қолданады. Осы уақытқа дейін мектеп

оқулықтарында шек ұғымын берудің әртүрлі әдістері қарастырылды, соның бірі формальді

анықтамасын бірден тұжырымдау болып табылады. Мұндай әдісті қолдануда шек ұғымының

негізгі идеясын оқушылардың санасына жеткізу өте қиынға түседі. Себебі анықтамада

процестердің саны көп, аргумент пен функцияның ұмтылыстары екі процесс, оның үстіне ε

мен δ сандары тосыннан пайда болған сияқты болып көрінеді, олардың бір-бірімен байланысу

нәтижесінде ұғым күрделеніп, қорытындысында оқушылардың мұндай пайымдауларды

қабылдауға мүмкіншіліктері жете бермейді

Ал, енді мектеп оқулығына функция шегінің енгізілуі туралы айтатын болсақ...

Жоғарыда атап өткеніміздей, қолданыста жүрген оқулықтардағы сияқты функцияның

үзіліссіздігі тақырыбына көшпей тұрып, функцияның дербес жағдайы болатын тізбек үшін

«ұмтылады» деген сөздің мағынасын ашып алғаннан кейін ғана функция жағдайына көшуге

болады деп есептейміз. Себебі функция үшін «ұмтылады» деген сөздің өзі екі жерде (аргументтің

және функцияның мәндерінің ұмтылуы) қолданылады. Мектепте қазіргі қолданыста жүрген [2,91] 10 сынып оқулығында функция шегінің анықтамасы былай берілген: «х аргументі ұмтылатын а мәні ƒ(х) функциясының анықталу облысының ішінде жатса, онда функцияның сол нүктедегі мәні оның

шектік мәні болып табылады, яғни а саны функцияның анықталу облысына тиісті болса, онда

lim f (x) = f (a) »

x → a

Бұл анықтаманың дұрыс еместігін бір мысал

арқылы ғана көрсетуге болады, мұнда ƒ(0)=0, яғни функция бұл нүктеде анықталған, ал бірақ

lim f (x) = 1

x → 0

Сондықтан мұғалімге бұл мәселені шешу үшін оның ең болмағанда көрнекілік деңгейдегі әдісін қолданып, оқушыға жеткізе алатындай жолмен баяндауды (біздің қалыптасқан жағдайларда мұғалім оқулықтарда тақырып қалай берілді, сабақта да дәл солай бере салады) қажет етеді..

Енді тізбек шегінің геометриялық үлгісіне сүйене отырып, функцияның шексіздіктегі

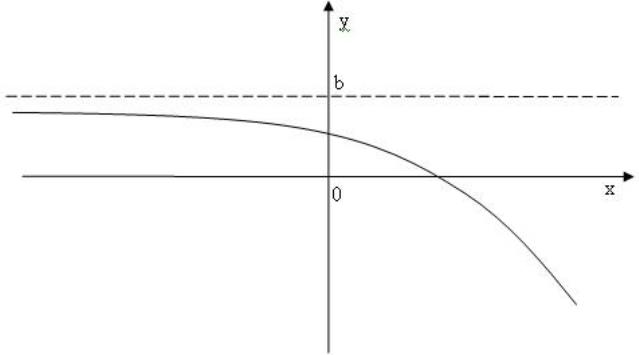
шегінің анықтамасын беруге тырысайық. Мектепте функция шегінің формальді анықтамасын берудің қажеті жоқ, оны функцияны зерттеу барысында жиі қолданатын шексіздіктегі шегінен бастау керек. Функция шегіне мұндай жолмен келу дидактикалық пайымдауларға байланысты.Оқушылар асимптота ұғымын мектеп математикасында пайдаланып келеді, яғни горизонталь асимптота функцияның шексіздіктегі шегінің, ал вертикаль асимптота нүктенің маңайында функцияның өзінің мәні шексіз өсуінің немесе кемуінің геометриялық үлгісі(моделі) болып табылады. Функция графигінің эскизі сурет-5 пен сурет-6-дағыдай жағдайларды қарастырайық. Функцияның бұл геометриялық моделі-функция аргументі шексіз өскенде оның мәндері у=b түзуіне жақындай беретінін көрсетеді. Ал математикада ыңғайлы болу үшін осы геометриялық модельдің аналитикалық аналогін жазу қалыптасқан. Оны былай жазады:

lim f (x) = b және lim f (x) = b (1)

x →- ∞ x →+ ∞

Оны «функцияның плюс шексіздіктегі шегі» және «функцияның минус шексіздіктегі шегі»

дейді. Ал сурет-7 жағдайындағы геометриялық модельді

lim f (x) = b (2)

x →∞

деп белгілеп, оны «функцияның шексіздіктегі шегі» деп атайды. Бұл суреттердегі у=b түзуін

функция графигінің горизонталь асимптотасы деп атайды.

Осындай көрнекілік деңгейіндегі шексіздіктегі шекпен танысқаннан кейін оқушы өзі (1)-(2)

теңдіктердің геометриялық моделіне, керісінше геометриялық моделінен олардың аналитикалық

өрнектеріне көше алатындай болуы, яғни функция графигінің горизонталь асимптотасын таба

алуы керек.

Маңайлардың 2-кестені пайдаланып (1)-(2) теңдіктер арқылы белгіленген шектердің

қатаң түрдегі анықтамасын беруге болады. Мұнда ұмтылу екі жерде айтылып тұрғандықтан,

аргумент туралы сөз болғанда оның ұмтылатын шегінің δ- маңайы деп, ал функция шегі болатын

санның(нүктенің) ε-маңайы деп белгілеу қабылданған. Шексіздіктегі шектерді қарастырып

отырғандықтан функцияның Х анықталу жиынына (а, +¥) және (-¥, d) түріндегі аралықтар

кіретін болсын деп келісіп алайық. Теңдік (1)-дегі бірінші жазудың анықтамасын беру үшін ε>0

санын алайық, ал функция b-санына ұмтылады деген ƒ(х)-тің мәндері b-ның ε-маңайында

жатуы керек. Ал бұл кестеде |ƒ(х)- b |< ε теңсіздігі арқылы өрнектеліп тұр, ендеше осы теңсіздікті

функция b-санына ұмтылады дегеннің орнымен алмастыруға болады. Одан әрі бұл теңсіздіктегі

ƒ(х)-тің мәндері қандай х-тің мәндері үшін алынып тұрғаны х +μ-ке ұмтылады деген ақпараттан

және кесте 2-ден х >δ(ε) теңсіздігі түрінде бейнеленеді. Осы айтылғандарды анықтама түрінде

тұжырымдайық:

А н ы қ т а м а 3. Егер белгілі бір b саны мен кез-келген ε>0 саны үшін х >δ(ε) теңсіздігін

қанағаттандыратын барлық хÎХ сандары үшін

|ƒ(х)- b |< ε теңсіздігі орындалатын δ(ε) >0 саны табылса, онда b санын ƒ(х) функциясының

х +¥-ке ұмтылғандағы шегі деп атайды.

Қалған (1)-(2) теңдіктер арқылы белгіленген шектердің де анықтамаларын осылайша

өрнектеп көрсетуге болады. lim f (x) = b

x →∞ дегеннің анықтамасын бергенде, анықтамада 3-те

х >δ(ε) теңсіздігін х < -δ(ε) теңсіздігіне, ал . lim f (x) = b

x →∞ дегенді өрнектеу үшін х >δ(ε) теңсіздігін

|х| > δ(ε) теңсіздігіне алмастыру керек

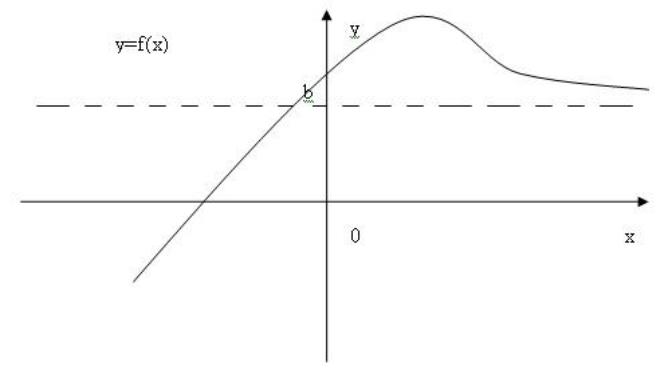
5-сурет 6-сурет

7-сурет 8-сурет

Енді белгілі бір нүктенің маңайында функция мәні шексіз өсетін не кемитін жағдайларды

қарастырайық. Көрнекілік үшін мысал қарастырудан бастайық.

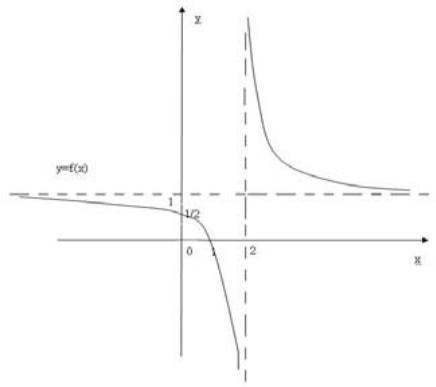
М ы с а л 4. f (x) =(x-1)/(x-2) функция туралы аз ғана ақпарат бойынша оның графигінің

эскизін салуға болады.

1) (-μ;2)È(2;+μ) жиынында анықталған;

2) кез келген хÎ(-μ;1)È(2;+μ) үшін f (x)>0, ал әрбір хÎ(1;2)

үшін f (x)<0;

3) у=1 түзуі оның горизонталь асимптотасы, яғни . lim (x-1)/(x-2)=1 және lim (x-1)/(x-2)=1

x →-∞ x →+∞

Бұл функция х=2 нүктесінде анықталмаған, сондықтан осы нүктенің маңайында зерттейік.

Аргументке (2;+μ) аралығынан мән бере отырып, яғни х=2 нүктесіне оң жағынан жақындай

берсек, функция мәні шексіз өсетінін көреміз, мұндай жағдайда функция(бұл аралықта

функция мәні оң) +μ-ке ұмтылады дейді, және оны lim f (x) = +∞

x →2+0 деп жазады. Дәл

осы сияқты аргументке (-μ;2) аралығынан мән бере отырып, х=2 нүктесіне сол жағынан

жақындай берсек, функция мәні шексіз кемиді(бұл маңайда функция мәні теріс). Осы жағдайды

оны lim f (x) = -∞

x →2-0 деп белгілеп, аргумент 2-ге сол жағынан ұмтылғанда, функция -μ-ке ұмтылады

дейді. Қарастырылған мысалда х-тің мәні 2-ге жақындағанда функция графигі х=2 түзуіне

жақындайтынын көрсетеді, неғұрлым х осы нүктеге жақын мән қабылдаса, солғұрлым функция

графигі х=2 түзуіне жақындай түсетінін көреміз(сурет 8-ді қараңыз). Осы зерттеулер мен

функцияның 1)-3) қасиеттерін пайдаланып, сурет 8-дегідей графиктің эскизін аламыз.

Осы мысалдан кейін вертикаль асимптота анықтамасын берейік .

А н ы қ т а м а 4. Егер оны lim f (x) = +∞ (не -μ) немесе lim f (x) = -∞ (не +μ)

x →x0+0 x →x0-0 болса, онда х=х0 түзуін ƒ(х) функциясы графигінің вертикаль асимптотасы атайды.

Ендеше, мысал 4-те х=2 түзуі берілген функцияның вертикаль асимптотасы болып

табылады. Осы мысалдан функцияның шегі арқылы оны зерттеу көп жеңілдейтінін көріп

отырмыз.

Мектеп математикасында функцияның шегін табу мақсат етіп қойылмаған, оны функцияны

зерттеу барысында асимптотасын тауып графигін салу үшін қолдану өте ыңғайлы. Себебі

функцияның туындысы ұғымын бермей тұрып 9 сыныпта рационал функцияларды зерттеу,

олардың графигін салу сияқты тақырыптар қарастырылады. Сол себеппен функция шегін

аргумент шексіз өсетін не кемитін және функцияның мәні шексіз өсетін не кемитін нүктелердегі

шектерді ғана қарастыру жеткілікті деп ойлаймыз.

Қалған көптеген жағдайлардың барлығы дерлік жоғары математика курсында егжей-

тегжейлі қарастырылады.

Біздің мақсатымыз бір жағынан неғұрлым үнемді түрде, екінші жағынан солғұрлым тақырыптың барлық маңызды мазмұнын қамтамасыз ете алатындай жаңа ұғымды ашу және оны

оқушыға нақты қабылдай алатындай етіп жеткізу, аталған тақырыптың әдістемелік мәселелерін

дамыта отырып өңдеп, мұғалімге дәл де, айқын теориялық әдістемелік нұсқауын беру болып

табылады. Сонымен орта мектепте оқушылардың жас ерекшеліктері мен математикалық білім

деңгейін ескере отырып, шектің қатаң анықтамасын бірден бере салудан бас тартып, алдымен

оның жеңілдеу түрі болатын интуитивті-көрнекілік тәсіл арқылы беруді ұсынамыз. Әрине,

соңында бәрін қорытындылай келе қазіргі дәуірдегі оқулықтардағыдай оның анықтамасын

тұжырымдауға болады.

Осы айтылғандарды ескере отырып, мектеп математикасында функция шегінің анықтамасын беру

үлгісін төмендегі ретпен берген бәрінен де ыңғайлы болады деген ойдамыз:

1.Тізбектің анықтамасын функцияның дербес жағдайы ретінде тұжырымдау, оның берілу

тәсілдеріне нақты мысалдар келтіріп, жан-жақты талдау, нөмірлері өскендегі тізбек мүшелерінің

өзгерісін зерттеу;

2.Тізбекті сан өсінде бейнелеп, оның нөмері өскендегі бет алысын (бағытын) көрнекі түрде,

ал кесте арқылы оның мәндерінің өзгеруін дәл көрсетіп, қорытынды жасау;

3. Алдыңғы көрнекі-түсіндірмелерден теңсіздіктерге көшу арқылы маңайлар ұғымын енгізу;

4. Маңайлар арқылы тізбектің шегіне ұмтылуының барлық алты жағдайын оқушылардың

өздерін тікелей қатыстыру арқылы тұжырымдау;

5. Функцияның шексіздіктегі шегін функцияны зерттеуде, яғни горизонталь асимптотасын

табуда қолданысын талдап, мысалдар арқылы көрнекі түрде талқылау;

6. Аргумент белгілі бір шекке ұмтылғанда функцияның шексіздікке ұмтылуын оны

зерттеуде(вертикаль асимптота табу арқылы) қолдану;

7. Алдыңғы пункттер бойынша оқушылардың аргументтің маңайлары туралы ұғымдарын

қалыптастыра отырып, функцияның шексіздіктегі шегінің және нүктенің маңайында функцияның

мәндерінің шексіз өсуі мен кемуінің анықтамасын тұжырымдау;

8. Соңында функцияның осы аталған шекке ұмтылу жағдайларының бәрін қолданып, оны

зерттеп, графигінің эскизін салуға үйрету.

27.ІХ-Х сыныптарда функцияның үзіліссіздігін оқыту .

Берілген бір аралықа f(х) функциясын қарастырайық, х₀- осы аралықтан алынған нүкте. Бұл нүктеде f(х) функциясы анықталған, яғни f(х₀) – нақты сан.

Анықтама. Егер болса, онда f(х) функциясы берілген аралықтан алынған х₀ нүктесінде үздіксіз деп атайды.

Айталық х-(а,в) интервалының кез келген нүктесі болсын онда айырманы тәуелсіз айнымалы х-тің х₀ нүктесіндегі өсімшесі дейді. Бұдан .

Мына айырманы тәуелсіз айнымалы х-тің өсімшесіне сәйкес функцияның өсімшесі дейді. Енді (4.13) функцияның үздіксіздігін былайша жазамыз: .

Осыдан

Анықтама. Егер функциясы (а,в) аралығының әрбір нүктесінде үздіксіз болса, онда функциясы (а,в) аралығында үздіксіз деп аталады.

Анықтама. Егер , функциялары (а,в) аралығындағы х₀- ші нүктесінде үздіксіз болса, онда олардың қосындысы, көбейтіндісі және бөлшегі, егер ≠0, үздіксіз болады.

28-29.Туынды ұғымына келтіретін есептер. Туынды ұғымы өзара байланысты екені алдын ала екі есепті пайда болды – ол қисыққа жанама жүргізу және қозғалып бара жатқан дененің жылдамдығын табу есептері. І. Жанама туралы есеп. f функциясының графигін, яғни жазықтықта жатқан (x,f(x)) түріндегі нүктелер жиынын қарастырайық (оны y=f(x)  қисығы не жай қисық деп те атайды).  Белгілі бір (x₀,f(x₀)) нүктесінде қисыққа «тығыз орналасқан»  түзуді сызу. Әрине, ондай түзу бар болса, онда ол тек қана сол қисыққа тән қасиеттер арқылы табылады. Сондықтан, қисықта жатқан басқа (x₁,f(x₁)) нүктесін алып, сол екі нүктеден түзу өткізейік. Оның теңдеуі болады. Әрбір (x₀,f(x₀)) нүктесінен өтетін және y-тер осьіне паралель емес түзудің теңдеуі y=k(x-x₀)+f(x₀) түрінде жазылады, демек k нақты санына тәуелді болады.   Әрине, белгілі бір мағынада екі түзудің жақындығын оларды анықтайтын k сандарының жақындығы арқылы түсінуге болады. Ал, бізідң жағдайда сондай k сандары x₁-ге мынадай тәуелділікте болады. .  Сондықтан, x₁-ді x₀-ге ақырсыз жақын алған сайын, k(x₁) белгілі бір k санына ақырсыз жақындаса, онда теңдеуі болатын түзуді  бізге керекті «қисыққа тығыз  орналасқан» түзу ретінде алуға  болады.

Мұндағы k-ны тапқан жолымыз шектер тілінде былай бейнеленеді. яғни Айтқанымыздың геометриялық бейнесі 1-суретте берілген. Сонымен келесі анықтамаға келдік. Егер нүктесінде  нақты мәнді  шегі бар болса, онда  түзуі y=f(x)  қисығының нүктесіндегі  жанамасы деп аталады.   ІІ.Жылдамдық туралы есеп. Материялық нүкте түзу бойымен белгілі бір бағытта қозғалып келе жатсын. Оның түзу бойындағы белгілі бір нүктеден t мезгіліндегі  ара қашықтығы f(t)  болсын. Әуелі f(t)=a  болсын, яғни  нүкте бірқалыпты қозғалсын. Онда  кез келген   мен мезгілдері  арасында нүкте  жолын жүреді, ал  қатынасы  сол қозғалыстың жолы деп аталады  да, тұрақты болып, а санына тең болады . Егер нүктенің қозғалысы бірқалыпты болмаса, онда қатынасы  тұрақты болмай    мен мезгілдеріне  тәуелді болады. Ол    мен  мезгілдері  арасындағы материялық нүктенің  орташа жылдамдығы деп аталады. Расында, орташа жылдамдығы нүктенің  мен    мезгілдері  арасында қандай жылдамдықпен  қозғалғаны туралы ешқандай әсер  бермейді, өйткені ол бір мезгіл  жылдам, бір мезгіл жай қозғалуы  мүмкін. Орташа жылдамдық мағынасы : егер нүкте сол арада  бірқалыпты қозғалса, онда  мезгілінде жолын жүру  үшін оның жылдамдығы орташа  жылдамдыққа тең болуы тиіс.  Сонымен, айтқанымызды шек арқылы бейнелесек, мына анықтамаға келеміз. Егер нақты мәнді шегі бар болса, онда оны f тәртібі арқылы  бейнеленген қозғалыстың  нүктесіндегі  жылдамдығы деп атайды. Осы екі есеп бір-біріне өзге білім салалары – геометрия мен механикаға да жатса да,олар тек қана бір ғана математикалық амалға - түріндегі шекті табу есебіне әкеледі.   Әрине,бұл амалдың арнаулы атауы болуы керек.Ол амалдың өзін функцияны  дифференциалдау,ал оның нәтижесін,яғни шектің мәнін функцияның туындысы дейді. Сөйтіп,f функциясы І аралығында анықталсын.Егер үшін  нақты мәнді шегі бар олса,онда  f функциясын нүктесінде дифференциалданады , ал шектің мәнін f функциясының нүктесіндегі туындысы дейді де, f’(x) символымен белгілейді.