
- •1.Основные этапы статистического наблюдения. Формы, виды и способы статистического наблюдения.
- •2.Методолгические и организационные вопросы статистического наблюдения. Понятия выборочного наблюдения.
- •3. Отбор единиц в выборочную совокупность
- •4.Понятие статистической сводки и группировки. Виды группировок.
- •5.Образование групп и интервалов группировки. Вторичная группировка.
- •6.Ряды распределения
- •7.Графическое изображение рядов распределения. Виды и способы графических изображений.
- •8.Статистические таблицы, правила построения.
- •9.Абсотютные и относительные величины.
- •10.Виды и взаимосвязи относительных величин.
- •11. Относительные величины динамики, планового задания, выполнения плана, структуры, сравнения и интенсивности.
- •12.Сущность и значение средней величины.
- •13.Качественная однородность совокупности, как основное условие использования средней величины.
- •14.Виды средних и методы их расчёта.
- •15.Основные свойства средней арифметической.
- •16.Структурные средние- мода и медиана.
- •17.Понятие вариации. Показатели вариации.
- •18. Секционная диаграмма.
- •19. Относительные показатели вариации.
- •20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
- •21.Дисперсия альтернативного (качественного) признака.
- •22. Понятие о выборочном исследовании.
- •23. Отбор единиц в выборочную совокупность. Ошибка выборки.
- •24.Малая выборка. Оптимальная численность выборки.
- •25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
- •26.Корреляция и регрессия, частная корреляция…..
- •27.Метод наименьших квадратов. (мнк)
- •28.Матричная форма записи мнк
- •29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
- •30. Мультиколлинеарность.
- •31. Оценка адекватности модели.
- •32.Интерпретация моделей регрессии.
- •33. Прогнозирование по регрессионным моделям
- •34.Нелинейные модели и представление их в матричном виде.
- •35.Понятие статистических рядов динамики.
- •36.Сопоставимость рядов динамики
- •37.Базисный и цепной абсолютный прирост
- •38.Темп роста и прироста.
- •39.Средние показатели в рядах динамики.
- •40.Укрупнение интервалов
- •41.Сглаживание скользящей средней
- •42.Выравнивание с помощью мнк
- •43.Изучение сезонных явлений
- •44.Основы прогнозирования рядов динамики.
- •45.Понятие индекса
- •46.Классификация индексов
- •47.Взаимосвязь индексов
- •48.Индексы переменного состава, постоянного состава и структурных сдвигов.
25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
Конечной целью выборочного наблюдения явл. характеристика генеральной совокупности на основе выборочных результатов. Выборочные средние и относительные величины распространяют на генеральную совокупность с учётом предела их возможной ошибки. В каждой конкретной выборке расхождение между выборочной средней и генеральной может быть меньше средней ошибки выборки или равно ей, или больше её.
26.Корреляция и регрессия, частная корреляция…..
Корреляция
– это статистическая зависимость,
определяющая тесноту связи, между двумя
случайными величинами.Регрессионный
анализ,
определяет аналитическое выражение
связи между зависимой
переменной
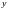 и
независимой
переменной
и
независимой
переменной
 или
независимыми
переменными
или
независимыми
переменными
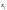 .
.
27.Метод наименьших квадратов. (мнк)
Метод
наименьших квадратов предполагает
следующие предпосылки:
1)Математическое ожидание случайных
ошибок имеет среднею равную нулю
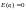 и
ошибки нормально распределены.
и
ошибки нормально распределены.
Для
проверки этого условия можно построить
гистограмму распределения ошибок
 – ось абсцисс, а ось ординат частоты
– ось абсцисс, а ось ординат частоты
 и по гистограмме можно визуально
установить близко ли распределение
ошибок к симметричному с центром равным
нулю. 2)Дисперсия случайного отклонения
постоянна
и по гистограмме можно визуально
установить близко ли распределение
ошибок к симметричному с центром равным
нулю. 2)Дисперсия случайного отклонения
постоянна
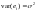 для
любого заданного значения
для
любого заданного значения
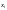 ,
следовательно, постоянна и дисперсия
зависимой переменной
,
следовательно, постоянна и дисперсия
зависимой переменной
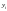 и называется гомоскедастичностью.
Когда нет постоянства дисперсии ошибок,
то такое явление называется
гетероскедастичностью.
Последствия этого следующие: оценки
параметров не будут иметь наименьшую
дисперсию по сравнению с другими
оценками, стандартная ошибка будет
смещена и выводы, полученные по
и называется гомоскедастичностью.
Когда нет постоянства дисперсии ошибок,
то такое явление называется
гетероскедастичностью.
Последствия этого следующие: оценки
параметров не будут иметь наименьшую
дисперсию по сравнению с другими
оценками, стандартная ошибка будет
смещена и выводы, полученные по
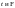 критериям,
будут неверны.
критериям,
будут неверны.
28.Матричная форма записи мнк
Матричная запись МНК. Введем обозначения:
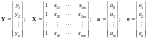
где
 – вектор наблюдений зависимых переменных;
– вектор наблюдений зависимых переменных;
 – матрица наблюдений независимых
переменных;
– матрица наблюдений независимых
переменных;
 – количество наблюдений;
– количество наблюдений;
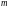 – количество независимых переменных.
– количество независимых переменных.
Модель регрессии
в матричной форме можно записать так
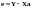 .
Для определения
.
Для определения
 минимизируем
сумму квадратов отклонений вектора
минимизируем
сумму квадратов отклонений вектора
 от
линии регрессии.
от
линии регрессии.
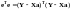
29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
Коэффициент
регрессии может быть представлен
следующим образом:
 .
.
Коэффициент
регрессии
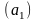 показывает меру влияния изменения
объясняющей переменной х на зависимую
переменную у. Модель регрессии в
матричной форме можно записать так
показывает меру влияния изменения
объясняющей переменной х на зависимую
переменную у. Модель регрессии в
матричной форме можно записать так
 .
Оценка
параметров регрессии по матрице парных
коэффициентов корреляции.
Результаты корреляционного анализа
можно использовать для построения
регрессионной модели. Коэффициенты
корреляции представляются в виде
вектора столбца
.
Оценка
параметров регрессии по матрице парных
коэффициентов корреляции.
Результаты корреляционного анализа
можно использовать для построения
регрессионной модели. Коэффициенты
корреляции представляются в виде
вектора столбца
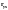 зависимой и независимых переменных и
матрицы
зависимой и независимых переменных и
матрицы
 независимых
переменных.
независимых
переменных.
 По
этим данным находятся вектор
По
этим данным находятся вектор
 стандартизованных коэффициентов
регрессии
стандартизованных коэффициентов
регрессии
 .
.
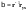
Оценка
влияния независимых переменных на
зависимую переменную затруднена, если
независимые переменные имеют различные
единицы измерения. В этом случае
используют стандартизованные
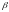 коэффициенты.
коэффициенты.
