
- •1.Основные этапы статистического наблюдения. Формы, виды и способы статистического наблюдения.
- •2.Методолгические и организационные вопросы статистического наблюдения. Понятия выборочного наблюдения.
- •3. Отбор единиц в выборочную совокупность
- •4.Понятие статистической сводки и группировки. Виды группировок.
- •5.Образование групп и интервалов группировки. Вторичная группировка.
- •6.Ряды распределения
- •7.Графическое изображение рядов распределения. Виды и способы графических изображений.
- •8.Статистические таблицы, правила построения.
- •9.Абсотютные и относительные величины.
- •10.Виды и взаимосвязи относительных величин.
- •11. Относительные величины динамики, планового задания, выполнения плана, структуры, сравнения и интенсивности.
- •12.Сущность и значение средней величины.
- •13.Качественная однородность совокупности, как основное условие использования средней величины.
- •14.Виды средних и методы их расчёта.
- •15.Основные свойства средней арифметической.
- •16.Структурные средние- мода и медиана.
- •17.Понятие вариации. Показатели вариации.
- •18. Секционная диаграмма.
- •19. Относительные показатели вариации.
- •20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
- •21.Дисперсия альтернативного (качественного) признака.
- •22. Понятие о выборочном исследовании.
- •23. Отбор единиц в выборочную совокупность. Ошибка выборки.
- •24.Малая выборка. Оптимальная численность выборки.
- •25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
- •26.Корреляция и регрессия, частная корреляция…..
- •27.Метод наименьших квадратов. (мнк)
- •28.Матричная форма записи мнк
- •29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
- •30. Мультиколлинеарность.
- •31. Оценка адекватности модели.
- •32.Интерпретация моделей регрессии.
- •33. Прогнозирование по регрессионным моделям
- •34.Нелинейные модели и представление их в матричном виде.
- •35.Понятие статистических рядов динамики.
- •36.Сопоставимость рядов динамики
- •37.Базисный и цепной абсолютный прирост
- •38.Темп роста и прироста.
- •39.Средние показатели в рядах динамики.
- •40.Укрупнение интервалов
- •41.Сглаживание скользящей средней
- •42.Выравнивание с помощью мнк
- •43.Изучение сезонных явлений
- •44.Основы прогнозирования рядов динамики.
- •45.Понятие индекса
- •46.Классификация индексов
- •47.Взаимосвязь индексов
- •48.Индексы переменного состава, постоянного состава и структурных сдвигов.
17.Понятие вариации. Показатели вариации.
Вариация- изменение значений признака внутри совокупности. Показатели вариации: рамках вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Рамках вариации- разность между максимальным и минимальным значениями признака в изучаемой совокупности. среднее линейное отклонение- средняя величина из отклонений индивидуальных значений признака от средней арифметической. Дисперсия признака- средний квадрат отклонений индивидуальных значений признака от средней величины. среднее квадратическое отклонение-корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины коэффициент вариации-отношение среднего квадратического отклонения к средней арифметической.
18. Секционная диаграмма.
Секционная
диаграмма представляет собой связь
между размахом вариации ( ), интерквартильным разбросом, определяемым
как разность между верхним (
), интерквартильным разбросом, определяемым
как разность между верхним ( )
и нижним (
)
и нижним ( )
квартилем и медианой, что позволяет
графически представить распределение
изучаемой совокупности.
)
квартилем и медианой, что позволяет
графически представить распределение
изучаемой совокупности.


Выстраивая рядом различные секционные диаграммы можно сразу получить зрительное представление о соотношении между центральными тенденциями и степенью разброса. Квартили представляют собой значение признака, делящие ранжированную совокупность на четыре равные части. Нижний квартиль отделяет 25 % совокупности с наименьшими значениями признака, т. е. 25 % единиц совокупности будут меньше по величине расчетного значения. Верхний квартиль отделяет 25 % совокупности с наибольшими значениями признака , т. е. 25 % единиц совокупности будут превышать значение. Таким образом, на интерквартильный разброс приходится 50 % изучаемой совокупности. Средний квартиль является медианой. Рассмотренные показатели могут быть рассчитаны как для интервального, так и для дискретного вариационных рядов.
19. Относительные показатели вариации.
При
сравнении колеблемости различных
признаков в одной и той же совокупности
или же при сравнении колеблемости
одного и того же признака в нескольких
совокупностях с различной величиной
средней арифметической используются
относительные показатели вариации.
Они вычисляются как соотношение
абсолютных показателей вариации к
средней арифметической (или медиане)
и чаще всего выражаются в процентах.
Формулы расчёта относительных
показателей: коэффициент осцилляции
 ,
относительное линейное отклонение
,
относительное линейное отклонение
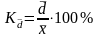 ,
коэффициент вариации
,
коэффициент вариации
 ,
относительный показатель квартильной
вариации
,
относительный показатель квартильной
вариации
 .
Совокупность считается однородной,
если коэффициент вариации не превышает
33%.
.
Совокупность считается однородной,
если коэффициент вариации не превышает
33%.
20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
Сущ. 3 вида дисперсии: 1.Общая дисперсия 2.межгрупповая- характеризует вариацию результативного признака под влиянием 1 признака фактора, положенную в основу группировки. 3.внутригрупповая- отражает случайную вариацию, происходит под влиянием неучтённых факторов. Коэффициент детерминации- это отношение характеризует, которая доля вариации признаков характеризуется под влиянием факторного признака.
