
- •1.Основные этапы статистического наблюдения. Формы, виды и способы статистического наблюдения.
- •2.Методолгические и организационные вопросы статистического наблюдения. Понятия выборочного наблюдения.
- •3. Отбор единиц в выборочную совокупность
- •4.Понятие статистической сводки и группировки. Виды группировок.
- •5.Образование групп и интервалов группировки. Вторичная группировка.
- •6.Ряды распределения
- •7.Графическое изображение рядов распределения. Виды и способы графических изображений.
- •8.Статистические таблицы, правила построения.
- •9.Абсотютные и относительные величины.
- •10.Виды и взаимосвязи относительных величин.
- •11. Относительные величины динамики, планового задания, выполнения плана, структуры, сравнения и интенсивности.
- •12.Сущность и значение средней величины.
- •13.Качественная однородность совокупности, как основное условие использования средней величины.
- •14.Виды средних и методы их расчёта.
- •15.Основные свойства средней арифметической.
- •16.Структурные средние- мода и медиана.
- •17.Понятие вариации. Показатели вариации.
- •18. Секционная диаграмма.
- •19. Относительные показатели вариации.
- •20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
- •21.Дисперсия альтернативного (качественного) признака.
- •22. Понятие о выборочном исследовании.
- •23. Отбор единиц в выборочную совокупность. Ошибка выборки.
- •24.Малая выборка. Оптимальная численность выборки.
- •25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
- •26.Корреляция и регрессия, частная корреляция…..
- •27.Метод наименьших квадратов. (мнк)
- •28.Матричная форма записи мнк
- •29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
- •30. Мультиколлинеарность.
- •31. Оценка адекватности модели.
- •32.Интерпретация моделей регрессии.
- •33. Прогнозирование по регрессионным моделям
- •34.Нелинейные модели и представление их в матричном виде.
- •35.Понятие статистических рядов динамики.
- •36.Сопоставимость рядов динамики
- •37.Базисный и цепной абсолютный прирост
- •38.Темп роста и прироста.
- •39.Средние показатели в рядах динамики.
- •40.Укрупнение интервалов
- •41.Сглаживание скользящей средней
- •42.Выравнивание с помощью мнк
- •43.Изучение сезонных явлений
- •44.Основы прогнозирования рядов динамики.
- •45.Понятие индекса
- •46.Классификация индексов
- •47.Взаимосвязь индексов
- •48.Индексы переменного состава, постоянного состава и структурных сдвигов.
14.Виды средних и методы их расчёта.
Средние,
используемые в статистике, относятся
к двум классам: степенные средние и
структурные средние. К степенным средним
величинам относятся: 1)Средняя
арифметическая величина – такое среднее
значение признака, при вычислении
которого общий объем признака в
совокупности сохраняется неизменным.
Средняя арифметическая величина
рассчитывается по формуле:
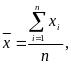 где xi
– индивидуальное значение признака
каждой единицы совокупности; n
– число единиц совокупности. 2) Взвешенная
арифметическая средняя. Рассчитывается
в случае, если совокупность велика и
исходная информация представляет собой
ряд распределения или группировку.
Взвешенная арифметическая средняя
рассчитывается по формуле:
где xi
– индивидуальное значение признака
каждой единицы совокупности; n
– число единиц совокупности. 2) Взвешенная
арифметическая средняя. Рассчитывается
в случае, если совокупность велика и
исходная информация представляет собой
ряд распределения или группировку.
Взвешенная арифметическая средняя
рассчитывается по формуле:
 где fi
– частота повторения индивидуального
значения признака (его вес); n
– число групп. 3) Средняя квадратическая
величина. Если при замене индивидуальных
величин признака на среднюю величину
необходимо сохранить неизменной сумму
квадратов исходных величин, то средняя
будет являться квадратической средней
величиной (
где fi
– частота повторения индивидуального
значения признака (его вес); n
– число групп. 3) Средняя квадратическая
величина. Если при замене индивидуальных
величин признака на среднюю величину
необходимо сохранить неизменной сумму
квадратов исходных величин, то средняя
будет являться квадратической средней
величиной ( ).
Ее формула такова:
).
Ее формула такова:
 4)Средняя геометрическая величина. Если
при замене индивидуальных величин
признака на среднюю величину необходимо
сохранить неизменным произведение
индивидуальных величин, то следует
применить геометрическую среднюю
величину. Которая рассчитывается по
формуле:
4)Средняя геометрическая величина. Если
при замене индивидуальных величин
признака на среднюю величину необходимо
сохранить неизменным произведение
индивидуальных величин, то следует
применить геометрическую среднюю
величину. Которая рассчитывается по
формуле:
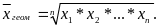 5) Средняя гармоническая величина. Если
по условиям задачи необходимо, чтобы
неизменной оставалась при осреднении
сумма величин, обратных индивидуальным
значениям признака, то средняя величина
является гармонической средней. Формула
ее расчета следующая:
5) Средняя гармоническая величина. Если
по условиям задачи необходимо, чтобы
неизменной оставалась при осреднении
сумма величин, обратных индивидуальным
значениям признака, то средняя величина
является гармонической средней. Формула
ее расчета следующая:
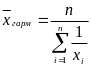 .
К структурным средним относятся:
1)Медиана. В статистике медианой называют
признак, делящий численность вариационного
ряда по сумме накопленных частот на
две равные части. Медиана лежит в
середине ранжированного ряда и делит
его пополам. Расчет медианы по
несгруппированным данным производится
следующим образом: а) индивидуальные
значения признака располагаются в
возрастающем порядке; б) определяется
порядковый номер медианы по формуле:
.
К структурным средним относятся:
1)Медиана. В статистике медианой называют
признак, делящий численность вариационного
ряда по сумме накопленных частот на
две равные части. Медиана лежит в
середине ранжированного ряда и делит
его пополам. Расчет медианы по
несгруппированным данным производится
следующим образом: а) индивидуальные
значения признака располагаются в
возрастающем порядке; б) определяется
порядковый номер медианы по формуле:
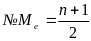
2)Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. Определить величину моды в первичном ряду в точном соответствии с данным правилом возможно только при достаточно большом количестве наблюдений и при условии, что одно из индивидуальных значений изучаемого признака у отдельных единиц совокупности повторяется значительно чаще, чем все другие значения.
15.Основные свойства средней арифметической.
Средняя арифметическая величина – такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Средняя арифметическая величина рассчитывается по формуле: где xi – индивидуальное значение признака каждой единицы совокупности; n – число единиц совокупности.
16.Структурные средние- мода и медиана.
К структурным средним относятся:1) Медиана. В статистике медианой называют признак, делящий численность вариационного ряда по сумме накопленных частот на две равные части. Медиана лежит в середине ранжированного ряда и делит его пополам. Расчет медианы по несгруппированным данным производится следующим образом: а) индивидуальные значения признака располагаются в возрастающем порядке; б) определяется порядковый номер медианы по формуле:
2)Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. Определить величину моды в первичном ряду в точном соответствии с данным правилом возможно только при достаточно большом количестве наблюдений и при условии, что одно из индивидуальных значений изучаемого признака у отдельных единиц совокупности повторяется значительно чаще, чем все другие значения.
