
- •1.Основные этапы статистического наблюдения. Формы, виды и способы статистического наблюдения.
- •2.Методолгические и организационные вопросы статистического наблюдения. Понятия выборочного наблюдения.
- •3. Отбор единиц в выборочную совокупность
- •4.Понятие статистической сводки и группировки. Виды группировок.
- •5.Образование групп и интервалов группировки. Вторичная группировка.
- •6.Ряды распределения
- •7.Графическое изображение рядов распределения. Виды и способы графических изображений.
- •8.Статистические таблицы, правила построения.
- •9.Абсотютные и относительные величины.
- •10.Виды и взаимосвязи относительных величин.
- •11. Относительные величины динамики, планового задания, выполнения плана, структуры, сравнения и интенсивности.
- •12.Сущность и значение средней величины.
- •13.Качественная однородность совокупности, как основное условие использования средней величины.
- •14.Виды средних и методы их расчёта.
- •15.Основные свойства средней арифметической.
- •16.Структурные средние- мода и медиана.
- •17.Понятие вариации. Показатели вариации.
- •18. Секционная диаграмма.
- •19. Относительные показатели вариации.
- •20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
- •21.Дисперсия альтернативного (качественного) признака.
- •22. Понятие о выборочном исследовании.
- •23. Отбор единиц в выборочную совокупность. Ошибка выборки.
- •24.Малая выборка. Оптимальная численность выборки.
- •25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
- •26.Корреляция и регрессия, частная корреляция…..
- •27.Метод наименьших квадратов. (мнк)
- •28.Матричная форма записи мнк
- •29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
- •30. Мультиколлинеарность.
- •31. Оценка адекватности модели.
- •32.Интерпретация моделей регрессии.
- •33. Прогнозирование по регрессионным моделям
- •34.Нелинейные модели и представление их в матричном виде.
- •35.Понятие статистических рядов динамики.
- •36.Сопоставимость рядов динамики
- •37.Базисный и цепной абсолютный прирост
- •38.Темп роста и прироста.
- •39.Средние показатели в рядах динамики.
- •40.Укрупнение интервалов
- •41.Сглаживание скользящей средней
- •42.Выравнивание с помощью мнк
- •43.Изучение сезонных явлений
- •44.Основы прогнозирования рядов динамики.
- •45.Понятие индекса
- •46.Классификация индексов
- •47.Взаимосвязь индексов
- •48.Индексы переменного состава, постоянного состава и структурных сдвигов.
42.Выравнивание с помощью мнк
Для
нахождения неизвестных коэффициентов
методом наименьших квадратов (МНК)
можно составить систему нормальных
уравнений для рассмотренных функций
и решить их, определив неизвестные
коэффициенты ,
,
 и
и
 .
Рассмотрим пример составления системы
нормальных уравнений для гиперболической
функции. МНК минимизирует сумму квадратов
отклонений (
.
Рассмотрим пример составления системы
нормальных уравнений для гиперболической
функции. МНК минимизирует сумму квадратов
отклонений (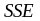 )
наблюдаемых значений от теоретических.
Символьно это можно записать так.
)
наблюдаемых значений от теоретических.
Символьно это можно записать так.
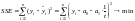 где
где
 – наблюдаемые значения временного
ряда;
– наблюдаемые значения временного
ряда;
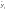 – теоретические значения временного
ряда;
– временные отсчеты, например, годы
– теоретические значения временного
ряда;
– временные отсчеты, например, годы
 ;
– количество наблюдаемых значений
временного ряда;
;
– количество наблюдаемых значений
временного ряда;
 – неизвестные коэффициенты.
– неизвестные коэффициенты.
43.Изучение сезонных явлений
Под
сезонными
колебаниями
понимается устойчивое колебание ряда
динамики, повторяющееся через определенные
периоды времени в течение года.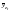 .
После этого определяем индивидуальные
индексы сезонности по формуле.
.
После этого определяем индивидуальные
индексы сезонности по формуле.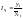 Затем находим средние значения
индивидуальных индексов сезонностей
по формуле.
Затем находим средние значения
индивидуальных индексов сезонностей
по формуле.
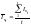 где
– количество периодов, по которым
рассчитывается индивидуальные индексы
сезонности.
Используя полученные средние значения
индексов сезонностей, очищают исходный
ряд динамики от сезонной составляющей,
получая тренд.
где
– количество периодов, по которым
рассчитывается индивидуальные индексы
сезонности.
Используя полученные средние значения
индексов сезонностей, очищают исходный
ряд динамики от сезонной составляющей,
получая тренд. Затем
определяют теоретические значения
тренда
Затем
определяют теоретические значения
тренда
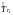 по приведенным выше функциям от времени.
Для осуществления прогноза может быть
использована следующая модель
по приведенным выше функциям от времени.
Для осуществления прогноза может быть
использована следующая модель

44.Основы прогнозирования рядов динамики.
При анализе временных рядов в экономике обычно предполагается, что наблюдения упорядочены во времени и разделены равными интервалами времени. Согласно одной из традиционных моделей экономические временные ряды содержат четыре компоненты: тренд, сезонное изменение, циклическое изменение и случайную компоненту. Эти компоненты необходимо определить и этот процесс называется декомпозицией. Эти четыре компоненты представляют в виде мультипликативной или аддитивной модели.
45.Понятие индекса
Индекс – относительная величина, характеризующая изменение уровней сложных социально-экономических показателей по времени, в пространстве или по сравнению с планом. Сложный показатель состоит из непосредственно несоизмеримых элементов. Индексные показатели вычисляются на высшей ступени статистического обобщения и опираются на результаты сводки и обработки данных статистического наблюдения. С их помощью решаются следующие задачи: - Характеристика общего изменения сложного экономического показателя и отдельных его элементов; - Измерение влияния факторов на общую динамику сложного показателя, включая характеристику влияния изменения структуры явления. Индекс является результатом сравнения двух одноимённых показателей, поэтому при их вычислении различают сравниваемый уровень, называемый текущим или отчётным, и уровень, с которым производится сравнение, называемый базисным.
46.Классификация индексов
Классификация индексов представлена на рис.
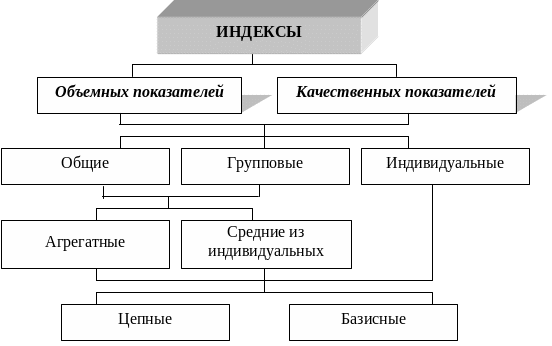
К индексам объемных показателей относятся индексы физического объема продукции, физического объема товарооборота, физического объема национального дохода и т.д. Индексы качественных показателей включают в себя индексы цен, себестоимости, производительности труда и др. Общие индексы характеризуют изменение совокупности в целом, например валовой продукции народного хозяйства в отчетном году по сравнению с предыдущим. Индивидуальные индексы дают сравнительную характеристику динамики отдельных элементов совокупности, например выпуска чугуна в двух периодах. Групповые индексы характеризуют динамику не всей совокупности, а только ее части, например индекс валовой продукции машиностроительной отрасли. Агрегатные и средние из индивидуальных показатели определяются методологией их расчета. Если база для сравнения всех уровней явления остается постоянной, получаемый индекс называют базисным, в противном случае – цепным.
