- •1.Основные этапы статистического наблюдения. Формы, виды и способы статистического наблюдения.
- •2.Методолгические и организационные вопросы статистического наблюдения. Понятия выборочного наблюдения.
- •3. Отбор единиц в выборочную совокупность
- •4.Понятие статистической сводки и группировки. Виды группировок.
- •5.Образование групп и интервалов группировки. Вторичная группировка.
- •6.Ряды распределения
- •7.Графическое изображение рядов распределения. Виды и способы графических изображений.
- •8.Статистические таблицы, правила построения.
- •9.Абсотютные и относительные величины.
- •10.Виды и взаимосвязи относительных величин.
- •11. Относительные величины динамики, планового задания, выполнения плана, структуры, сравнения и интенсивности.
- •12.Сущность и значение средней величины.
- •13.Качественная однородность совокупности, как основное условие использования средней величины.
- •14.Виды средних и методы их расчёта.
- •15.Основные свойства средней арифметической.
- •16.Структурные средние- мода и медиана.
- •17.Понятие вариации. Показатели вариации.
- •18. Секционная диаграмма.
- •19. Относительные показатели вариации.
- •20.Виды дисперсий и правило их сложения. Коэффициент детерминации.
- •21.Дисперсия альтернативного (качественного) признака.
- •22. Понятие о выборочном исследовании.
- •23. Отбор единиц в выборочную совокупность. Ошибка выборки.
- •24.Малая выборка. Оптимальная численность выборки.
- •25.Распространение выборочных результатов на генеральную совокупность. Причинно-следственные отношения и формы связи.
- •26.Корреляция и регрессия, частная корреляция…..
- •27.Метод наименьших квадратов. (мнк)
- •28.Матричная форма записи мнк
- •29. Оценка коэффициентов регрессии по матрице парных коэффициентов корреляции.
- •30. Мультиколлинеарность.
- •31. Оценка адекватности модели.
- •32.Интерпретация моделей регрессии.
- •33. Прогнозирование по регрессионным моделям
- •34.Нелинейные модели и представление их в матричном виде.
- •35.Понятие статистических рядов динамики.
- •36.Сопоставимость рядов динамики
- •37.Базисный и цепной абсолютный прирост
- •38.Темп роста и прироста.
- •39.Средние показатели в рядах динамики.
- •40.Укрупнение интервалов
- •41.Сглаживание скользящей средней
- •42.Выравнивание с помощью мнк
- •43.Изучение сезонных явлений
- •44.Основы прогнозирования рядов динамики.
- •45.Понятие индекса
- •46.Классификация индексов
- •47.Взаимосвязь индексов
- •48.Индексы переменного состава, постоянного состава и структурных сдвигов.
30. Мультиколлинеарность.
Мультиколлинеарность
(для множественной регрессии) – высокая
коррелированность матрицы парных
коэффициентов корреляции независимых
переменных. Получаемые параметры
регрессии имеют большие стандартные
ошибки и проверка их значимости по
 -
критерию Стьюдента не имеет смысла.
Оценки параметров регрессии очень
чувствительны к изменению объема
выборки и к результатам наблюдений.
-
критерию Стьюдента не имеет смысла.
Оценки параметров регрессии очень
чувствительны к изменению объема
выборки и к результатам наблюдений.
31. Оценка адекватности модели.
Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Анализ качества эмпирического уравнения парной и множественной линейной регрессии начинают с построения эмпирического уравнения регрессии, которое является начальным этапом эконометрического анализа. Первое же, построенное по выборке, уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:
проверка статистической значимости коэффициентов уравнения регрессии
проверка общего качества уравнения регрессии
проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК)
Проверка адекватности
всей модели, т.е. коэффициента детерминации
 осуществляется с помощью критерия
Фишера.
осуществляется с помощью критерия
Фишера.
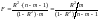 где
где
 – дисперсия, отнесенная к регрессии
(объясненная дисперсия);
– дисперсия, отнесенная к регрессии
(объясненная дисперсия);
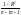 – остаточная регрессия.
– остаточная регрессия.
32.Интерпретация моделей регрессии.
Интерпретация модели. Если построенная модель прошла все проверки, то такую модель можно использовать для анализа и прогноза.
33. Прогнозирование по регрессионным моделям
Прогнозирование – это определение ориентировочных размеров явлений в будущем.
Полученную регрессионную модель можно использовать для прогнозирования по тем значениям независимых переменных, которые не наблюдались в представленной выборке.
34.Нелинейные модели и представление их в матричном виде.
Нелинейные модели и представление их в матричном виде. Различают три вида нелинейных моделей:
1) Нелинейные модели, которые могут быть преобразованы к линейной форме, например.
-
показательная
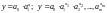 ;
- степенная
;
- степенная
 ;
- гиперболическая
;
- гиперболическая
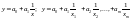 ;
- параболическая
;
- параболическая
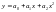 .
Ясно, что такие нелинейные функции
можно свести к линейным уравнениям,
взяв логарифм от двух частей уравнений
или заменой переменной. Например, для
степенной функции
.
Ясно, что такие нелинейные функции
можно свести к линейным уравнениям,
взяв логарифм от двух частей уравнений
или заменой переменной. Например, для
степенной функции
 ,
или для гиперболической, введя обозначения
,
или для гиперболической, введя обозначения
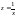 ,
получим
,
получим
 .
2)Нелинейные модели, которые линейные
по неизвестным параметрам.
.
2)Нелинейные модели, которые линейные
по неизвестным параметрам.
 ;
;
 ;
;
 .
3) Нелинейные модели, которые не могут
быть преобразованы к линейной форме,
например.
.
3) Нелинейные модели, которые не могут
быть преобразованы к линейной форме,
например.

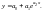 В последнем примере для того, чтобы
оценить параметры
В последнем примере для того, чтобы
оценить параметры
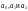 ,
требуется использование нелинейного
МНК, такие возможности предоставляют
многие статистические программы. Для
первых двух типов нелинейных моделей
запись их в матричном виде и оценка
неизвестных параметров может быть
осуществлена следующим образом.
Для полинома второй степени
,
требуется использование нелинейного
МНК, такие возможности предоставляют
многие статистические программы. Для
первых двух типов нелинейных моделей
запись их в матричном виде и оценка
неизвестных параметров может быть
осуществлена следующим образом.
Для полинома второй степени
 .
.
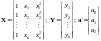 Для экспоненциальной
кривой
Для экспоненциальной
кривой
 .
.
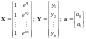 Для функции вида
Для функции вида
 .
.
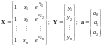 Для функции вида
Для функции вида
 .
.