Задание 3.

s_n+b = s_n+b-2 + s_n

s_n+6 = s_n+4 + s_n

3.1. Нарисовать электронную схему последовательности.

n+6

n+4

n

2. Найти характеристический многочлен последовательности и разложить его на множители.

S_n+6 = S_n+4 + S_n

S_n+6 – S_n-4 – S_n = 0

В таком случае характеристическое уравнение будет иметь вид:

х⁶ – х⁴ – 1 = 0

Вероятнее всего (учитывая последующие задания и использование регистров сдвига для моделирования последовательности), все вычисления проводятся не в поле действительных (или комплексных) чисел, а в поле GF(2^k+1), то есть в поле GF(2⁷). В задании явно не указано, в каком поле проводить вычисления. Данный многочлен имеет в поле действительных чисел 2 корня, и 4 корня в поле комплексных чисел. Решение последующих заданий (а именно 3.4, 3.5, 3.6) возможно только в поле GF(2⁷), поэтому дальнейшее решение будет представлено для этого поля.

В таком случае характеристическое уравнение примет вид:

х⁶ + х⁴ + 1 = 0

И разложится на множители до неприводимых элементов:

(х³ + х² + 1)² = 0

2. Найти явную формулу для n-го члена рекуррентной последовательности.

Явная формула для n-го члена рекуррентной последовательности:

S_n = β₁ + β₂ + β₃ + β₄ + β₅ + β₆

Где α₁, α₂, α₃, α₄, α₅, α₆ – корни характеристического уравнения. В поле GF(2⁷) характеристическое уравнение решений не имеет, следовательно невозможно записать явное уравнение n-го члена через формулу. Для поля комплексных чисел, где могут быть найдены корни уравнения х⁶ - х⁴ - 1 = 0, можно записать явную формулу n-го члена. Корни уравнения будут:

α₁ = 1,211

α₂ = -1,211

α₃ = 0,74 + 0,53i

α₄ = 0,74 + 0,53i

α₅ = 0,74 – 0,53i

α₆ = 0,74 – 0,53i

Среди корней присутствуют кратные, значит явная формула n-го члена примет общий вид:

S_n =

β₁, β₂, β₃, β₄, β₅, β₆ находятся при решении системы уравнений:

Решить эту систему не представляется возможным, так как не известны первые k членов последовательности (S₀, S₁, S₂, S₃, S₄, S₅) – вектор инициализации. Явная формула n-го члена последовательности в таком случае будет иметь вид:

S_n =

2. Найти период последовательности «в лоб»

0000001 - шаг 1

0000010 - шаг 2

0000100 - шаг 3

0001001 - шаг 4

0010010 - шаг 5

0100100 - шаг 6

1001001 - шаг 7

0010011 - шаг 8

0100110 - шаг 9

1001101 - шаг 10

0011010 - шаг 11

0110100 - шаг 12

1101001 - шаг 13

1010011 - шаг 14

0100111 - шаг 15

1001111 - шаг 16

0011110 - шаг 17

0111101 - шаг 18

1111011 - шаг 19

1110111 - шаг 20

1101110 - шаг 21

1011100 - шаг 22

0111000 - шаг 23

1110000 - шаг 24

1100001 - шаг 25

1000011 - шаг 26

0000111 - шаг 27

0001111 - шаг 28

0011111 - шаг 29

0111111 - шаг 30

1111111 - шаг 31

1111110 - шаг 32

1111100 - шаг 33

1111000 - шаг 34

1110001 - шаг 35

1100011 - шаг 36

1000111 - шаг 37

0001110 - шаг 38

0011101 - шаг 39

0111011 - шаг 40

1110110 - шаг 41

1101100 - шаг 42

1011000 - шаг 43

0110001 - шаг 44

1100010 - шаг 45

1000101 - шаг 46

0001010 - шаг 47

0010100 - шаг 48

0101001 - шаг 49

1010010 - шаг 50

0100101 - шаг 51

1001011 - шаг 52

0010111 - шаг 53

0101111 - шаг 54

1011111 - шаг 55

0111110 - шаг 56

1111101 - шаг 57

1111010 - шаг 58

1110101 - шаг 59

1101010 - шаг 60

1010101 - шаг 61

0101010 - шаг 62

1010100 - шаг 63

0101000 - шаг 64

1010000 - шаг 65

0100001 - шаг 66

1000010 - шаг 67

0000101 - шаг 68

0001011 - шаг 69

0010110 - шаг 70

0101101 - шаг 71

1011011 - шаг 72

0110111 - шаг 73

1101111 - шаг 74

1011110 - шаг 75

0111100 - шаг 76

1111001 - шаг 77

1110011 - шаг 78

1100111 - шаг 79

1001110 - шаг 80

0011100 - шаг 81

0111001 - шаг 82

1110010 - шаг 83

1100101 - шаг 84

1001010 - шаг 85

0010101 - шаг 86

0101011 - шаг 87

1010110 - шаг 88

0101100 - шаг 89

1011001 - шаг 90

0110011 - шаг 91

1100110 - шаг 92

1001100 - шаг 93

0011000 - шаг 94

0110000 - шаг 95

1100000 - шаг 96

1000001 - шаг 97

0000011 - шаг 98

0000110 - шаг 99

0001101 - шаг 100

0011011 - шаг 101

0110110 - шаг 102

1101101 - шаг 103

1011010 - шаг 104

0110101 - шаг 105

1101011 - шаг 106

1010111 - шаг 107

0101110 - шаг 108

1011101 - шаг 109

0111010 - шаг 110

1110100 - шаг 111

1101000 - шаг 112

1010001 - шаг 113

0100011 - шаг 114

1000110 - шаг 115

0001100 - шаг 116

0011001 - шаг 117

0110010 - шаг 118

1100100 - шаг 119

1001000 - шаг 120

0010001 - шаг 121

0100010 - шаг 122

1000100 - шаг 123

0001000 - шаг 124

0010000 - шаг 125

0100000 - шаг 126

1000000 - шаг 127

0000001 - шаг 128

В теоретическом материале было указано, что наибольший период получается при векторе инициализации (0, 0, 0, 0, 0, 0, 1). Такой вектор называется импульсной функцией. При использовании данного вектора инициализации, период получается равен 127, что является наибольшим возможным периодом для данного регистра сдвига (2⁷-1).

2. Найти, в какой степени матрица последовательности станет равной единичной.

Предположим, что начальное состояние последовательности (0, 0, 0, 0, 0, 0, 1), которое соответствует максимальному периоду рекуррентной последовательности.

Матрица при данных начальных условиях будет иметь вид:

A =

Найдем степень, в которой матрица А станет равной единичной, то есть А^m = E

A² =

A³ =

A⁴ =

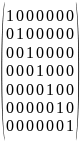
2. Найти в какой степени элемент α станет равным 1

Элемент α в нашем регистре будет иметь запись (0, 0, 0, 0, 0, 1, 0)

Элемент 1 в нашем регистре будет иметь запись (0, 0, 0, 0, 0, 0, 1)

Следовательно, надо найти на каком шаге регистр, при векторе инициации α даст 1. Учитывая, что период последовательности = 127, а элемент α следует сразу же за элементом 1, можно утверждать что α¹²⁶ = 1.