3. Проектирование активных фильтров

№ варианта	К0	Fp, КГц	q
4	1	60	10

1. Расчет активного полосового фильтра 2-го порядка для 3-х способов реализации:

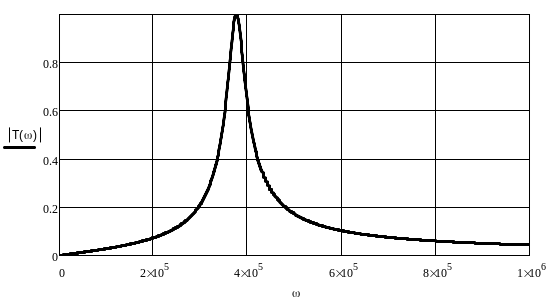
• Л1, стр. 54, рис.5.3,

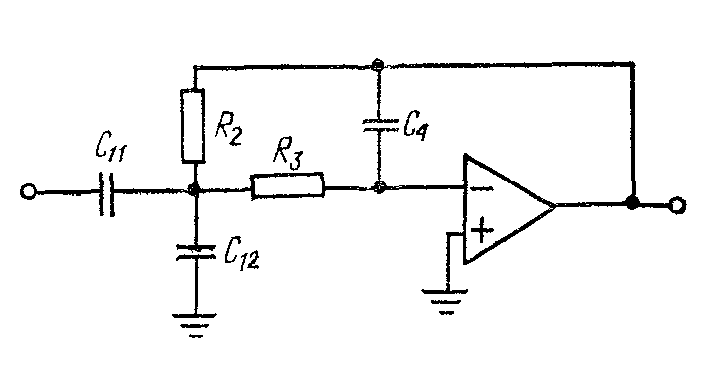
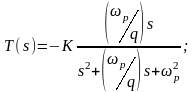
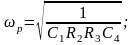
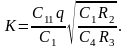
Определение параметров элементов схемы:

Емкости С₁ = С₁₁ + С₁₂ и С₄ определяются исходя из следующего соотношения:

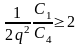
Следовательно,

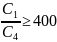
Выберем С₁ = 4 нФ, С₄ = 0,01 нФ. Тогда ,

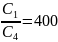
Для определения других параметров необходимо найти значение вспомогательной величины Р:

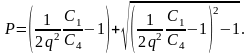
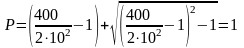
определение сопротивлений резисторов:

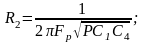
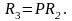
Подставляя ранее найденные величины, получим R₂= R₃ ≈13,3 КОм

Значения емкостей С₁₁ и С₁₂ определяются исходя из требуемого коэффициента передачи на резонансной частоте:

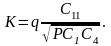
Следовательно, при К = 1:

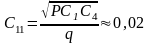нФ;

С₁₂ = С₁ – С₁₁ ≈ 3, 98 нФ.

Из формул для данного фильтра видно, что ω_р и q можно настраивать независимо друг от друга с помощью R₂ и R₃: для настройки частоты необходимо изменять значения сопротивлений резисторов так, чтобы не менялось их отношение, а для настройки q – так, чтобы не менялось их произведение. Полосу пропускания, соответственно, можно настраивать с теми же резисторами, изменяя отношение ω_р к q.

• Л1, стр. 61, рис.5.10,

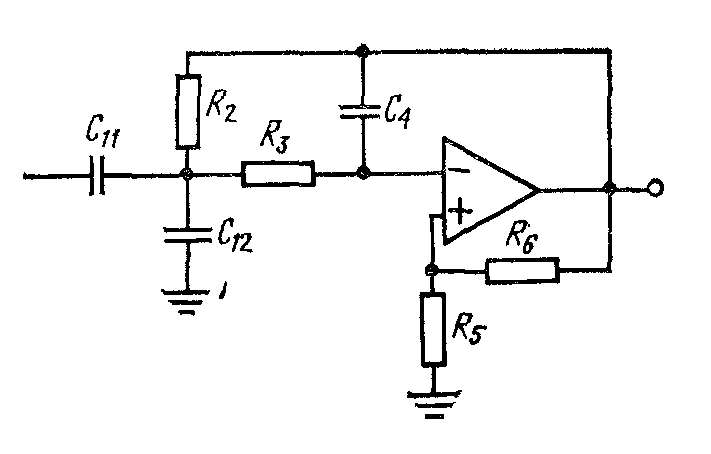
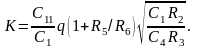
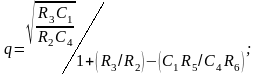
Определение параметров элементов схемы:

Пусть С₁ = С₄ = 1 нФ

Определим вспомогательную величину Р:

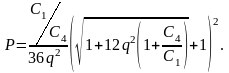
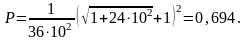
Сопротивления резисторов:

Примем R₆ = 10 КОм, тогда

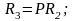
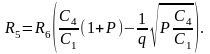
Значения сопротивлений R₂ ≈ 4,18 КОм; R₃ ≈ 2,9 КОм; R₅ ≈ 6,73 кОм.

Соотношение емкостей С₁₁ и С₁₂ определим из выражения для коэффициента передачи на резонансной частоте:

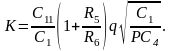
При К = 1:

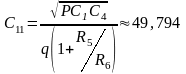пФ;

С₁₂ = С₁ – С₁₁ ≈ 950,2 пФ. Из формул для данного фильтра видно, что ω_р и q можно настраивать независимо друг от друга с помощью R₂ и R₃: для настройки частоты необходимо изменять значения сопротивлений резисторов так, чтобы не менялось их отношение, а для настройки q – так, чтобы не менялось их произведение. Полосу пропускания, соответственно, можно настраивать с теми же резисторами, изменяя отношение ω_р к q. Также q можно подстроить с помощью R₅ и R₆.

• Л1, стр. 76, рис.5.23, выходной сигнал берется с выхода, которому соответствует передаточная функция 22(в).

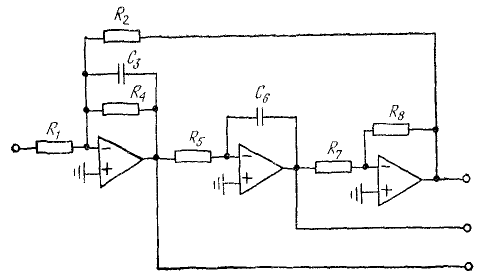
Для выхода, соответствующего полосовому фильтру:

Выражение для передаточной функции в данном случае принимает вид:

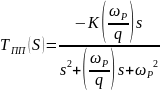
Выражение для резонансной частоты:

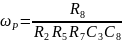
Выражение для добротности:

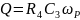
Выражение для коэффициента усиления:

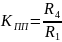
Данный фильтр является универсальным. Его эквивалентная схема представляет собой звено второго порядка, причем для получения полосового фильтра сигнал снимается с резистора.

Возьмем C=1 нФ.

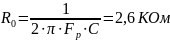
Возьмем R_d=10 КОм, тогда

R₂=R₇=R₈=R_d=10 КОм

С₃=С₆=С=1 нФ

R₅=R₀²/R_d=0,676 КОм

R₄=q*R₀=26 КОм

R₁=R₄/K=26 КОм

К_пп=К=1

К_нч1=К_нч2=R₂/R₁=0,384

Настройка ω_р осуществляется резисторами R_2,5,7,8, q настраивается аналогично + R₄.

2. Анализ для 3-х способов реализации:

• Чувствительности перечисленных параметров к разбросу элементов.

Чувствительность q

Расcчитано в среде MathCad

1-й способ реализации

С₁ – 0,48, С₄ – 0,47 R₂ – 0,12, R₃ – 0,14

2-й способ реализации

С₁ –2,5, С₄ – 4,98 R₅ – 2,86, R₆ – 5,71 R₂ – 0,88, R₃ – 1,04

3-й способ реализации

С₆, С₈ – 0,54 R₅, R₇ – 0,54

Чувствительность Δω

1-й способ реализации

С₁ – 0,91, С₄ – 0 R₂ – 0,58, R₃ – 0,33

2-й способ реализации

С₁ –2,73, С₄ – 3,64 R₂ – 0,45, R₃ – 1,36,R₅ – 4, R₆ – 3,64

3-й способ реализации

R₅ – 0,35, С₆ – 0,91

Набольшей чувствительностью к разбросу параметров элементов обладает фильтр, реализованный по второму способу. Первый и третий способы реализации фильтров обладают меньшей чувствительностью. Таким образом, можно считать их наименее чувствительными к разбросу параметров элементов.