1 8. Преломление силовых линий на границе раздела диэлектриков.

Допустим, что на границе раздела диэлектриком нет свободных зарядов. Тогда . Если , тогда и, следовательно, силовые линии ведут себя так, как показано на рисунке, т.е. силовые линии удаляются от нормали, входя в диэлектрик с большой диэлектрической проницаемостью.

19. Энергия взаимодействия дискретных зарядов.

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.  При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА. Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов (1). Энергия взаимодействия двух точечных зарядов q₁ и q₂, находящихся на расстоянии r₁₂, численно равна работе по перемещению заряда q₁ в поле неподвижного заряда q₂ из точки с потенциалом  в точку с потенциалом : Будем считать аддитивную постоянную W₀, равной нулю. В этом случае W может быть и отрицательной величиной, если q₁ и q₂ - заряды противоположного знака. Аналогично можно рассчитать энергию двух зарядов, рассмотрев перемещение заряда q₂ в поле неподвижного заряда q₁ из точки с потенциалом  в точку с потенциалом (2). Удобно записать энергию взаимодействия двух зарядов в симметричной форме (3).

Д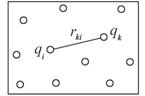 ля системы из n точечных зарядов (рис 1.) в силу принципа суперпозиции для потенциала, в точке нахождения k-го заряда, можно записать: Здесь φ_k,i - потенциал i-го заряда в точке расположения k-го заряда. В сумме исключен потенциал φ_k,k, т.е. не учитывается воздействие заряда самого на себя, равное для точечного заряда бесконечности.

Тогда взаимная энергия системы n зарядов равна: (4)

20. Плотность энергии электрического поля.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую. При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:  Электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость   Поэтому где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина  является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии. Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности w_е по всему объему, в котором создано электрическое поле.