15. Электрическое смещение. Поле плоского конденсатора.

В неоднородной диэлектрической среде   имеет различные значения, изменяясь на границах диэлектриков скачкообразно (претерпевая разрыв). Благодаря различной поляризуемости разнородных диэлектриков напряженности поля в них будут различными. Поэтому различно и число силовых линий в каждом диэлектрике. Часть линий, исходящих из зарядов, окруженных замкнутой поверхностью, будет заканчиваться на границе раздела диэлектриков и не пронижет данную поверхность. Это затруднение можно устранить, введя в рассмотрение новую физическую характеристику поля – вектор электрического смещения . Вектор   направлен в ту же сторону, что и   . В отличие от напряженности поля   вектор   имеет постоянное значение во всех диэлектриках. Поэтому электрическое поле в неоднородной диэлектрической среде удобнее характеризовать не напряженностью  , а смещением  . С этой целью вводится понятие линий вектора   и потока смещения, аналогично понятию силовых линий и потока напряженности . Используя теорему Гаусса и с учетом формулы смещения получаем: Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.

Плоский конденсатор представляет собой две металлические пластины, расположенные параллельно друг другу на малом по сравнению с размерами пластин расстоянии друг от друга. При сообщении пластинам одинаковых по модулю зарядов разных знаков в пространстве между пластинами возникает практически однородное электрическое поле. Однородность поля нарушается только вблизи краев пластин (краевой эффект). Можно изменять значение поверхностной плотности заряда σ = Q / S на пластинах и величину пробного заряда q.

16. Теорема Гаусса при наличии диэлектриков.

(3)  т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.  Для вакуума D_n = ε₀E_n (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен

  Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как    где ∑Q_i и ∑Q_sv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения. 

17. Граничные условия для нормальной и тангенциальной компонент электрического поля.

Граничные условия для тангенциальных составляющих электрического поля.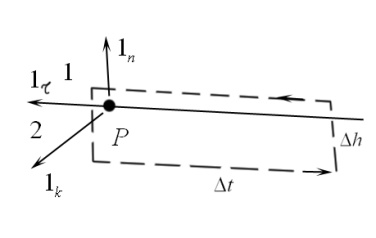

У нас есть:  + циркуляция по боковым сторонам

 

Функция  стоящая в правой части этого состава является величиной конечной для любых граничащих сред, отчего предельный переход при  дает 

откуда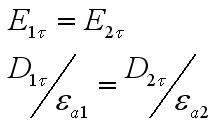   

Тем самым, на границе раздела сред тангенциальные составляющие векторов напряженности электрического поля непрерывны, тем не менее похожие составляющие векторов электрического смещения, вообще объясняясь, претерпевают разрыв. Проанализируем в отдельности граничные условия в том случае, когда средой 2 на изображении выше является безупречный металл. Как уже известно, здесь, всегда  . Если же внутри безупречного металла имелась конечная напряженность электрического поля, то это повергло бы к протеканию тут нескончаемо больших токов проводимости и, как результат, к выделению нескончаемо немалого количества тепла, что возражает физической сущности задачи. Значит с учетом выше изложенного, для идеального проводника граничное условие принимает вид  . Силовые линии электрического поля в соответствии с этим условием должны подходить по направлению нормали к поверхности безупречного металла. Соображение "безупречный металл" является абстрактным и на границе раздела с реальным металлом имеется кое-какая тангенциальная составляющая электрического поля. Все же будет показано, что она достаточно мала, так что значительно во многих задачах её можно не учитывать. 

Граничные условия для нормальных составляющих электрического поля.  Д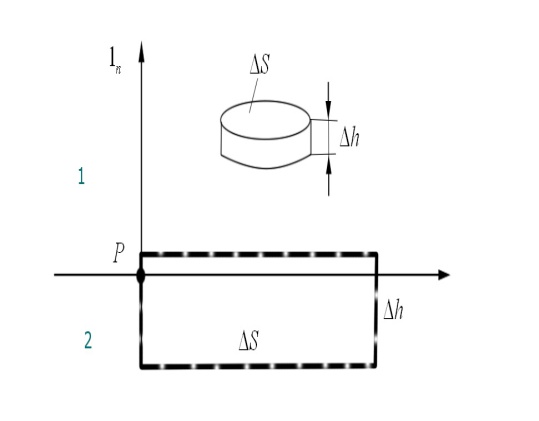 ля электрического поля имеем: . Тут возможны два случая: 1. Плотность электрических поверхностных зарядов равна нулю. Заключенный внутри малой цилиндрической области суммарный электрический заряд равен нулю. В соответствии с теоремой Гаусса  , откуда следует  и   

Следовательно, в отсутствии поверхностных электрических зарядов на границе раздела двух сред, нормальные составляющие векторов электрического смещения непрерывны, в тот момент как в общем случае нормальные составляющие напряженностей электрического поля претерпевают скачок. 2. Равномерно распределен на границе раздела поверхностный электрический заряд с плотностью  . В таком случае, явно не влияет на величину заряда стремление к нулю высоты цилиндра  , заключенного внутри области. Можно записать формулу, воспользовавшись законом Гаусса,  откуда  . Согласно изображению выражения выше следует, что нормальные составляющие векторов электрического смещения при наличии заряженной границы раздела испытывают скачок на величину плотности поверхностного заряда в исследуемой точке. Это обусловлено физически тем, что расположенный на поверхности заряд формирует собственное поле, ориентированное так, что от границы раздела по одну сторону это поле складывается с внешним полем, а по другую вычитается.