
- •2. Элементарный заряд и его инвариантность.
- •3. Закон сохранения заряда.
- •4. Дифференциальная формулировка закона Кулона.
- •5. Теорема Гаусса
- •6. Потенциальность электростатического поля.
- •7. Скалярный потенциал.
- •8. Уравнения Лапласа и Пуассона. Вычисление напряженности поля внутри и вне заряженного цилиндра.
- •9. Электростатическое поле при наличии проводников.
- •10. Емкость уединенного проводника. Конденсаторы
- •11. Дипольный момент непрерывного распределения зарядов.
- •12. Зависимость поляризованности от напряженности электрического поля. Влияние поляризации на электрическое поле.
- •13. Поле диполя
- •14. Поляризация диэлектриков. Поляризованность. Объемная и поверхностная плотности связанных зарядов.
- •15. Электрическое смещение. Поле плоского конденсатора.
- •16. Теорема Гаусса при наличии диэлектриков.
- •17. Граничные условия для нормальной и тангенциальной компонент электрического поля.
- •1 8. Преломление силовых линий на границе раздела диэлектриков.
- •19. Энергия взаимодействия дискретных зарядов.
- •20. Плотность энергии электрического поля.
- •21. Силы, действующие на точечный заряд, непрерывно распределенный заряд, диполь в электрическом поле.
- •22. Опыт Милликена.
- •23. Механизм поляризации неполярных диэлектриков.
- •24. Механизм поляризации полярных диэлектриков.
- •25. Закон Ома в интегральной и дифференциальной форме.
- •26. Работа и мощность тока
- •27. Правила Кирхгофа.
- •28. Опыт Толмена и Стюарта.
- •29. Эффект Холла.
- •30. Зависимость электропроводности от температуры, сверхпроводимость.
- •31. Понятие о зонной теории твердых тел. Энергетические зоны проводников, полупроводников и диэлектриков.
- •32. Собственная и примесная проводимость полупроводников. Доноры и акцепторы.
- •3 3. Эффект Пельтье. Эффект Томпсона. Эффект Зеебека.
- •34. Основные типы газового разряда.
- •35. Плазма.
- •3 6. Полевая трактовка закона взаимодействия элементов тока. Опыт Ампера.
- •37. Закон Био-Савара
- •38. Сила Ампера. Сила Лоренца.
- •39. Закон полного тока. Теорема о циркуляции вектора магнитной индукции.
- •40. Магнитное поле при наличии магнетиков.
- •41. Молекулярные токи в магнетике, объемные и поверхностные токи.
- •42. Диамагнетики.
- •43. Парамагнетики.
- •44. Ферромагнетики.
- •45. Закон электромагнитной индукции Фарадея.
- •46.Энергия магнитного поля
- •47. Резонансы в цепи переменного тока.
- •48. Ток смещения. Система уравнений Максвелла.
- •49. Закон сохранения энергии электромагнитного поля.
- •50. Плоские электромагнитные волны.
12. Зависимость поляризованности от напряженности электрического поля. Влияние поляризации на электрическое поле.
Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. В постоянном или достаточно медленно меняющемся от времени внешнем электрическом поле при достаточно малой величине напряженности этого поля, вектор поляризации P, линейно зависит от вектора напряженности поля E:
![]() (в
системе СГС),
(в
системе СГС),
![]() — тензор
поляризуемости.
— тензор
поляризуемости.
![]() где
где ![]() —
три собственных числа тензора
поляризуемости. Если все эти три
собственных числа равны друг другу,
значит умножение на тензор эквивалентно
умножению на число, а среда изотропна
(в отношении поляризуемости).
—
три собственных числа тензора
поляризуемости. Если все эти три
собственных числа равны друг другу,
значит умножение на тензор эквивалентно
умножению на число, а среда изотропна
(в отношении поляризуемости).
В
достаточно сильных полях всё описанное
выше осложняется тем, что по мере роста
напряженности электрического поля рано
или поздно теряется линейность
зависимости P от E. Для
электронной и ионной поляризации при
полях, приближающихся к величинам
порядка отношения потенциала ионизации
к характерному размеру молекулы U0/D,
характерно сначала ускорение роста
вектора поляризации с ростом поля
(увеличение наклона графика P(E)),
затем плавно переходящее в пробой
диэлектрика. Дипольная (Ориентационная)
поляризация при обычно несколько более
низких значениях напряженности внешнего
поля — порядка kT/p (где p —
дипольный момент молекулы, T —
температура, k — константа
Больцмана) — то есть когда энергия
взаимодействия диполя (молекулы) с полем
становится сравнимой со средней энергией
теплового движения (вращения) диполя —
наоборот начинает достигать насыщения
(при дальнейшем росте напряженности
поля должен рано или поздно включиться
сценарий электронной или ионной
поляризации, описанный выше, и кончающийся
пробоем). Дипольные моменты стремятся
ориентироваться по направлению вектора
напряженности внешнего поля ![]() .
Поэтому вектор напряженности поля
.
Поэтому вектор напряженности поля ![]() ,
создаваемого связанными зарядами,
направлен противоположно
,
создаваемого связанными зарядами,
направлен противоположно ![]() и
ослабляет его . В результате поляризации
поле в диэлектрике ослабляется. Степень
ослабления поля зависит от свойств
диэлектрика. Напряженность электрического
поля в диэлектрике будет в ε раз меньше,
чем в вакууме.
и
ослабляет его . В результате поляризации
поле в диэлектрике ослабляется. Степень
ослабления поля зависит от свойств
диэлектрика. Напряженность электрического
поля в диэлектрике будет в ε раз меньше,
чем в вакууме.
13. Поле диполя
Р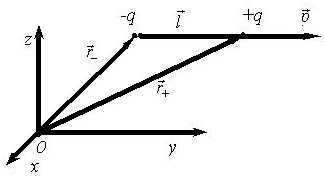
 ассмотрим
систему двух точечных электрических
зарядов
ассмотрим
систему двух точечных электрических
зарядов ![]() и
и ![]() ,
произвольным образом расположенных в
пространстве на расстоянии
,
произвольным образом расположенных в
пространстве на расстоянии ![]() друг
от друга. Такую систему зарядов назовем
электрическим диполем. Из точки
расположения отрицательного заряда в
точку расположения положительного
заряда проведем вектор
друг
от друга. Такую систему зарядов назовем
электрическим диполем. Из точки
расположения отрицательного заряда в
точку расположения положительного
заряда проведем вектор ![]() .
Электрическим моментом диполя (дипольным
моментом) назовем физическую величину
.
Электрическим моментом диполя (дипольным
моментом) назовем физическую величину
![]() .
Электрический диполь создает вокруг
себя электрическое поле, которое нетрудно
рассчитать с использованием принципа
суперпозиции. Однако на расстояниях,
значительно превышающих размер
.
Электрический диполь создает вокруг
себя электрическое поле, которое нетрудно
рассчитать с использованием принципа
суперпозиции. Однако на расстояниях,
значительно превышающих размер ![]() диполя,
электростатическое поле обладает
некоторыми характерными свойствами,
представляющими интерес для дальнейшего
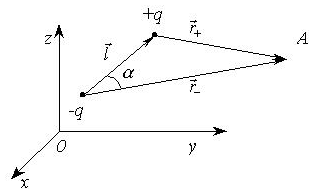
изложения предмета. Рассмотрим рис.2.
Здесь
диполя,
электростатическое поле обладает
некоторыми характерными свойствами,
представляющими интерес для дальнейшего
изложения предмета. Рассмотрим рис.2.
Здесь ![]() -
точка наблюдения,
-
точка наблюдения, ![]() и
и ![]() -
векторы, проведенные из точек расположения
соответствующих зарядов в точку
наблюдения, вектор
описан
выше. Рассчитаем значение потенциала
электростатического поля в точке
наблюдения
в
предположении, что потенциал бесконечно
удаленной точки пространства равен
нулю и
-
векторы, проведенные из точек расположения
соответствующих зарядов в точку
наблюдения, вектор
описан
выше. Рассчитаем значение потенциала
электростатического поля в точке
наблюдения
в
предположении, что потенциал бесконечно
удаленной точки пространства равен
нулю и ![]() .
Ниже под величинами
.
Ниже под величинами ![]() будем
понимать модули соответствующих
векторов. Точное выражение для потенциала
в точке
имеет
вид:
будем
понимать модули соответствующих
векторов. Точное выражение для потенциала
в точке
имеет
вид:
![]()
Векторы ![]() и
и ![]() связанны
между собой зависимостью
связанны
между собой зависимостью ![]() ,
тогда:
,
тогда:
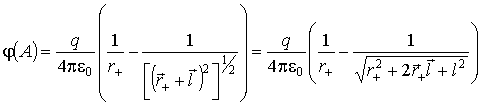 .
.
В полученном выражении опустим член ![]() как
малую величину и опустим индекс "+"
у модуля соответствующего вектора и с
учетом дипольного момента получаем:
как
малую величину и опустим индекс "+"
у модуля соответствующего вектора и с
учетом дипольного момента получаем:
![]() ,
где
,
где ![]() -
угол между вектором
-
угол между вектором![]() и
направлением на точку наблюдения
.
Заметим, что если сравнивать между собой
потенциал поля точечного заряда и
потенциал поля диполя, легко увидеть,
что потенциал поля диполя убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда.
и
направлением на точку наблюдения
.
Заметим, что если сравнивать между собой
потенциал поля точечного заряда и
потенциал поля диполя, легко увидеть,
что потенциал поля диполя убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда.
Напряженность
электростатического поля в точке
наблюдения:
 где
где ![]() ,
имеет
то же значение, что и выше.
,
имеет
то же значение, что и выше.
