8. Уравнения Лапласа и Пуассона. Вычисление напряженности поля внутри и вне заряженного цилиндра.

Уравнения Пуассона и Лапласа являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Действительно, подставляя в уравнение:

вместо величин Е_х; Е_у; Е_z их выражения через потенциал:

получаем уравнение

Это дифференциальное уравнение носит название уравнения Пуассона.

Интеграл является решением уравнения Пуассона для случая, когда заряды распределены в конечной области пространства. Если в рассматриваемой области пространства отсутствуют объемные электрические заряды, то уравнение Пуассона получает вид

и называется в этом частном случае уравнением Лапласа.

Бесконечный равномерно заряженный круглый цилиндр. Найдем с помощью уравнения Пуассона потенциал, создаваемый бесконечным круглым цилиндром радиусом а с объемной плотностью заряда ρ=const.

Направим ось Z по оси цилиндра. Вследствие аксиальной симметрии распределения заряда потенциал также аксиально симметричен, т.е. = (r). Поэтому удобно использовать цилиндрическую систему координат, аксиальный угол которой обозначим . В ней оператор Лапласа имеет вид (1)

Так как в данном случае потенциал φ зависит только от r, то выражени (1) упрощается:

(2). А уравнение Пуассона (вида ) записывается так: 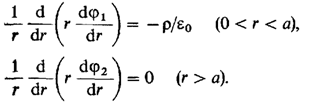(3).

Интегрируем уравнение (3) и находим постоянные интегрирования. Отсюда следует, что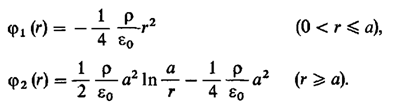 (4) Тогда 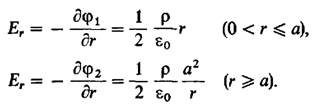(5)

Учитывая, что – заряд, приходящийся на 1 м длины цилиндра, можно второе из равенств (5) переписать в виде

Сравнение (8) и формулы напряженности, выведенной из теоремы Гаусса, показывает, что поле вне однородно заряженного цилиндра таково, как если бы весь его заряд был сосредоточен на оси.

9. Электростатическое поле при наличии проводников.

Проводниками называются материальные тела, при внесении которых в электрическое поле в них возникает движение зарядов - электрический ток. Закон, связывающий силу тока, текущего по п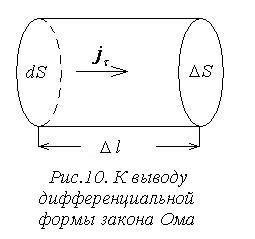 роводнику с разностью потенциалов (напряжением на его концах) имеет вид , (1) Где R-сопротивление проводника. Закон Ома в дифференциальной форме получается в результате записи соотношения (1) для плотности тока  . Рассмотрим бесконечно малый элемент проводника цилиндрической формы длины  , с сечением  , на концах которого приложена разность потенциалов  . Пусть   – удельная электрическая проводимость вещества, которая является величиной, обратной удельному электрическому сопротивлению. Тогда выражение для   можно записать в виде:  (2) , (3)

Где индекс   означает, что берется составляющая вдоль элемента проводника. Закон Ома для этого элемента записывается так:

. Полученное соотношение в векторной форме – и есть дифференциальная формулировка закона Ома.  (4). В электростатике рассматривается случай неподвижных зарядов, когда  . Из (4) следует, что  , т. е. внутри проводника при электростатическом равновесии электрическое поле отсутствует. Из уравнения   при   следует  . Это значит, что внутри проводника отсутствуют объемные заряды. Это означает, что заряд проводника концентрируется на его поверхности в слое атомарной толщины. Естественно, внутри проводника имеется как положительные, так и отрицательные заряды. Но они взаимно компенсируются и в целом внутренние области проводника нейтральны. Если нейтральный проводник внести во внешнее электрическое поле, то поверхностные заряды на нем перераспределяются, так что создаваемое ими внутри проводника поле полностью компенсирует внешнее поле, в результате чего суммарная напряженность электрического поля внутри проводника равна нулю. Явление перераспределения поверхностных зарядов на проводнике при его помещении во внешнее электрическое поле называется электрической индукцией. Если проводник заряжен, то под влиянием внешнего поля происходит также перераспределение заряда проводника.