48. Ток смещения. Система уравнений Максвелла.

Постоянный ток не протекает по цепи с конденсатором, а переменный – протекает. Сила квазистационарного тока проводимости во всех последовательно соединенных элементах цепи является одной и той же. В конденсаторе ток проводимости, связанный с движением электронов, не может существовать, поскольку обкладки разделены. В этой связи надо предположить, что между обкладками конденсатора ток протекает благодаря некоторому процессу (механизму). Этот процесс называется током смещения. Рассмотрим цепь переменного тока с плоским конденсатором. Между обкладками конденсатора имеется электрическое поле поверхностная плотность заряда на обкладке. Как известно, -заряд на каждой обкладке, S -площадь обкладки, сила тока , отсюда следует

Из локального характера этого соотношения следует ожидать его независимость от нелокальной модели (плоский конденсатор), в рамках которого оно получено. Существование тока смещения и порождение им вокруг себя магнитного поля было постулировано Максвеллом и в последующем экспериментально подтверждено другими учеными. Уравнение Максвелла с током смещения имеет вид . Добавим остальные уравнения системы Максвелла .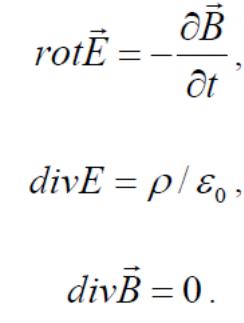

Физический смысл уравнений. Уравнение 1 выражает закон, по которому магнитное поле порождается токами проводимости и смещения, являющимися источниками магнитного поля, 2-выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле, как на один из возможных источников, порождающих вихревое электрическое поле. Вторым источником электрического поля являются электрические заряды, порождение поля которыми описывается уравнением (3), выражающим закон Кулона. Уравнение (4) говорит об отсутствии монополей – источников магнитного поля.

49. Закон сохранения энергии электромагнитного поля.

З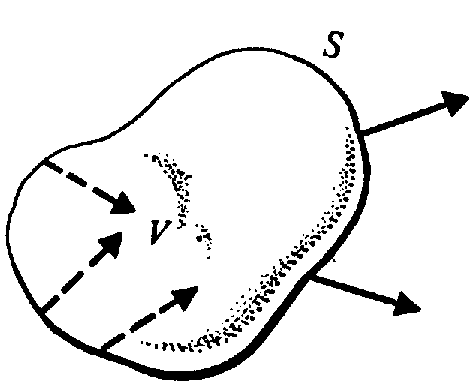 акон сохранения энергии требует, чтобы все эти процессы были сформулированы в виде закона сохранения и превращения различных форм энергии друг в друга. Поскольку при этом источники производства электромагнитной энергии пространственно отделены от мест ее потребления, возникает представление о движении энергии, характеризуемом ее потоком. Рассмотрим некоторый замкнутый объем V, в котором имеются электромагнитное поле и токи. Джоулева теплота, выделяемая токами в этом объеме, равна (1). Для упрощения расчета предполагается, что других превращений энергии в этом объеме нет. Подставляя в(1) выражения для j из уравнения , получаем (2). По формуле имеем (3), и следовательно

(4), где .

Учитывая что, и преобразуя последний интеграл в(4) по теореме Гаусса — Остроградского в интеграл по поверхности ограничивающей объем V, окончательно получаем

50. Плоские электромагнитные волны.

Электромагнитные волны излучаются лишь переменными токами и ускоренно движущимися электрическими зарядами. Постоянные токи и заряды, движущиеся равномерно и прямолинейно, не излучают. Запишем уравнение Максвелла и

Эти уравнения связывают векторы, характеризующие поле. Затем применим операцию ротора слева и справа ко второму из них, с помощью первого уравнения исключим индукцию магнитного поля. Тогда получим волновое уравнение

Исключая напряженность электрического поля, можно получить волновое уравнение для индукции магнитного поля. Решение волнового уравнения представляет собой суперпозицию плоских волн. . Такие плоские волны могут излучаться с помощью наиболее простой системы, состоящей из двух зарядов (диполь), один из которых осциллирует с частотой w . Дипольный момент такой системы изменяется со временем по закону где l - амплитуда колебаний, - единичный вектор..