5. Теорема Гаусса

Теорема Гаусса утверждает: Поток вектора напряженности электростатического поля Е через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

Д ля доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю  где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR². Следовательно, 

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R₀.

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS₀, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ₀ и ΔΦ через эти площадки одинаковы. Действительно, 

ΔΦ0 = E0ΔS0,   ΔΦ = EΔS cos α = EΔS '.

Здесь ΔS' = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.

Так как   а   следовательно   Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ₀ через поверхность вспомогательной сферы: 

Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей   точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φ_i электрических полей отдельных зарядов. Если заряд q_i оказался внутри поверхности S, то он дает вклад в поток, равный   если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю. Таким образом, теорема Гаусса доказана.

6. Потенциальность электростатического поля.

Поле, созданное кулоновскими зарядами, потенциально. Поле сил называется потенциальным, если при перемещении в этом поле работа зависит лишь от начального и конечного положения точек (тела) пути и не зависит от формы пути - траектории. Вторым эквивалентным определением потенциальности поля является условие равенства нулю работы при перемещении в нем по любому замкнутому контуру.

На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Из сказанного следует, что  , тогда условие потенциальности электрического поля

 (6.4)

(6.4) – интегральная формулировка потенциальности электрического поля.

Если заряд перемещается между точками (1) и (2), то

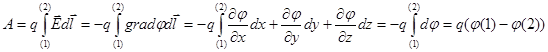 (6.8)

Если сопоставить (6.8) и (6.3), то 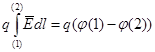 , откуда следует

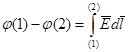
7. Скалярный потенциал.

Если воспользоваться формулой Стокса

, то из (6.4) следует дифференциальная формулировка потенциальности поля:

 (6.5)

Непосредственной проверкой можно убедиться, что

. (6.6)

Тогда сопоставляя (6.6) и (6.5) можно записать:

, (6.7) где   - некоторая скалярная функция, которая называется потенциалом. Знак «-» выбран для того, чтобы вектор напряженности Е был направлен в сторону убывания  . Скалярная функция   называется скалярным потенциалом электрического поля. Если напряженность поля можно измерить экспериментально, то потенциал   не имеет определенного числового значения и бессмысленно говорить об экспериментальном определении его значения. Потенциал определен с точностью до некоторого постоянного значения.