39. Закон полного тока. Теорема о циркуляции вектора магнитной индукции.

Для магнитного поля будем исходить из закона Био-Савара и принципа суперпозиции для магнитного поля. Их формулировка называется законом полного тока. Индукция магнитного поля, создаваемая системой токов, равна сумме индукции полей каждого тока в отдельности при отсутствии всех других: . Если контур не охватывает ток, то циркуляция равна нулю. Рассмотрим закон на произвольное количество токов в контуре. 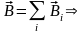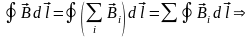Согласно принципу суперпозиции: 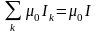, где алгебраическая сумма токов, охватываемых контуром. Итак, циркуляция магнитного поля по замкнутому контуру равна алгебраической сумме токов, охватываемой им ,умноженной на : 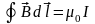(интегральная формулировка).

Дифференциальная форма закона полного тока. Для объемного тока с плотностью j:

Это значит, что его вид не зависит от того, как ведет себя плотность тока в других точках. Поэтому, хоть оно и выведено для прямолинейных токов, оно справедливо для произвольных токов. Так как магнитное поле создается не только током проводимости, но и током смещения , причем, величина поля от тока смещения равна полю от тока проводимости, то: . Закон полного тока можно представить в виде: или , где

40. Магнитное поле при наличии магнетиков.

Магнетиками называются вещества, которые при внесении во внешнее поле изменяются так, что сами становятся источниками дополнительного магнитного поля. При этом полная индукция магнитного поля равна сумме индукций внешнего магнитного поля и магнитного поля, порождаемого магнетиком. Изменение состояния магнетика под влиянием внешнего магнитного поля, в результате чего сам магнетик становится источником магнитного поля, называется намагничиванием магнетика. Это явление для широкого класса веществ было открыто экспериментально Фарадеем. Им же было установлено существование диа- и парамагнитных тел, для которых он ввел эти термины. Для исследования магнитного поля применяют магнитные стрелки (опыт Эстерда). Магнитная стрелка представляет собой магнит, одетый на остриё. При пропускании тока через проводник стрелка испытывает силовое воздействие (устанавливается перпендикулярно проводнику). 2-й метод исследования магнитного поля - с помощью плоского контура с током. Форма контура не играет роли. Необходимо, чтобы размер контура был настолько мал, чтобы не искажал исследуемое поле. Контуры, вносимые в магнитное поле, испытывают ориентирующее действие со стороны этого поля. Рамки принято характеризовать положительной нормалью. Положительной называют нормаль, проведённую к центру проводника, удовлетворяющего правилу правого винта по направлению тока. На основании действия сил на рамку делают вывод: магнитное поле - силовое и его надо характеризовать определенным направлением. За направление магнитного поля принимают направление положительной нормали в данном месте расположения контура с током.

41. Молекулярные токи в магнетике, объемные и поверхностные токи.

В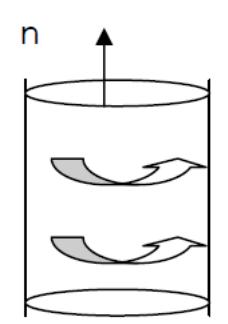 озникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, приводящие к возникновению магнитного момента требуемой величины, называются молекулярными токами. Молекулярные токи в магнетике являются объемными. При этом токи, протекающие внутри объема, взаимно компенсируют друг друга, и некомпенсированными являются только поверхностные токи. Магнитный момент такого цилиндра равен . Отсюда можно получить выражение для намагниченности через токи намагничивания где L- длина образующая цилиндром, а - поверхностный ток намагничивания тогда уравнения ротора перепишется в виде: здесь введено определение которое выражает зависимость объемного тока намагничивания от намагниченности. Используя теорему Стокса, имеем , отсюда следует , если напряженность магнитного поля.