1. Микроскопические носители зарядов. Структурные и бесструктурные частицы. Микроскопическими носителями зарядов понимают заряженные частицы и ионы. Они могут нести как положительный, так и отрицательный заряд. Известно более 200 частиц и громадное число ионов, атомов и молекул. Большая часть частиц после возникновения существует непродолжительное время, по истечении которого распадается на другие частицы. Но есть небольшое число заряженных частиц, имеющих бесконечное время жизни. Это электрон, протон и их античастицы: позитрон и антипротон. Протоны входят в состав ядер атомов, а электроны в состав электронных оболочек атомов. В состав ядер входят также и нейтроны. Они электрически нейтральны и время их жизни в составе ядер не ограничено. Заряженность ионов обусловливается тем, что в состав электронной оболочки атома или молекулы входят “лишние” электроны (отрицательные ионы), или их недостает одного или нескольких (положительные ионы). Электрон является материальным носителем элементарного отрицательного заряда  . Обычно принимается, что электрон является точечной бесструктурной частицей. Такое Масса электрона равна   кг. Протон является носителем элементарного положительного заряда  , но в отличие от электрона протон имеет внутреннюю структуру в распределении заряда. Экспериментами по взаимодействию быстрых заряженных частиц (электронов) с протонами было установлено, что электрический заряд внутри протона распределен по пространству. Внутри нейтрона также имеется электромагнитная структура. Вблизи центра нейтрона располагается положительный заряд, а дальше от центра – отрицательный. Площади, ограниченные кривыми и осью абсцисс, равны, следовательно, положительный заряд равен отрицательному, и в целом нейтрон электрически нейтрален. Отметим, что размеры областей, в которых сосредоточены электрические заряды у протона и нейтрона примерно одинаковы.

2. Элементарный заряд и его инвариантность.

П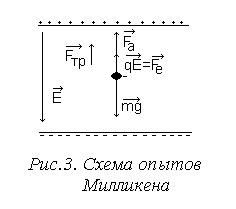 рямое экспериментальное измерение элементарного заряда было впервые выполнено Милликеном в 1909 г. Опыт Милликена.

Схема опытов Милликена изображена на рисунке.

Милликен рассматривал движение маленьких шарообразных частиц в вязкой жидкости в электрическом поле   под действием силы тяжести  , силы Архимеда  , электрической силы  и силы вязкого трения  . Уравнение второго закона Ньютона имеет вид:

+ + + =0 (1.1)

Все силы, кроме  =  могут быть измерены экспериментально при движении частицы без электрического поля. Значит из (1.1) можно найти  , а зная   найти  . Заряд частицы меняется с течением времени, что отражается на движении частицы. Найдя   и   в разные моменты времени можно найти  . Можно также изменять напряженность электрического поля и добиться, чтобы частица находилась в покое. В этом случае сила трения отсутствует, а остальные силы известны. Поэтому, зная  , можно определить  . Произведя большое число измерений зарядов, Милликен нашел, что   является всегда кратным одной и той же величине  ; т. е. Милликен установил, что  ,  , Кл. Инвариантность заряда состоит в независимости его численного значения от скорости. Фактически инвариантность доказывается фактом нейтральности атома. Из – за различий масс электрона и протона можно заключить, что электроны в атомах движутся гораздо быстрее протонов. И если бы заряд зависел от скорости, то нейтральность была бы нарушена. В настоящее время экспериментально доказана инвариантность заряда для скоростей электронов вплоть до  , где с=3 М/с – скорость света в вакууме. Нет оснований предполагать, что он не инвариантен и при более высоких скоростях. Поэтому инвариантность заряда принимается в качестве одного из экспериментальных обоснований теории электричества.

3. Закон сохранения заряда.

Закон сохранения заряда утверждает, что во время взаимодействия некоторой замкнутой системы с окружающим пространством количество заряда которое выходит из системы через ее поверхность равно количеству заряда поступившего внутрь системы. Другими словами алгебраическая сумма всех зарядов системы равна нулю.

 Как известно в природе существует два вида зарядов. Это положительные и отрицательные. Также величина заряда дискретна, то есть он может меняться только порциями. Элементарным зарядом считается заряд электрона. Если к атому добавить один электрон, то он становится отрицательно заряженным ионом. А если его отнять то положительным.

Основная идея закона сохранения заряда состоит в том, что заряд не возникает из неоткуда и не исчезает в никуда. При возникновении заряда одного знака тут же появляется заряд противоположного знака той же величины.

4. Дифференциальная формулировка закона Кулона.

Электростатическая теорема Гаусса устанавливает математическую связь между потом вектора напряженности через замкнутую поверхность и зарядами, находящимися в объеме, ограниченном данной поверхностью. Предположим, что имеется некоторый объем V, ограниченный поверхностью S и точечный заряд Q. Внутри этого объема.

Рассмотрим поток N напряженности   сквозь эту поверхность. . (5.1)

Так как Q точечный заряд. То напряженность поля равна

, (5.2). А значит

Учтем соотношение   ^

Рассмотрим сферу, на которой выделим площадку   и введем понятие телесного угла  который определим так: . (5.3)

Для бесконечно малых величин справедливо соотношение:  , и тогда из (5.1) с учетом (5.2) и (5.3) получаем:  (5.4)

Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен  (телесный угол измеряется в стерадианах: 1 стеррад = ), а поток

 (5.5)

Аналогичным образом можно посчитать поток   сквозь замкнутую поверхность, если точечный заряд находится вне объема. В этом случае, как можно показать . (5.6)

Объединяя (5.5) и (5.6) можно окончательно написать: 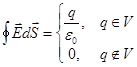 (5.7)

Утверждение, содержащееся в (5.7) и есть электростатическая теорема Гаусса для точечного заряда. Ее легко обобщить на случай, когда внутри объема находится или система точечных зарядов или непрерывно распределенный по объему заряд, используя принцип суперпозиции:

 (5.8) Или  (5.9)

Физической основой теоремы Гаусса является закон Кулона, а значит теорема Гаусса является интегральной формулировкой закона Кулона.

Воспользуемся теоремой Остроградского-Гаусса   и предположим, что в объеме V заряд распределен непрерывно с объемной плотностью  , т. е.  . Тогда  , откуда легко найти, что 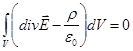 (5.10)

Ввиду произвольности объема, получаем:

 (5.11)