3. Выбор типа и порядка фильтра

Решение задачи проектирования ФВЧ можно разделить на 2 этапа:

1) Определение типа фильтра, с помощью которого можно аппроксимировать передаточную функции фильтра для получения требуемой в техническом задании АЧХ.

2) Построение принципиальной схемы фильтра и определение величин, входящих в неё элементов.

Выполнение первого этапа будем проводить для фильтра нижних частот (ФНЧ), т.к. все типы электрических фильтров (верхних частот, полосовые, заграждающие и др.) можно реализовать на основе ФНЧ-прототипа, применив соответствующее преобразование комплексной частотной переменной в передаточной функции.

I этап:

Тип фильтра необходимо выбирать исходя из следующих характеристик: частота среза (fc на рис.1), крутизна спада, минимальное затухание, максимальное затухание в полосе пропускания, минимальное затухание в полосе задерживания.

Основные типы используемых на практике характеристик являются: фильтры Баттерворта, Чебышева, Бесселя. При этом то, какой характеристикой описывается АЧХ фильтра, зависит от коэффициентов, входящих в выражение (1).

АЧХ фильтра Бесселя имеет высокую равномерность в полосе пропускания, высокую линейность ФЧХ, а недостатком является малая крутизна АЧХ.

Амплитудно-частотная характеристика фильтра Баттерворта имеет довольно длинный горизонтальный участок и резко спадает за частотой среза. В то же время линейность ФЧХ хуже, чем у фильтра Бесселя, но лучше, чем у фильтра Чебышева.

Достоинством фильтра Чебышева является высокая крутизна спада характеристики за пределами полосы пропускания, что позволяет уменьшать количество звеньев в многозвенном фильтре, а недостатком - низкая линейность ФЧХ. Кроме того, для таких фильтров характерна неравномерность (волнистость) в полосе пропускания, которая тем выше, чем больше крутизна спада АЧХ.

Так как в техническом задании нет никаких указаний по поводу неравномерностей в АЧХ, то в данном случае будет использована максимально плоская аппроксимация, которую обеспечивает фильтр Баттерворта, обладающий нулевой неравномерностью АЧХ в полосе пропускания и способный дать высокую крутизну за ее пределами. Для такого фильтра АЧХ описывается выражением:

,.

где n – порядок фильтра, чем он выше, тем круче АЧХ в переходной зоне; - относительная частота, A – коэффициент передачи (усиления) фильтра, в данном случае равен 1.

II этап:

После выбора типа фильтра необходимо опрелелиться с его порядком, который выбирается исходя из заданной крутизны АЧХ (в техническом задании: не менее 40 дБ/окт. При аппаратной реализации фильтров требуемая крутизна АЧХ за границей полосы пропускания обеспечивается каскадным (последовательным) включением нескольких фильтров, причем ввиду сложности настройки порядок фильтра каждого каскада не берется больше 2-го. При этом частоты среза отдельных звеньев будут отличаться от частоты среза всего фильтра в сборе.

Таким образом, осуществляется разложение передаточной функции на сомножители первого и второго порядков и реализация полученного разложения каскадным соединением звеньев первого и второго порядков, взаимодействие между которыми пренебрежимо мало.

Затем необходимо выбрать способ построения фильтра. Существует много способов построения активных фильтров верхних частот Баттерворта. Самые распространённые из них: схема с многопетлевой обратной связью и бесконечным коэффициентом усиления (МОС), биквадратная схема и схема на ИНУН (источник напряжения, управляемый напряжением).

С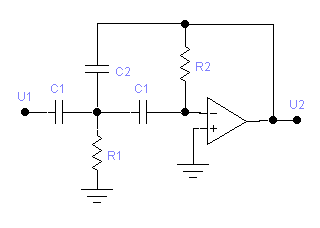 начала рассмотрим схему с многопетлевой обратной связью и бесконечным коэффициентом усиления (МОС). Она изображена на рисунке 5а.

Рисунок 5а. Схема фильтра верхних частот с МОС и бесконечным коэффициентом усиления.

Операционный усилитель в этом случае работает как прибор с бесконечным коэффициентом усиления. Эта схема реализует типовую передаточную функцию ФВЧ с инвертирующим коэффициентом усиления –К (К>0), а также не высокие значения добротности. При расчёте схемы (см. ниже) у нас получится седьмой порядок, поэтому при каскадной реализации схемы будем иметь 3 звена второго порядка и одно звено первого порядка. Следовательно, выходной сигнал получится инверсным. Недостатком этой схемы является высокая чувствительность добротности к изменению элементов (то есть невозможен большой разброс значений элементов).

Теперь рассмотрим биквадратную схему, которая изображена на рисунке 5б.

Необходимо сразу же отметить, что применение этой схемы нецелесообразно, так как она очень громоздка, а также реализует высокие значения добротности (до 100). В нашем случае максимальной добротностью обладает первый каскад (звено второго порядка). Добротность каскада определяется из его передаточной функции по формуле:

Q = b/a, где коэффициенты c и b определяются из соответствующих таблиц (см. ниже). Для звена второго порядка ФВЧ Баттерворта они равны: b = 1; a = 0,4450. Следовательно, максимальная добротность равна 2,25 (намного меньше 100).

Р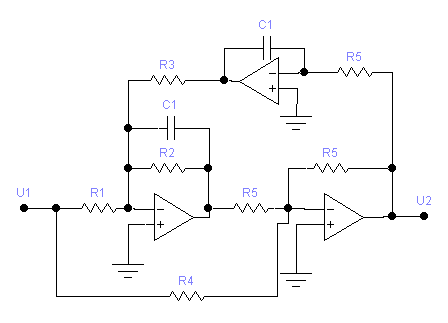 исунок 5б. Схема биквадратного фильтра верхних частот.

О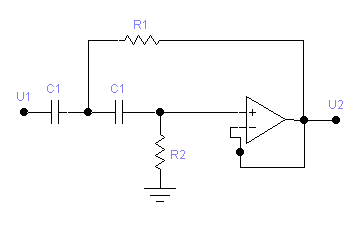 собенности рассмотренных схем определили выбор третьей схемы - на ИНУН, которая изображена на рисунке 5в.

Рисунок 5в. Схема фильтра верхних частот на ИНУН.

Эта схема реализует неинвертирующий (т.к. порядок фильтра нечётный) коэффициент усиления К>0 при минимальном числе элементов. При реализации схемы на ИНУН требуется на один резистор больше, чем для фильтра с МОС, он обладает низким выходным сопротивлением (что позволяет его сразу соединять каскадно с другими звеньями для реализации фильтра более высокого порядка), небольшим разбросом значений элементов. Также этот фильтр относительно прост в настройке. Подобно фильтру с МОС фильтр на ИНУН используется для значений добротности Q<=10. При К=1 ИНУН работает как повторитель напряжения.