Курсовая работа

На тему

«Фильтр высоких частот»

Выполнила студентка

гр. 3092/2

Казанцева М.А.

Преподаватель

Уткин М.А.

Содержание

1. Вводная часть……...……………………………………………………………………..3

2. Фильтр высоких частот.............…………………………………………………………4

3. Выбор типа и порядка фильтра........................................................................................8

4. Выбор структуры фильтра……………………………………………………...….......12

5. Техническое задание.......................................................................................................12

6. Расчёт схемы....……………………………………….……………………………...…12

7. Принципиальная схема фильтра верхних частот…………………..……………..….16

8. Результаты моделирования…………………………………………………………….16

1. Вводная часть.

Фильтром называется электронная схема, пропускающая или усиливающая синусоидальные сигналы в определенном диапазоне частот и ослабляющая сигналы с частотами, выходящими за пределы заданного диапазона.

Область применения фильтров в электронике и вычислительной технике очень широка и схемы отличаются большим разнообразием. Простые пассивные фильтры строятся на резисторах, конденсаторах и катушках индуктивности. Более сложные, активные - на базе операционных усилителей и цепей из резисторов и конденсаторов.

Основной характеристикой фильтра считается его амплитудно-частотная характеристика (АЧХ), отображающая зависимость коэффициента передачи фильтра K(ω) от угловой частоты сигнала ω. По виду АЧХ устройства обычно разделяются на группы.

Например, фильтр низкой частоты (ФНЧ) пропускает низкочастотные сигналы и ослабляет высокочастотные (рис.1а), фильтр высокой частоты (ФВЧ) пропускает сигналы высокочастотные и ослабляет низкочастотные (рис.1б).

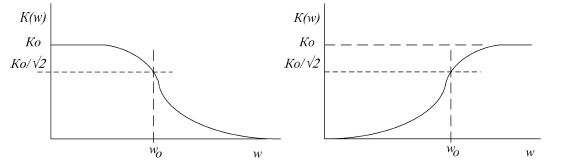
Рис.1.Амплитудно-частотная характеристика(а - фильтр низкой частоты, б - фильтр высокой частоты).

Для описания ФНЧ и ФВЧ вводится понятие частоты среза ω₀ - частоты сигнала, на которой наблюдается уменьшение мощности в 2 раза. Коэффициент передачи фильтра при этом уменьшается в раз по сравнению с коэффициентом передачи K₀ на нулевой (для ФНЧ) или на бесконечной (для ФВЧ) частоте.

Проектирование фильтра основывается на расчете его передаточной функции:

W(p) = Uвых(p)/Uвх(p), где Uвых(p) и Uвх(p)- выходное и входное напряжения.

Для перехода от передаточной функции к частотным характеристикам производят замену p = j*ω, где j= .

Передаточную функцию можно представить в виде комплексного выражения, содержащего вещественную A(ω) и мнимую B(ω) части:

W(j*ω) = A(ω)+j*B(ω), или в показательной форме W(j*ω)=K(ω) *e ^j*φ(ω) ,

где: K(ω) и φ(ω) - соответственно, модуль и аргумент комплексной величины, указывающие величину и направление вектора W(j*ω) на комплексной плоскости.

Модуль передаточной функции K(ω)=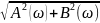 является описанием АЧХ фильтра, а аргумент φ(ω)=arctg описывает его фазочастотную характеристику (ФЧХ).

Из-за большого диапазона изменения коэффициента передачи фильтра его значение обычно логарифмируется и умножается на 20. Это позволяет измерять K(ω) в децибелах.

а = -20*log10(|W(j* ω) |), и в этом случае а характеризует затухание.

Частота ω (рад/с) связана с частотой f (Гц) соотношением: ω = 2πf.

Диапазон частот, в котором сигналы проходят, называются полосами пропускания (значение АЧХ в них велико). Диапазон частот, в котором сигналы подавляются, образуют полосы задерживания (значение АЧХ в них мало). Интервал частот, в котором характеристика постоянно спадает, переходя от полосы пропускания к полосе задерживания, называется переходной областью.

На практике невозможно реализовать идеальную характеристику, так как нужно сформировать очень узкую переходную область. В практическом случае полосы пропускания и задерживания должны быть формально определены. В качестве полосы пропускания выбирается диапазон частот, где значение АЧХ превышает некоторое заранее выбранное число, а полосу задерживания образует диапазон частот, в котором АЧХ меньше определённого значения (уровень –3 Дб).

Реальные АЧХ оказываются лучше для фильтров более высокого порядка, но повышение порядка связано с усложнением схемы, поэтому часто задача состоит в получении характеристики, наиболее близкой к идеальной (с заданной точностью) при наименьших затратах и сложности реализуемой схемы.