5. Кинематический анализ.

Целью кинематического анализа является определение скоростей и ускорений отдельных точек и звеньев рычажного механизма по известному закону входного звена.

Путём дифференцируя уравнения дважды по q уравнения геометрического анализа, находятся аналоги скоростей и ускорений данного механизма.

5.1 План скоростей и ускорений

Рис.5.1. Положение механизма при 30°

1. Сумму векторов можно представить как :

2. Производная по времени от каждого полученного векторного уравнения:

3. Полученные выражения можно представить в виде:

_{4. Построение плана скоростей:}

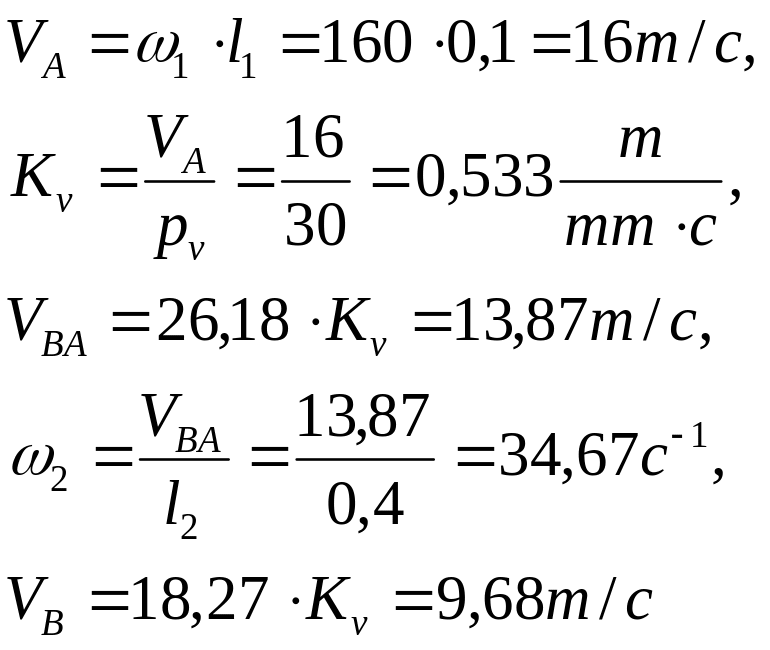
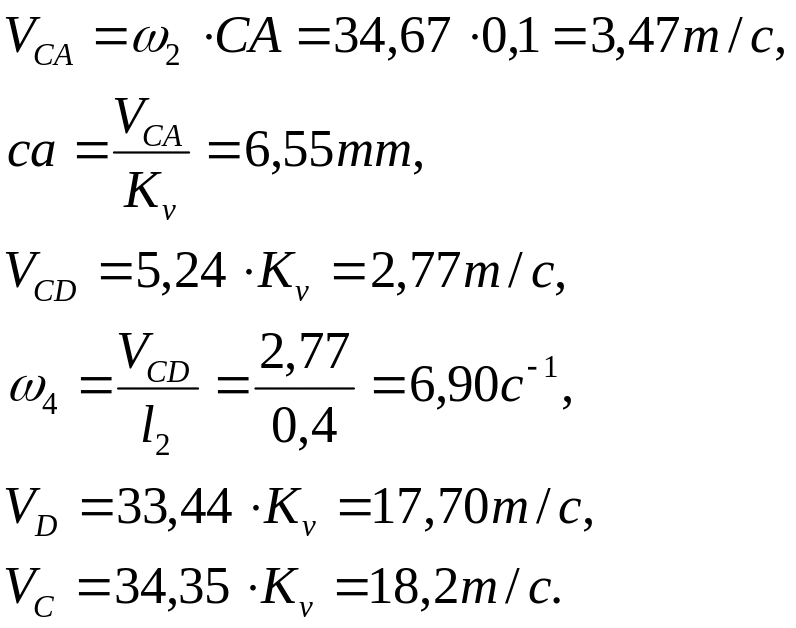
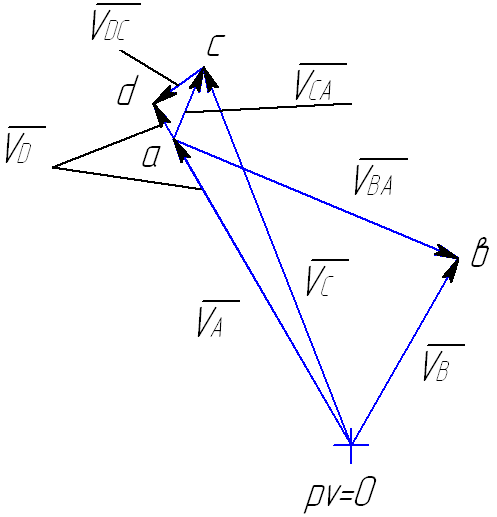
Рис.5.2. План скоростей для положения 30°

1. Производную по времени от каждого полученного векторного уравнения:

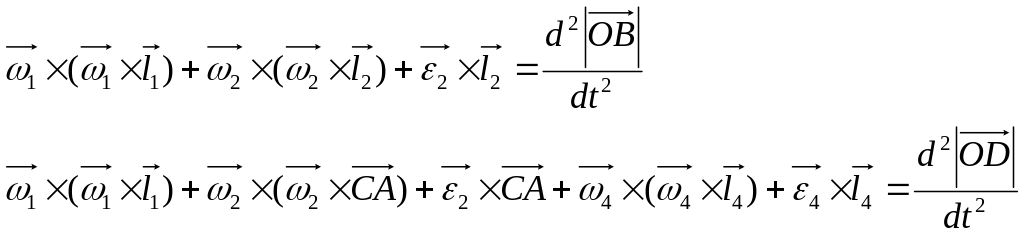
2. _{Полученные выражения можно представить в виде:}

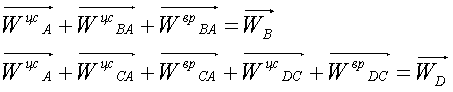
_{4. Построение плана ускорений:}

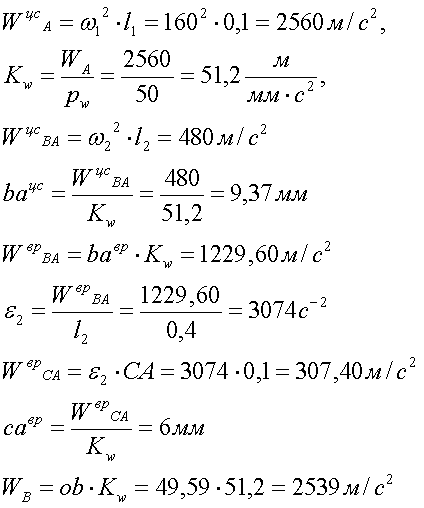
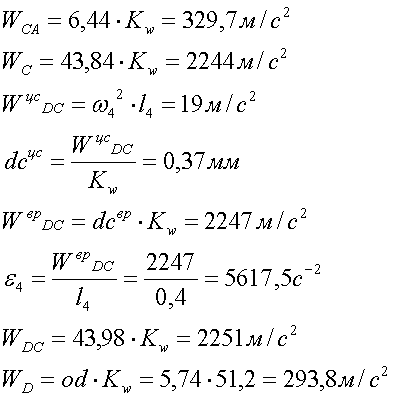
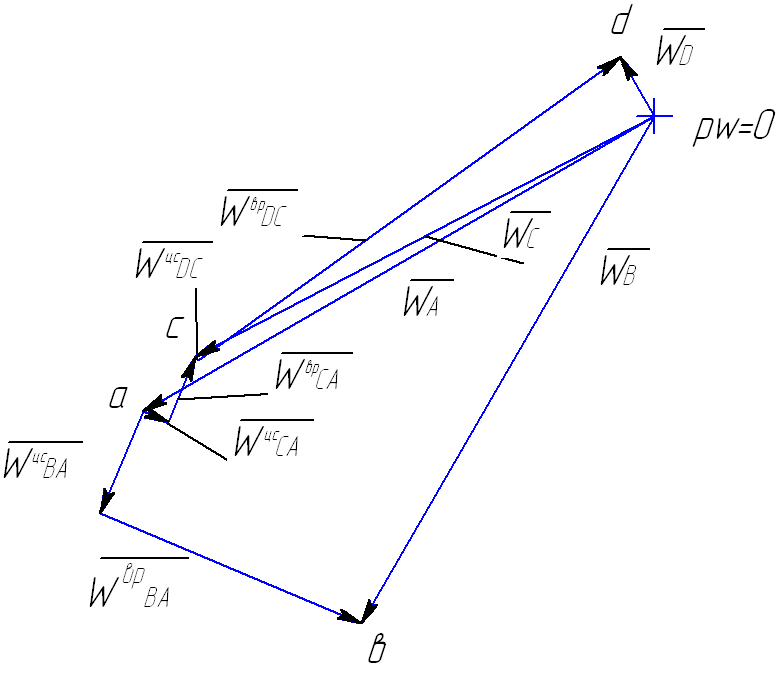
Рис.5.3. План ускорений для положения 30°

_{Аналогично для крайнего положения.}

_{Построение плана скоростей:}

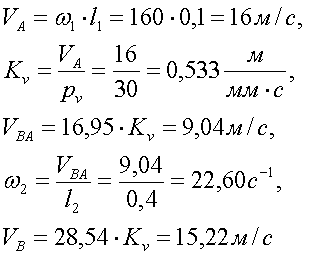
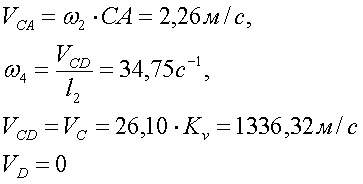
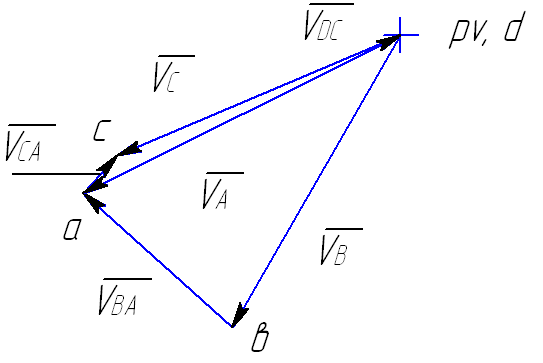
Рис.5.4. План скоростей для крайнего положения

_{Построение плана ускорений для крайнего положения:}

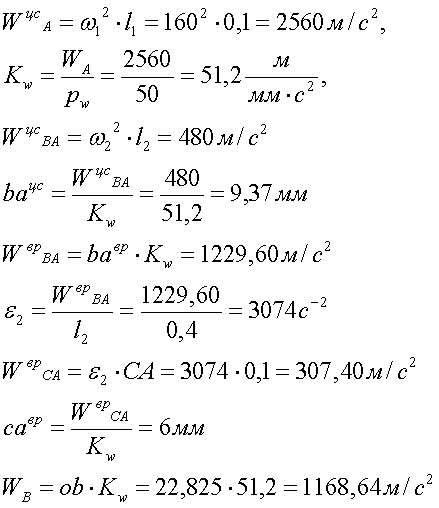
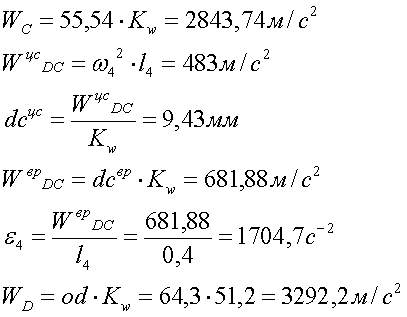
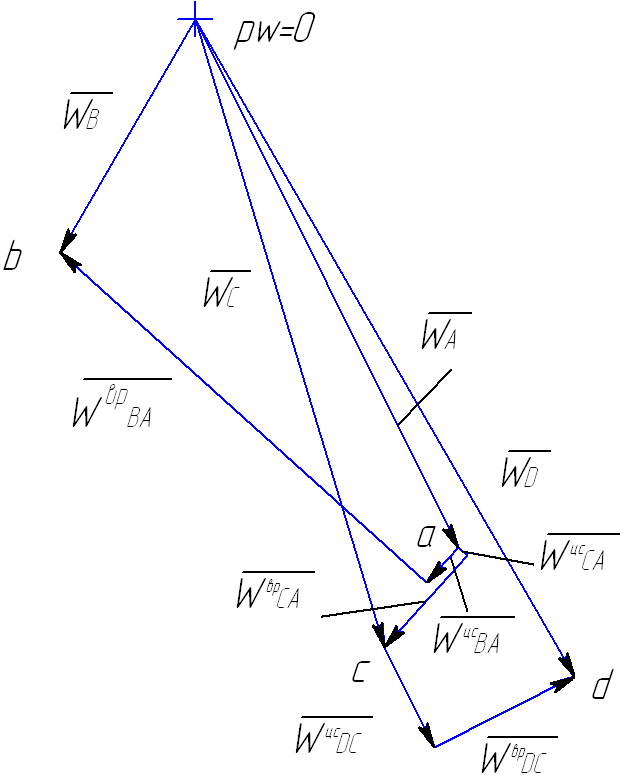
Рис.5.5. План ускорений для крайнего положения

5.2 Аналитическое определение аналогов скоростей и ускорений.

А) Для определения аналогов скоростей берутся первые производные от групповых уравнений по обобщённой координате (q), для первой группы:

, (5.1)

Корни уравнений находятся по метод Крамера:

, (5.2)

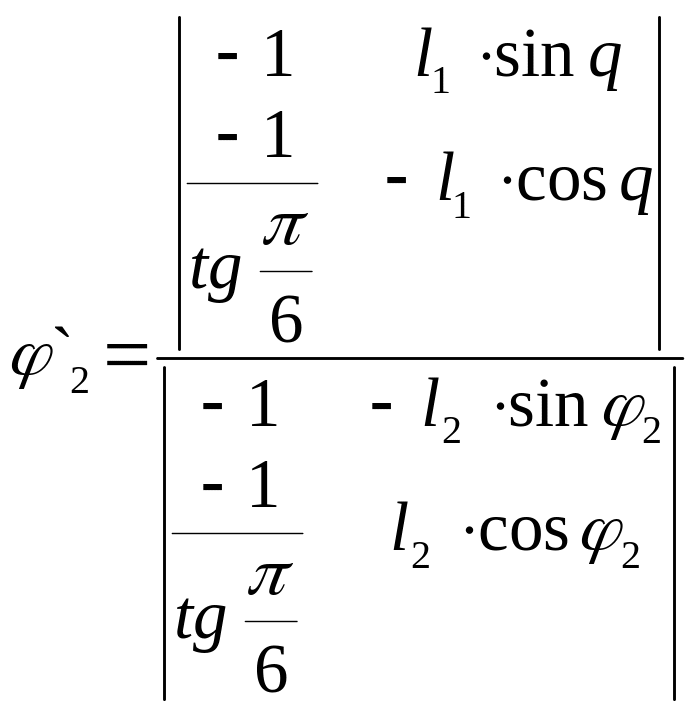. (5.3)

Решение в общем виде:

– аналог скорости точки В, (5.4)

– аналог угловой скорости звена 2. (5.5)

Значение аналога скорости точки В и аналога угловой скорости звена 2 при входной координате q=30°:

x`_в= 0,03 ,

φ`₂= – 0,218 .

Б) Аналогичный расчёт производится для второй группы:

, (5.6)

Корни уравнений находятся по метод Крамера:

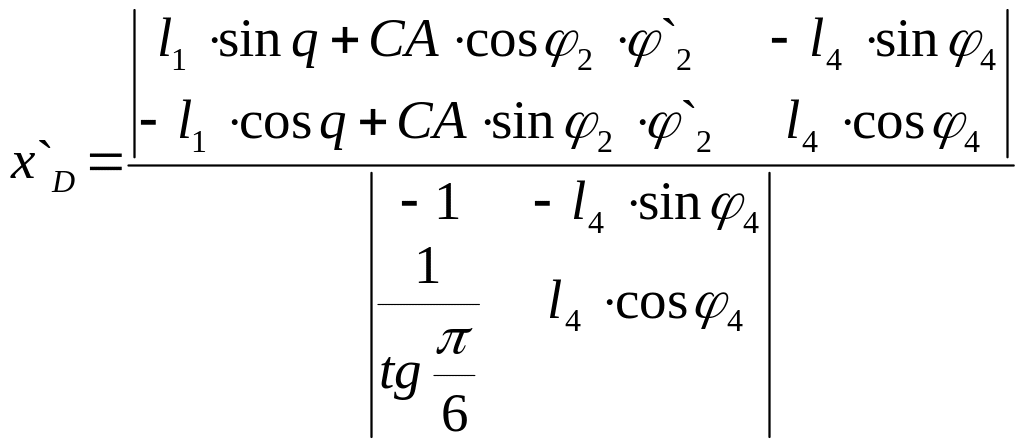, (5.7)

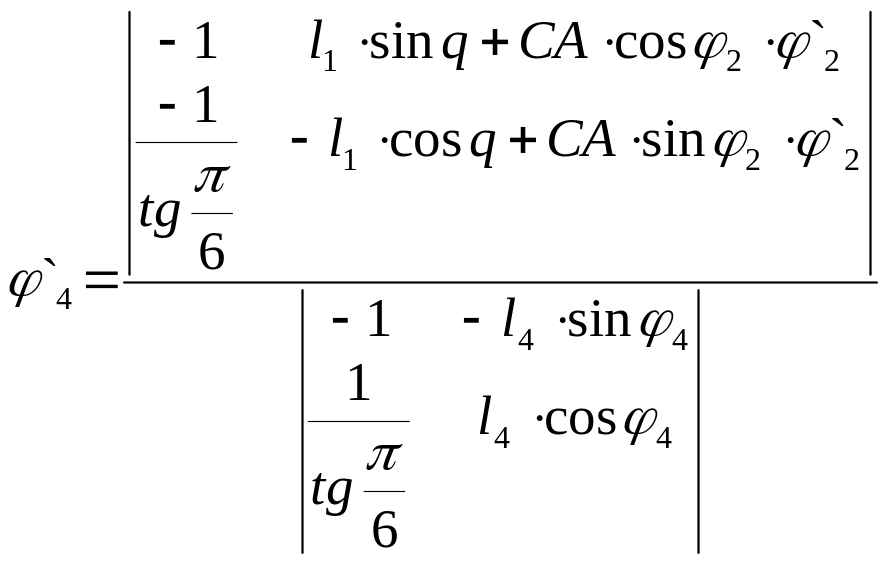. (5.8)

Решение в общем виде:

– аналог скорости точки D, (5.9)

– аналог угловой скорости звена 4. (5.10)

Значение аналога скорости точки В и аналога угловой скорости звена 2 при входной координате q=30°:

x`_D= –0,056 ,

φ`₄= 0,044 .

В) Для определения аналогов ускорений берутся вторые производные от групповых уравнений по обобщённой координате (q), для первой группы:

, (5.11)

Корни уравнений находятся по метод Крамера:

, (5.12)

. (5.13)

Решение в общем виде:

– аналог ускорения точки В, (5.14)

– аналог углового ускорения звена 2. (5.15)

Значение аналога ускорения точки В и аналога углового ускорения звена 2 при входной координате q=30°:

x``_в= -0,05 ,

φ``₂= – 0,12 .

Г) Аналогичный расчёт производится для второй группы:

,(5.16)

Корни уравнений находятся по метод Крамера:

, (5.17)

. (5.18)

Решение в общем виде:

– аналог ускорения точки D, (5.19)

– аналог углового ускорения звена 4. (5.20)

Значение аналога ускорения точки D и аналога углового ускорения звена 4 при входной координате q=30°:

x``_D= 5697 ,

φ``₄= – 5627 .

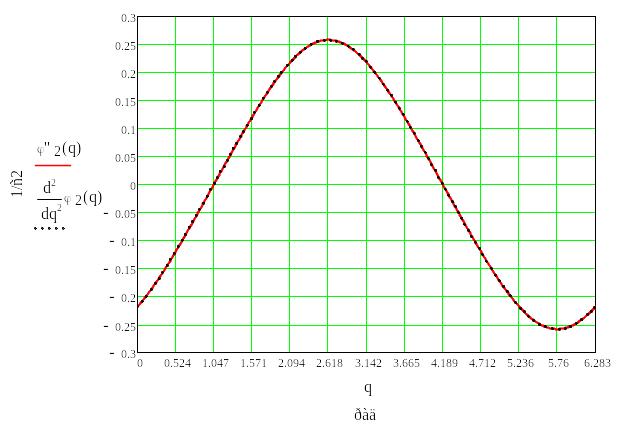
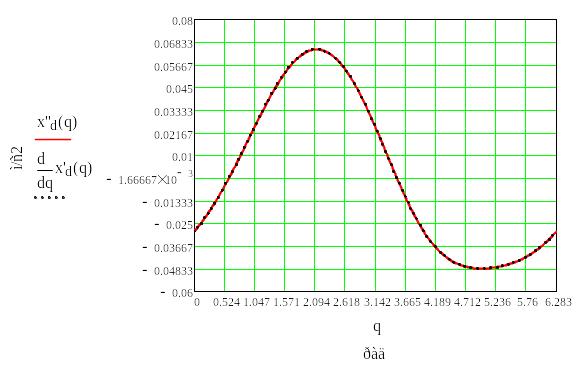
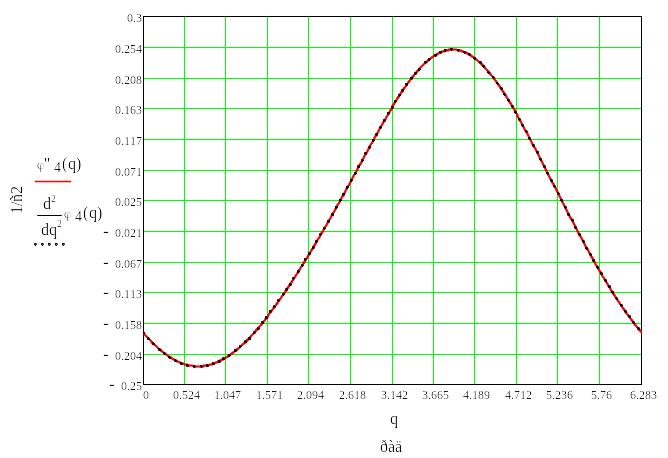
6. Графики функции положеия и её производных по обощённой координате.

Полученные графики являются совмещенными графики производных функций положения и функций, полученных раскрытием определителей.

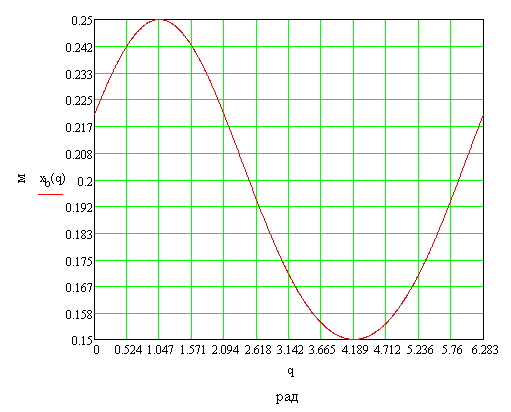
Рис.6.1. График функции положения х_в

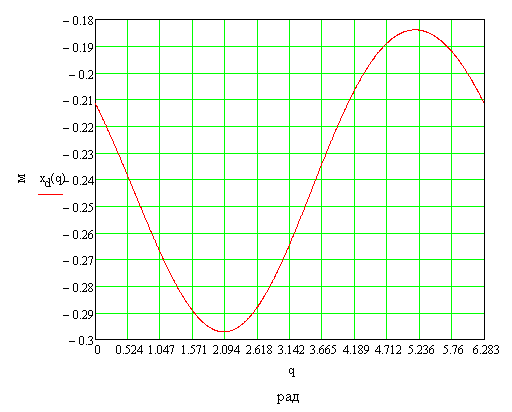
Рис.6.2. График функции положения x_D

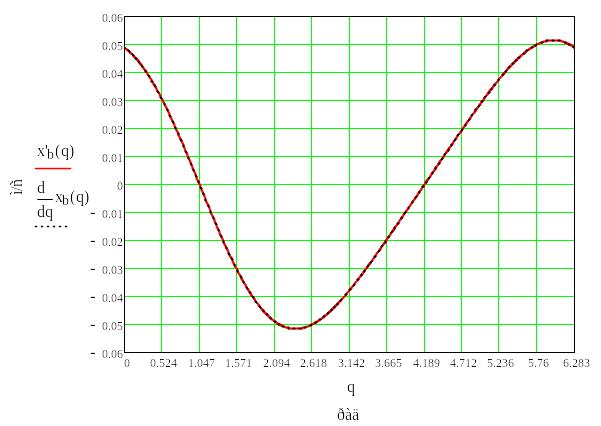
Рис.6.3. График производной функции положения точки В

Рис.6.4. График угловой скорости звена 2

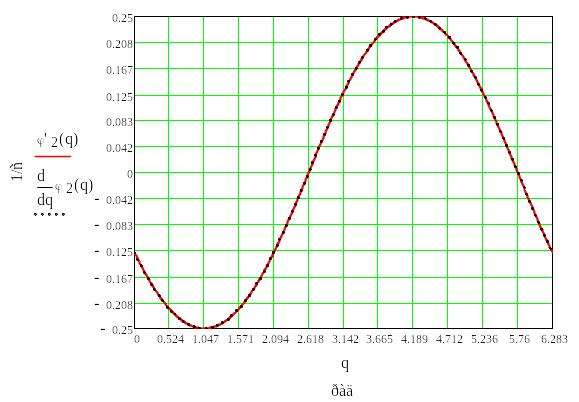
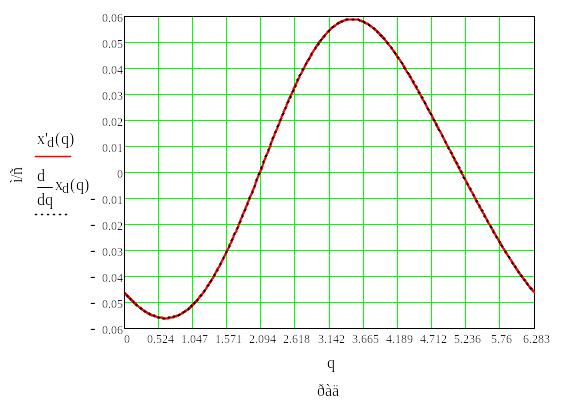
Рис.6.5. График производной функции положения точки D

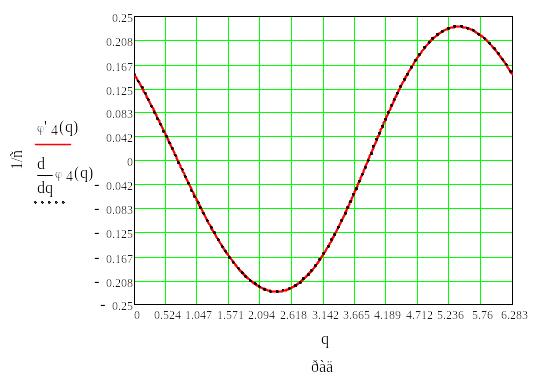
Рис.6.6. График угловой скорости звена 4

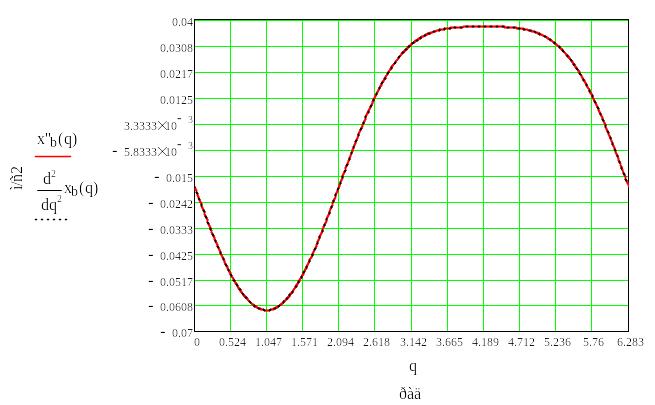
Рис.6.7. График второй производной функции положения точки В

Рис.6.8. График углового ускорения звена 2

Рис.6.9. График второй производной функции положения точки D

Рис.6.10. График углового ускорения звена 4