7.3.4. Начало европейской математики и физики

К этому же периоду относится появление в Европе первого самостоятельного средневекового математика Леонардо Фибоначчи (1170 – 1228), который уже не был просто комментатором и компилятором античных авторов. Будучи сыном крупного купца и путешественника из Пизы, он и сам много ездил по торговым делам на Восток, встречался с мусульманскими учеными, знакомился с их манускриптами. Там он заинтересовался десятичной системой счисления (в Европе, несмотря на усилия Боэция и Герберта, она еще оставалась практически неизвестной), оценил ее удобство и эффективность, освоил её и после этого опубликовал «Книгу абака» (1202 г.). В ней он подробно изложил эту систему, продемонстрировав ее преимущества перед господствовавшей римской системой. Этим вопросам посвящены 7 из 15 глав этой книги. В них после общего описания десятичной позиционной системы излагаются арифметические операции с целыми числами и обыкновенными дробями. В главах 8 – 10 даются приложения к коммерческим расчетам и решается множество конкретных задач. В 11 – 12 главах проводится суммирование арифметических прогрессий и квадратов натуральных чисел, а также ищутся целочисленные решения линейных неопределенных уравнений. Глава 14 посвящена вычислению квадратных и кубических корней и действиям с биномами. Завершается книга главой, в которой дается краткое изложение алгебры, близкое к результатам ал-Хорезми, а также рассматриваются геометрические задачи на теорему Пифагора.

Нужно признать, что «Книга абака» – первое в средневековой Европе математическое сочинение, содержащее ряд новых и оригинальных результатов, выходящих за пределы античного знания. В силу своего прикладного характера она стала наглядным учебником для купцов, банкиров, строителей и прочих профессионалов, связанных с расчетами и логистикой. Фибоначчи первый продемонстрировал удобство действий с отрицательными числами (которые он трактовал как «долг» в экономических расчетах) и действий с дробями, а также ввел нуль как одну из обычных цифр. И надо признать, что это было поистине революционное нововведение, т.к. оно радикально упрощало бухгалтерию, счётные процедуры необходимые купцам и финансистам, а также сыграло важнейшую роль в подъёме точных наук и интеллектуального мышления. Однако средневековое массовое мышление активно сопротивлялось этому новшеству и, как пишет Ч. Сейф, автор книги «Биография цифры нуль», «Нуль часто ненавидели, издавна боялись, а то и запрещали». Из-за этого судьба нуля оказалась весьма сложной и запутанной, а его окончательное признание и распространение произошло только в XVIII веке.

Увлекшись математикой, Фибоначчи в 1220 г. выпустил учебник «Практическая геометрия», где дал расчет площадей многоугольников, круга, поверхностей сферы и цилиндра, доказал формулу Герона и описал свойства медиан треугольника. Здесь же он излагает свой способ нахождения числа π, для которого получает значение π=3,1418.

Последняя его «Книга квадратов» (1225) посвящена изучению бесконечных числовых последовательностей, где он впервые столкнулся с тем удивительным фактом, что сумма части бесконечной последовательности (например, ряд 1²+2²+3²+…) может быть равна всей этой последовательности! Там же он открыл и свой знаменитый «ряд Фибоначчи»:

0, 1, 1, 2, 3, 5, 8, 13, 21,…, (7.1)

в котором каждый член ряда является суммой двух предыдущих. Этот ряд он получил как решение следующей предложенной им задачи: «Сколько пар кроликов может народиться от одной пары в течение года, если: а) каждая новая пара, начиная с месяца со дня рождения, производит ежемесячно новую пару; б) кролики не дохнут». Постепенно выяснилось, что ряд (7.1) обладает множеством интересных свойств и тесно связан со знаменитым «золотым сечением». Действительно, из его рекуррентной записи u_n=u_n-1+u_n-2 (это, кстати, первое в математике рекуррентное соотношение), представляющей собой, линейное конечноразностное уравнение второго порядка, нетрудно получить общее решение u_n=aqⁿ , где a- произвольная константа, а q- корень квадратного уравнения q²-q-1=0, равный . Полагая, что u₁=u₂=1, приходим к известной формуле Бине для чисел Фибоначчи, полученной им в 1843 г и названной его именем, (хотя еще в 1728 г она была опубликована знаменитым швейцарским математиком Д. Бернулли):

(7.2)

Здесь фигурирует «золотая пропорция» , , играющая уникальную роль в природе, искусстве, технике и т.д. Как показал впоследствии И.Кеплер, к золотой пропорции стремится и отношение двух соседних чисел ряда (7.1), а именно

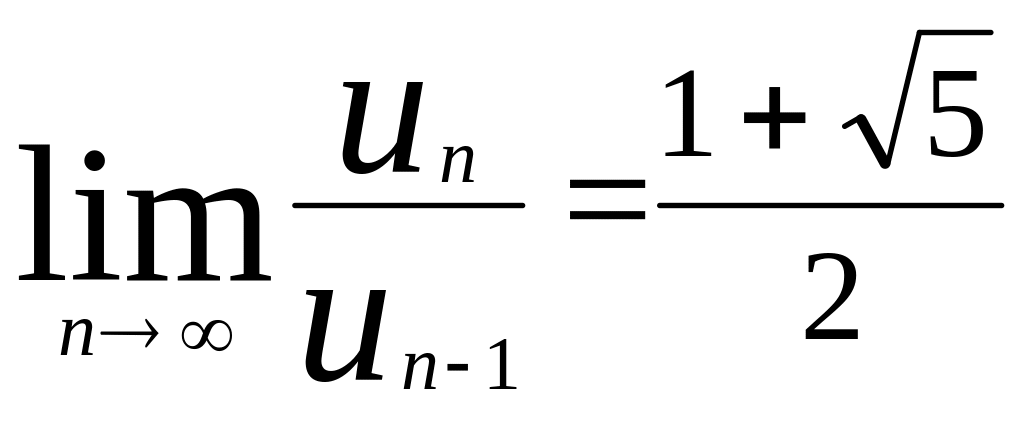(7.3)

Если в качестве начальных значений u₁ и u₂ выбрать не единицы, а иные целые числа, то придём к т.н. «обобщенным числам Фибоначчи». Их частным случаем являются «числа Люка», которым отвечает выбор u₁=1, u₂=3 и которые также обладают рядом интересных свойств. Также в своей книге Фибоначчи обобщил теорему Пифагора на случай диагонали параллелепипеда и рассмотрел способы решения неопределенных (целочисленных) квадратных уравнений, продолжая построения Диофанта. В частности он обсуждает и будущую Великую теорему Ферма xⁿ+yⁿ=zⁿ для случая n=4. Разумеется, наибольшим спросом в то время пользовалась первая из названных книг Фибоначчи, будучи необходимой как купцам, так и студентам и преподавателям университетов. Тем не менее общее число рукописных копий этой книги по оценкам историков вряд ли намного превосходило сотню.

Работы и идеи Фибоначчи стали катализатором европейской математики, механики и физики, и по его следам пошли многие его современники и продолжатели. Исследования по механике стали развиваться по трем направлениям: статика, кинематика и связь «импетуса» с падением тел. Одним из первых исследователей проблем статики был французский физик и математик, генерал Доминиканского ордена, профессор Парижского университета Иордан Неморарий (? – 1237). На основе трактатов Никомаха и Боэция он написал «Арифметику, изложенную в десяти книгах», книгу «О данных числах», трактаты «О сфере» и «О треугольниках», где начал систематическое использование букв вместо неизвестных чисел. Наглядное изложение своей системы обозначений он дает на примерах решения 115 задач, сводящихся к линейным и квадратным уравнениям (трактат «О данных числах» в 4-х томах). Его же можно считать первым средневековым механиком-теоретиком, т.к. в своем трактате «Об отношении тяжестей» он фактически использует понятие момента силы и с его помощью решает задачу о равновесии тела на наклонной плоскости. Обсуждая влияние сил сопротивления на движение тела в воздухе, заключает, что они тем меньше, чем тело острее и глаже. Изучая движение и равновесие рычага, вплотную подходит к формулировке «золотого правила механики», замечая, что уменьшение поднимаемого груза в n раз позволяет увеличить высоту его подъема также в n раз. Это свойство рычага он характеризует как «тяжесть, соответственно положению». Впервые он рассматривает и ломаный (коленчатый) рычаг, хотя и не все его выводы о равновесии оказались верными. Трактат «Об отношении тяжестей» оказал большое влияние на развитие теории простых машин. Он переиздавался в Европе на протяжении более 200 лет, став хорошо известным таким титанам Возрождения, как Н. Тарталья, Дж. Бенедетти, Г. Галилей, Л. да-Винчи.

Важную роль в подъеме интереса к механике в Европе сыграли и первые переводы на латынь трактатов Архимеда «О равновесии плоских фигур» и «О плавающих телах», сделанные в 1269 г В. Мербеке. Эти работы впервые за 1,5 тыс. лет вновь привлекли внимание ученых к вопросам гидростатики (А. Саксонский, И. де Мурис, Н. Кузанский), результаты которых были позднее подытожены замечательными исследованиями Г. Галилея и С. Стевина.

Принципиально новым направлением в европейской механике XII – XIII вв. стало появление исследований по кинематике. Здесь в первую очередь следует упомянуть трактат Герарда Брюссельского (XII – XIII в.) «О движении», в котором впервые появляется понятие переменной скорости движения и даже ее среднего значения. Наиболее же серьезные результаты оксфордской школы по изучению свойств механического движения были продемонстрированы в «Трактате о пропорциях скоростей в движении», написанном в 1328 г. кентерберийским архиепископом Томасом Брадвардином (1290 – 1349), английским математиком и механиком, родоначальником Оксфордской («Мертонской») школы. В нем автор вводит понятия ускорения и замедления движения, а также понятие мгновенной скорости в каждый момент времени как для кругового, так и для прямолинейного движения. Брадвардин различает понятия «качество движения» и «количество движения», понимая под первым из них скорость, а под вторым – продолжительность. Помимо кинематических построений он пытается отделить «силу сопротивления» от «силы движения», понимая под первой силу «инерционного» сопротивления. Считая движущую силу F источником движения, а R – сопротивлением, приходит, к следующей формуле для связи скорости V с силой V = logF/R (которую определяет словесно). В области математики он известен своей книгой «Умозрительная геометрия», в которой приводит ряд теорем о звездчатых многоугольниках и обсуждает их изопериметрические и экстремальные свойства. Переходя к правильным многогранникам, впервые ставит задачу о заполнении ими пространства. В своем последнем «Трактате о континууме» (1335) обсуждает вопросы математической непрерывности, дискретности, бесконечности и т.д. В области практической математики мы обязаны ему введением функций ctg и tg , а также термина «иррациональность».

Дальнейшее развитие кинематика получила в работах учеников Брадвардина – ученых Мертон-колледжа Оксфордского университета, уточнивших и развивших основные понятия кинематики неравномерных движений. Эти понятия сыграли важную роль при открытии законов динамики. К этому же времени относится формулировка знаменитого «принципа простоты», получившего наименование о «бритвы Оккама»: «Не следует сущности умножать без необходимости», сделанная францисканским монахом Уильямом Оккамом (1285 – 1349). Хотя этот принцип был предложен им для упрощения богословской аргументации, со временем выяснилась его высочайшая эффективность в научных спорах и поисках. В ХХ веке Эйнштейном была предложена изменённая форма этого принципа: «Всё следует упрощать до тех пор, пока это возможно, но не более того». В современной механике и физике это утверждение стало основной идеей т.н. «асимптотологии», – идеологии построения упрощённых математических моделей, учитывающих роль лишь ведущих факторов изучаемой системы. За счёт этого модель становится более «прозрачной» и пригодной для верификации и последующего анализа.

Независимо от Оксфордской школы, в Сорбонне также шел процесс изучения свойств и характеристик механического движения. Наибольшую известность здесь приобрели идеи и результаты двух сорбоннских профессоров – Ж.Буридана и Н.Орема.

Жан Буридан (1300 – 1358), ректор Сорбонны и вместе с тем крупный французский ученый XIV в., живо откликнулся на критику Аристотелевых идей о причинах движения, высказанную оксфордскими учеными, и занялся самостоятельным исследованием этой проблемы. В трактате «Вопросы к восьми книгам «Физики» Аристотеля» он прямо говорит: «Аристотель, как мне кажется, неправильно решил эту задачу». Свои умозаключения Буридан строит на обсуждении разнообразных примеров механического движения. Так, рассматривая вращающийся волчок или точильный камень, он справедливо заключает, что здесь не образуется пустоты и поэтому воздух никак не может подталкивать вращающееся тело, что противоречит утверждениям Аристотеля. При обсуждении движения брошенного копья Буридан резонно заключает, что копье с заостренным задним концом летит столь же хорошо, как и копье с затупленным, хотя согласно Аристотелю второе должно было бы лететь лучше. Отсюда Буридан делает важный вывод, что движущееся тело несет в себе некоторый «напор» (impetus), который постепенно уменьшается из-за внешнего сопротивления, отчего тело в конце концов падает вниз. При этом у тяжелого и плотного тела приобретаемый им при броске импетус больше, чем у легкого. Обсуждая процесс отскока упругого мяча от стенки Буридан поясняет, что в процессе его упругой деформации импетус сначала уменьшается, однако затем вновь самообразуется, заставляя мяч двигаться в другом направлении. Аналогично происходит колебание натянутой струны. Обращаясь к примеру свободно падающего тела, скорость которого непрерывно растет, Буридан считал, что оно увеличивает свой импетус за счет действия так называемой «силы импетуса» или «акцидентальной тяжести», вызывающей рост скорости.

Из сказанного видно, что Буридана можно считать основоположником теории импетуса, хотя само это понятие еще оставалось крайне расплывчатым. Оно, по существу, объединяло в себе такие современные характеристики, как скорость движения тела, его масса, его энергия, его импульс. Свойство сохранения импульса тела при отсутствии сил сопротивления является прообразом свойства инерции, введенного в науку 300 лет спустя в работах И. Кеплера, Г. Галилея, И. Ньютона.

Вращения небесных сфер Буридан уподобляет вращению точильного камня, говоря, что Всевышнему нет необходимости непрерывно их вращать, как полагал Аристотель, а достаточно лишь сообщить им некоторый начальный импетус. В этом утверждении также содержится идея о свойстве инерции материальных тел. Из этого можно заключить, что Буридан пытался сделать математику основой научного богословия, положив начало длинной цепи аналогичных попыток, продолжающихся до настоящего времени.

Имя Буридана приобрело широкую известность еще и в связи с предложенным и изученным им логическим парадоксом о так называемом «Буридановом осле», который, будучи голодным, не мог выбрать одну из двух симметрично расположенных перед ним кормушек в силу их абсолютной равнозначности, и в результате умер с голоду. Этот парадокс наглядно демонстрирует тот факт, что в симметричной задаче решение может быть несимметричным. Поставленная здесь проблема аксиомы выбора была полностью осознана и изучена математиками только в XIX в. при разработке теории множеств.

Талантливым учеником и последователем Буридана стал профессор Сорбонны и советник короля Карла V Никола Орем (1323 – 1382). По поручению короля он сделал перевод на французский нескольких сочинений Аристотеля, снабдив их своими комментариями. Независимо от ученых Оксфордской школы (хотя и несколько позже их) он ввел понятие средней скорости при равноускоренном движении и фактически подтвердил «мертонское правило»: путь, пройденный телом при ускоренном движении, равен пути, пройденному им за то же время при равномерном движении со средней скоростью. Это утверждение стало последней ступенькой к будущему открытию Галилея: путь пройденный при ускоренном движении пропорционален квадрату времени. В «Книге о небе и Вселенной» (1377) он активно поддерживает и развивает высказывания Буридана о возможности суточного вращения Земли, выступая с критикой античных заблуждений на этот счет. В конце книги Орем, обращаясь к молодежи, советует ей «чтобы она училась противоречить и поправлять авторов ради любви и стремления к истине».

Большой вклад был им сделан в математику. В трактате «О конфигурации качеств» (1371) он впервые вводит понятие дробного показателя степени (на примере 4^3/2), а также использует прямоугольные координаты, откладывая параллельно «вертикальной» оси отрезки, пропорциональные скорости, а по «горизонтальной» – пропорциональные времени. Соединяя верхние концы отрезков некоторой «линией верхнего края», Орем фактически строил график зависимости скорости от времени в т.н. «декартовых координатах» (на 300 лет раньше Декарта). Заинтересовавшись убывающими последовательностями, Орем обнаружил сходимость БУГП (что было известно еще Архимеду) и задался вопросом о сходимости гармонического ряда (1/n) и ряда обратных квадратов (1/n²). Для гармонического ряда он доказал его расходимость, собирая его члены в группы, сумма которых превышает 1/2:

(7.4)

Для доказательства сходимости ряда Орем использует оценку

, (7.5)

где сумма второго ряда известна и равна 2. Эти результаты выходят за пределы античной математики и показывают, что сумма бесконечного ряда может быть как конечной, так и бесконечной. Имя Н. Орема присвоено одному из кратеров на обратной стороне Луны.

Нельзя не упомянуть и о ряде других, хотя и менее известных достижениях периода позднего Средневековья. Так в начале ХХ в. была найдена работа немецкого богослова, монаха Теодорика «О радуге», написанная в 1302 – 1310 г.г. В ней описаны опыты с разложением белого света на цветные лучи, а также рассмотрено и объяснено возникновение радуги, как первичной, так и вторичной, связанных с преломлением света на внешней и внутренней поверхностях капельного сфероида. Эта первая теория радуги неоднократно уточнялась и корректировалась последующими авторами и была завершена в 1637 г. Декартом.

XIII веком датируется известное «Письмо о магните», написанное на латыни в 1269 г. французским дворянином и энциклопедистом Пьером де Марикюром (Петр Перегрин). В нем автор описывает ряд остроумных экспериментов с магнитами и магнитными стрелками (которые уже были привезены в Европу из Китая), устанавливает их основные свойства и даже разрабатывает проект магнитного вечного двигателя! Также вводятся названия «северного» и «южного» полюсов магнита и констатируется их неразделимость. Фактически именно Марикюр придал магнитному полюсу его современный вид – стрелка на игле, окружённая кольцевой градусной шкалой.

Наконец, нельзя пройти мимо имени еще одного яркого минестреля, ученого и алхимика ХIII в. Раймонда Луллия (1235 – 1319), уроженца острова Майорка близ Испании. Выходец из обеспеченной семьи, он получил хорошее образование, будучи в молодости щеголем, дуэлянтом и любителем светских развлечений. Обладая литературным талантом, писал стихи и романы на каталонском языке, заметно подняв его культуру. Однако, достигнув 30-летнего возраста, уединяется, предается философским размышлениям и склоняется к богословию. Для совершенствования в теологических науках поступает в Парижский университет и получает степень доктора богословия. Убедив себя, что истинной верой является христианство, решил посвятить свою жизнь обращению неверных (мусульман, иудеев и др.) в истинную веру. С этой целью написал книгу «Великое искусство» (1307), в которой дал любопытное определение понятия Бога: « Бог есть бесконечная сумма бесконечных совершенств!» Для популяризации своих теологических идей и принципов, Луллий, проявив талант инженера, предложил схему своеобразного компьютера («буквенную мельницу»), образованного системой подвижных дисков, насаженных на общую ось. На их периферии наносились различные буквы и слова типа «вечность», «бог», «мудрость», «величественность» и др. Разработав систему правил поворачивания этих дисков, заключил, что путем комбинаций записанных букв и слов можно считывать с дисков фразы, выражающие Высшее Откровение (типа, «божественная мудрость бесконечна»). Аналогичным образом посредством этой «мельницы» можно преобразовывать тексты Корана в тексты Библии, что, по его мнению, должно было убедить мусульман принять христианство. Через 300 лет это устройство было усовершенствовано Лейбницем для разработки юридических текстов. К сожалению, миссионерская деятельность Луллия окончилась трагически – в возрасте 84 лет он в одной из поездок по Алжиру был побит камнями мусульманами и скончался по дороге домой на корабле спасшего его европейского купца.

Имя Луллия было известно и среди средневековых алхимиков. Еще обучаясь в Парижском университете, он заинтересовался алхимией и много времени уделял химическим опытам. До сих пор бытует легенда о том, что он изготовил для английского короля Эдуарда 25 тонн золотых монет высокой пробы из ртути, свинца и олова (в обмен на обещание короля организовать крестовый поход против сарацинов). Вряд ли можно поверить в эту легенду, однако в музеях Европы и сейчас можно увидеть золотые монеты, якобы изготовленные Раймондом Луллием!

Поражает плодовитость Луллия – им написано более 4000 работ, из которых около 500 посвящены алхимии. Среди них имеются широко известные «Завещание, излагающее в двух книгах всеобщее химическое искусство», «Опыты», «Сокращенное послание о камне», «Последнее завещание», «О тайнах природы». Уже при жизни он получил прозвище «Доктор Иллюминатиссимус» («Блестящий доктор»). Некоторые историки именно его считают изобретателем водки как пищевого продукта! О его жизни и делах ходило много легенд, последняя из которых гласит: спасший Луллия от рук мусульманских фанатиков генуэзский купец взял его на свой корабль и услышал от умирающего старика странное предсказание о том, что потомок купца откроет в будущем Новый Свет. Это пророчество сбылось через 173 года, так как купца звали Стефан Колумб!

Определенный интерес к науке проявляли не только теологи и дворяне, но и некоторые европейские монархи. Известно, что император Священной Римской империи Фридрих II Гогенштауфен (1195 – 1250) был страстным охотником, интересовался анатомией птиц и даже написал большой труд на эту тему. В нем он описал особенности скелета птиц, обсуждал механику их полета и привел много интересных данных об отличиях разных видов птиц. Там же он поместил специальное руководство по воспитанию ловчего сокола. Будучи высокообразованным человеком и владея 5 – 6 иностранными языками, он основал Неаполитанский университет. Там он открыл кафедру анатомии, на которой (впервые в Европе) разрешалось анатомировать трупы. Об интересе императора к «религиозной анатомии» говорит следующий его эксперимент: он приказал похоронить живьём одного провинившегося рыцаря, а затем разрыть могилу и проследить – вознесётся ли к небу душа покойника.

Он вел обширную переписку с некоторыми восточными правителями по вопросам астрономии, оптики, философии, а при своем дворе устраивал своеобразные «научные турниры», на которых ученые ставили друг другу различные задачи. Эти турниры стали прообразом будущих европейских «ученых диспутов». По его указанию были сделаны первые переводы на итальянский язык сочинений Аристотеля и Птолемея, а также были приняты законы, устанавливающие юридическое равенство прав простых граждан, дворян и священнослужителей. Не исключено, что принятие нового прогрессивного законодательства было произведено под влиянием уже знаменитой « Великой Хартии вольностей»(1215) английского короля И. Безземельного. К церковникам император он относился весьма скептически, вследствие чего католическая церковь не могла простить Фридриху его демократические вольности и, вероятно, как-то поспособствовала его внезапной смерти. Возможно так же, что это было связано с тем, что любимой книгой Фридриха было сочинение неизвестного автора «О трёх великих обманщиках: Моисее, Христе и Магомете». Некоторые историки объясняют подобный «политеизм» императора тем, что он вырос на Сицилии в городе Палермо, где в те времена происходило теснейшее соприкосновение двух миров – исламского и католического.

Резюме: Филопон и его антиаристотелизм, Герберт и система счисления, Фома Аквинский, Р.Бэкон, Р.Гроссетест, Л.Фибоначчи и начало европейской математики, И.Неморарий и «золотое правило» механики. Рождение понятий скорости и ускорения в оксфордской и парижской школах. Ж.Буридан, Н.Орем, У.Оккам. Европейская алхимия и Р.Луллий. Фридрих II и его новации.