Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
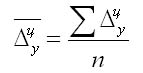
где n — число степенных абсолютных приростов в исследуемом периоде.
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
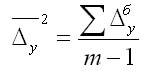
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период.
Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
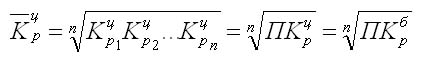
где n - число цепных коэффициентов роста; Кц - цепные коэффициенты роста; Кб - базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
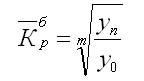
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
38. Основная тенденция развития.
Основной тенденцией развития (трендом) – называется главное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами:
Укрупнения интервалов (основан на укрупнении периодов времени, к которому относится наблюдение)
Скользящей средней (по исходным уровням ряда определяют расчетные уровни.)
Аналитического выравнивания (изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены усреднено с помощью математических функций. Путем теоретического анализа выявляется характер развития явления и на этой основе выбирается та или иная мат.функция: прямая, парабола второго порялка, показательная кривая…)
39. Сезонные колебания.
Сезонными называются периодические колебания, возникающие под влиянием смены времени года.
Большое значение сезонные колебания приобретают в изучении покупательского спроса населения на отдельные товары и виды услуг, а также на изменение цен и инфляцию.
Цель изучения сезонных колебаний – это прогнозирование и разработка оперативных мер по управлению их развитием во времени.
Сезонные колебания характеризуются индексами сезонности. Для выявления сезонных колебаний обычно берут данные за ряд лет, чтобы выявить устойчивую сезонную волну.
Если ряд динамики содержит определенную тенденцию в развитии явления, то сначала осуществляют аналитическое выравнивание ряда, затем сравнивают фактические теоретические уровни. Индекс сезонности в этом случае равен
|
где n – число лет, за которые даны уровни; уф – фактические данные; Уt – теоретические данные.
|
Расчет сезонных колебаний можно выполнять другим методом в зависимости от характера динамики.
Если годовой уровень явления из года в год остается относительно неизменным, то индексы сезонности исчисляются по формуле
.
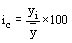Для сопоставления величины сезонных колебаний по нескольким предприятиям или периодам может быть использовано среднее квадратическое отклонение, исчисляемое по формуле
|
где n – число месяцев; Jсез. – индекс для каждого месяца.
|
Чем меньше среднее квадратическое отклонение, тем меньше величина сезонных колебаний.