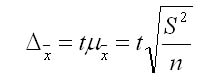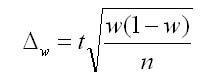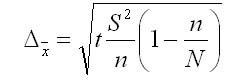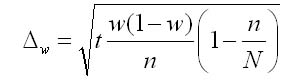28. Ошибка выборки.

Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

В собственнослучайном отборе заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Разности   —   и W — р называются ошибкой выборки, которая делится на ошибку регистрации и ошибку репрезентативности. Первая часть ошибки выборки возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая часть ошибки возникает из-за постоянного или спонтанного несоблюдения принципа случайности отбора. Ее трудно обнаружить и устранить, она гораздо больше первой и потому ей уделяется основное внимание.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака: ех = \х – х\;

2) для доли (альтернативного признака): ew = \х – p\.

Только выборочным наблюдениям присуща ошибка выборки.

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Средняя ошибка выборки зависит от степени варьирования изучаемого признака.

Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки.

Предельная ошибка - максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.

1. Предельную ошибку выборки для средней при повторном отборе рассчитывают по формуле:

	где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;мю х — средняя ошибка выборки.
2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:
3. Предельная ошибка выборки для средней при бесповторном отборе:
4. Предельная ошибка выборки для доли при бесповторном отборе: