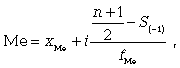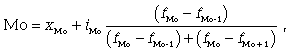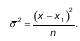23. Структурные средние.

1. Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.

Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина.

Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10): 2= 8,5.

Т.е. для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле:

n - число единиц в совокупности

Численное значение медианы обычно определяют по формуле

где xМе - нижняя граница медианного интервала; i - величина интервала; S-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала.

Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.

Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.

Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.

2. Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.

где xМо - нижняя граница модального интервала; iМо - величина модального интервала;

fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.

24. Понятие вариации.

Вариация — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений. Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками.

Различают вариацию признака: случайную и систематическую.

Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.

Для характеристики колебания признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (Х_мах) и наименьшим (x_mjn) значениями вариантов:

Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений.

Меру вариации более объективно отражает показатель дисперсии