Билет №7

Первое начало термодинамики представляет собой обобщенный закон сохранения энергии. Для его формулировки необходимо определить три величины: внутреннюю энергию U, работу А и теплоту Q.

Внутренняя энергия. Внутренней энергией U макросистемы называют величину, включающую

1 суммарную кинетическую энергию хаотического движения всех молекул;

2 потенциальную энергию взаимодействия всех молекул макросистемы;

3 внутреннюю энергию самих молекул, атомов, ядер и т.д…

В случае модели идеального газа виды энергии, перечисленные в пунктах 2 и 3, не включаются во внутреннюю энергию по условиям самой модели. Внутренняя энергия является функцией состояния, т.е. величина ее изменения не зависит от того, каким путем макросистема перешла из одного состояния в другое. Кроме того, внутренняя энергия аддитивна, т.е. внутренняя энергия системы равна сумме внутренних энергий составляющих систему частей.

Работа и количество теплоты. Внутреннюю энергию можно изменить двумя способами: или при совершении системой работы А над внешними телами, или путем теплопередачи. В первом случае система совершает механическую работу над внешними телами, во втором происходит непосредственный обмен энергией при столкновениях молекул системы с молекулами внешней среды, который не сопровождается перемещением внешних тел. Близким по результату является и передача тепла путем излучения.

Первое начало термодинамики утверждает, что полученное макросистемой количество теплоты Q идет на приращение внутренней энергии ΔU и совершение системой работы над внешними телами:

. (6)

Первое начало термодинамики в дифференциальной форме следует писать в виде

, (7)

потому, что малые приращения и не являются полными дифференциалами, так как зависят от вида процесса, связывающего последовательные состояния системы. На практике, где вид процесса известен, это не создает особых проблем, так как при известном процессе указанные приращения в математическом отношении ничем не будут отличаться от полных дифференциалов.

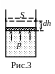Работа, совершаемая термодинамической системой. Пусть газ находится в цилиндре под поршнем сечения S под давлением р (рис.3). Если объем газа увеличивается на под действием нормальной силы , значит, что газ совершил работу . Дифференциально малая работа газа равна произведению давления и приращения объема:

. (8)

И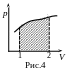 сключительно полезно запомнить, что если объем не меняется,  газ работу не совершает. Чтобы вычислить работу газа в конкретном процессе, необходимо знать вид зависимости р( ), чтобы проинтегрировать:

. (9)

Р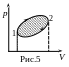 абота зависит от пути (вида процесса, т.е. зависимости р( )), что видно из графика на рис.4, поскольку физический смысл интеграла в формуле (9) есть площадь под кривой р( ) в указанных пределах. Если кривая р( ) – замкнутая (рис.5), то система возвратилась в исходное состояние. Тогда принято говорить, что система совершила круговой цикл. Поскольку работа на участке 1-2 равна площади под верхней частью кривой, а на участке 2-1 работа равна площади под нижней частью кривой (причем эта работа отрицательна, т.к. изменен порядок пределов интегрирования), то алгебраическая сумма этих работ, т.е. работа за цикл равна только заштрихованной площади. Следовательно, работа при любом круговом процессе равна площади замкнутой кривой в координатах р- . Запишем с учетом (8) I начало термодинамики сразу в виде

. (10)

Теплоемкость идеального газа. Теплоемкостью тела называется количество теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1 кельвин (К):

. (11)

Поскольку dQ не является полным дифференциалом, теплоемкость тела также является функцией процесса и к тому же зависит от количества вещества (массы тела). Поэтому используют молярную теплоемкость C (количество теплоты, необходимое для нагревания 1 моля вещества на 1 К) или удельную теплоемкость с (количество теплоты, необходимое для нагревания 1 кг вещества на 1 К). Очевидно, для нахождения С необходимо разделить на число молей вещества, а для нахождения с необходимо разделить на массу тела. Отсюда размерности: [С] =Дж/мольК , [c] =Дж/кгК , и связь между удельной и молярной теплоемкостями: С=Мс.

Молярной теплоемкостью при постоянном объеме называется частная производная:

. (12)

Учитывая, что , из (12) следует, что U_=C_VT,  . Молярной теплоемкостью при постоянном давлении (изобарный процесс) называется частная производная:

. (13)

Разделим I-е начало термодинамики для 1 моля вещества ( ) на dT:

,  . (14)

В изобарном процессе (р=const) слева стоит С_р. Из уравнения состояния для 1 моля вещества (pV_=RT) найдем и подставим в (14 ) вместо последнего слагаемого:

. (15)

Отсюда виден смысл постоянной R: это работа расширения 1 моля газа в изобарном процессе при изменении температуры на 1 К.