18. Предел функций в точке. Арифметические операций над пределами.
1. Функция одной переменной. Определение предела функции в точке по Коши. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа существует такое положительное число , что при всех х ≠ а, таких, что |x – a | < , выполняется неравенство | f(x) – a | < .
Указанный предел обозначается так:
Критерий Коши существования предела функции в точке. Число b – предел функции у = f(x) при х, стремящемся к а, тогда и только тогда, когда для любого числа > 0 можно указать такую проколотую d-окрестность точки а, что для любых чисел х1 и х2, содержащихся в этой окрестности, выполняется неравенство | f(x1) – f(x2) | < .
Пусть 
Тогда
существуют пределы суммы и произведения
функций f(x)
и g(x),
а в случае с ≠ 0 – и частного этих функций,
причём:
Если
определена сложная
функция F(f(x)),
причём
то
существует и предел сложной функции,
причём
В теории пределов доказываются следующие два утверждения.
Первый
замечательный предел: 
Второй
замечательный предел: 
где е –
знаменитое иррациональное число, e=
2,71...
При вычислении пределов для раскрытия неопределённостей, связанных с дифференцируемыми функциями, часто используют правило Лопиталя.
2. Функция многих переменных. Пусть функция у = f(x1; x2; …; xn) определена в некоторой выколотой окрестности точки Р(р1; р2; …; рn), принадлежащей области n–мерного пространства, состоящей из точек Х(x1; x2; …; xn). Число b называется пределом функции у =f(x1; x2; …; xn) при Х, стремящейся к Р, если для любого числа > 0 существует такое положительное число , что в точках Х выколотой окрестности точки Р, задаваемой неравенствами
выполняется неравенство | f(x1;x2; ...;xn) – b | < .
арифметические операции над пределами Если limx af(x) = A,limx ag(x) = B, то
limx a[f(x) g(x)]=A B,
limx af(x)g(x) = AB
limx af(x)/g(x) = A/B, B 0
Эта теорема непосредственно следует из соответствующей теоремы о пределах последовательностей.
19. Два замечательных предела и их следствия.
.
Лемма. Если
и 
,
то 
.
Рассмотрим
в координатной плоскости круг единичного
радиуса с центром в точке О. Пусть 
AOB
= x, где 
.
Пусть С – проекция точки В на ось Ох, D
– точка пересечения луча ОВ и прямой,
перпендикулярной Ох, проходящей через
т. А. Тогда BC = sin(x), DA = tg(x). Пусть также 
-
площади треугольника AOB, сектора AOB,
треугольника AOD соответственно.
Тогда 
, 
, 
.
Так как 
,
то 
.
Если 
,
то sin(x)>0 и выполняется неравенство 
.
Так как функции 
и
cos(x) четные, то данное равенство верно
и при 
,
ч.т.д.
Воспользуемся
данной леммой. В силу непрерывности
косинуса
.
Переходя в соотношении
к
пределу при
получаем
равенство
.
=
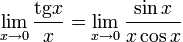=1*1=1
=
=
=1
=
=
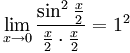=1
=
=
=1
Рассмотрим случай, когда
.
Известно, что последовательность
при 
.
Обозначим 
и 
.
Так как 
и 
,
то 
.
Из этого, пользуясь определением
предела:
.
Пусть x – произвольное вещественное
число такое, что 
и
n = [x]. Тогда 
или
, 
.
В силу монотонности показательной и
степенной функции, получаем: 
<
.
Из этого следует
,
т.е. по определению предела это означает,
что теорема справедлива в случае,
когда
.
Докажем,
что 
.
Положим x=-1–t. Тогда 
при 
и
=
откуда
следует, что теорема доказана, так
как 
при
и 
.
=
=1*1=1
= = =1
= = =1
= = =1