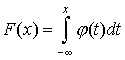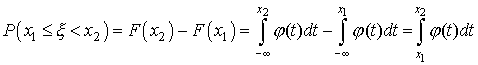Дискретные и непрерывные случайные величины

Вернемся к примерам, приведенным выше. В первом из них случайная величина   могла принять одно из следующих возможных значений: 0,1,2,…,100.

Эти значения отделены одно от другого промежутками, в которых нет возможных значений  . Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. Во втором примере случайная величина могла принять любое из значений промежутка  . Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.

Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.

 

  

 

Числовые характеристики дискретных случайных величин

Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: , где   – возможные значения случайной величины  , а   – соответствующие вероятности. Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу: 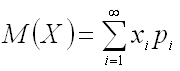, причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

 

  

 

Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной: . 2. Постоянный множитель можно вынести за знак математического ожидания: . 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: . Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий. 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: . Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

Пусть производится   независимых испытаний, в каждом из которых вероятность появления события   постоянна и равна  . Тогда справедлива следующая теорема. Теорема. Математическое ожидание числа появлений события   в   независимых испытаниях равно произведению числа испытаний на вероятность появления этого события в каждом испытании: .

Разность между случайной величиной и ее математическим ожиданием называется отклонением. Теорема. Математическое ожидание отклонения равно нулю: . Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величиной от ее математического ожидания: . Дисперсия имеет размерность, равную квадрату размерности случайной величины. Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины   и квадратом ее математического ожидания: .

 

  

 

Свойства дисперсии

1. Дисперсия постоянной величины равно нулю: . 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: . 3. Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих случайных величин: . Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин. 4. Дисперсия разности двух независимых случайных величин равно сумме дисперсий этих случайных величин: .

Теорема. Дисперсия числа появлений события   в   независимых испытаниях, в каждом из которых вероятность   появления события постоянна, равна произведению числа испытаний на вероятность   появления и вероятность   непоявления этого события в одном испытании: .

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: . Размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины.

54) Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.

При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности (   ):

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n  с  вероятностями, вычисляемыми по формуле Бернулли:

xi	0	1	…	m	…	n
pi	qn		…		…	pn

где q=1-p; 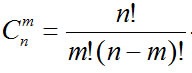   - число сочетаний из n элементов по m.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна  .

55) Функцией распределения вероятностей называют функцию  , определяющую вероятность того, что случайная величина   в результате испытания примет значение, меньшее  , то есть: . Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

 Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:   

   Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.     Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.     Случайная величина   называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция*  , удовлетворяющая для любых значений x равенству

(22)

   Функция   называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁<x₂, то на основании формул (20) и (22) имеем

(23)

   Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств   равна площади криволинейной трапеции с основанием [x₁,x₂], ограниченной сверху кривой 

56) В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.

Пусть требуется измерить некоторую величину  . Результаты измерений

естественно рассматривать как значения случайных величин  , полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить  . Следовательно, возникает задача оценить параметр . Для решения задачи рассмотрим случайную величину

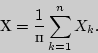
Тогда 

Это обстоятельство приводит к мысли построить статистические характеристики:

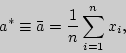
Первая представляет среднее арифметическое наблюденных значений случайной величины   и статистическую дисперсию - во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины   и к дисперсии

При ограниченности наблюдений эксперимента заменой   и   на   и   совершаем погрешность, а при небольшом числе наблюдений величины   ,   являются случайными величинами. Возникает задача об оценке неизвестных параметров  ,   случайной величины   на основе экспериментальных данных, т.е. задача - найти подходящие значения этих параметров.

Множество результатов измерений   величины   называется выборкой объема  . Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину   рассматривать как случайную величину, функцию распределения которой

следует определить.

Полученный статистический материал  ,  , ...  наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д.

Если выборка объема   содержит   различных элементов  , причем   встречается   раз, то число   называется частотой элемента  , а отношение   называется относительной частотой элемента  . Очевидно, что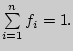 

Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы  ', а вторая - их частоты   (относительные частоты  .

Гистогра́мма (от др.-греч. ἱστός — столб + γράμμα — черта, буква, написание) — способ графического представления табличных данных.

Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.

57) ♦ Измерение — это совокупность операций по применению техни­ческого средства, хранящего единицу физической величины, обес­печивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения данной величины. ♦

 

Результат измерения представляет собой конечный продукт некоего производственного процесса, имеющего, как и любая другая продукция, свои показатели качества. Среди них важней­шим с учетом того, что речь идет об измерительном процессе, показателем качества является точность полученного результата.

Под точностью результата измерений понимают одну из его характеристик, отражающую близость к нулю погрешности.

Погрешность результата измерения — это отклонение резуль­тата измерения от истинного значения измеряемой величины. Так как истинное значение может быть получено только в ре­зультате бесконечного процесса измерений и требует непрерыв­ного совершенствования методов и средств измерений, то оно всегда остается неизвестным. В практических целях вместо ис-тинного значения используется действительное значение изме­ряемой величины, т.е. значение, полученное экспериментальным путем и настолько близкое к истинному, что в рамках постав­ленной измерительной задачи может быть использовано вместо него. Таким образом, погрешность измерения может быть вы­ражена зависимостью:

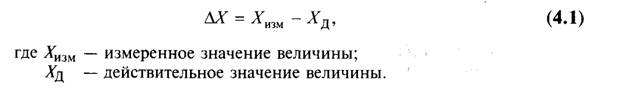
Значение АХ получило название абсолютной погрешности измерения. Абсолютная погрешность измерения выражена в единицах измеряемой величины. К сожалению, судить по зна­чению абсолютной погрешности о качестве измерения нельзя. Действительно, если известно, что погрешность измерения со­ставляет ± 1 мм, то оценить его качество затруднительно. Не­обходимо сопоставить значение абсолютной погрешности и значение измеренной величины. Эта задача решается введением понятия относительной погрешности измерения. Относительная погрешность измерения рассчитывается как отношение абсо­лютной погрешности к действительному (или измеренному) значению величины. Относительную погрешность выражают в долях единицы или в процентах в соответствии с зависимостью:

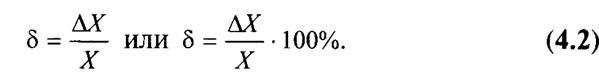
По закономернорти появления погрешности делятся на сис­тематические и случайные. При этом, как правило, самостоя­тельного значения они не имеют, а рассматриваются в качестве составляющих собственно погрешности измерения.

 

♦  Систематической погрешностью измерения называется состав­ляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. ♦

 

Рекомендациями МИ 1317—04 «ГСИ. Результаты и характе­ристики погрешности измерений. Формы представления. Спо­собы использования при испытаниях образцов и контроле их параметров» установлено, что в качестве характеристик система­тической погрешности измерения целесообразно использовать среднее квадратическое отклонение неисключенной системати­ческой составляющей или границы, в которых неисключенная систематическая составляющая находится с заданной вероятно­стью (в том числе и с вероятностью, равной единице). Первая характеристика получила название точечной; вторая — интер­вальной. При проведении измерений принято вводить поправки в результаты и исключать систематическую составляющую. Од­нако всегда остаются погрешности вычисления и погрешности в определении значения самих поправок, а также систематические составляющие, ввести поправки на величину которых не пред­ставляется возможным ввиду их малости. Поэтому считается, что результат всегда содержит систематическую составляющую погрешности измерения, которую называют неисключенной.

 

♦ Случайной погрешностью измерения называется составляющая погрешности, изменяющаяся случайным образом (по знаку и зна­чению) при повторных измерениях одной и той же физической ве­личины, проведенных с одинаковой тщательностью. ♦

 

В качестве характеристик случайной составляющей погреш­ности используются ее среднее квадратическое отклонение и (при необходимости) нормализованная автокорреляционная функция.

Для характеристики погрешности измерений кроме характе­ристик случайной и систематической составляющих используют­ся среднее квадратическое отклонение и границы, в пределах ко­торых погрешность измерений находится с заданной вероятно­стью. Точечные характеристики рекомендуется использовать в случаях, когда результаты измерений (испытаний) используются совместно с другими результатами измерений, а также при расче­тах погрешностей величин, функционально связанных с результа­тами измерений (например, результатов косвенных измерений). Интервальные характеристики используются для решения опре­деленных технических задач. Если интервал ограничен наиболь­шим и наименьшим значениями погрешности измерений, а ис­тинное значение погрешности находится внутри него с заданной вероятностью, то этот интервал называется доверительным интер­валом, а вероятность — доверительной вероятностью.

В связи с тем, что истинное значение и измеряемой величи­ны, и погрешности результата измерения неизвестны, а измере­ниям подвергаются все больше величин, для которых само оп­ределение «физическая величина» неприменимо,  в последнее

время для оценки качества измерительной информации все ча­ще используется понятие «неопределенность измерений».

 

•  Неопределенность измерений — параметр, связанный с резуль­татом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине. ♦

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Доверительная вероятность показывает, с какой вероятностью ответ попадет в границы доверительного интервала. Для простоты можно понимать её как точность выборки. Как правило, используется 95% (для стандартных исследований) или 99% (для более точных исследований).

Доверительный интервал можно понимать как погрешность. Задает ширину диапазона по обе стороны от выбранной точки, куда могут попадать ответы. Общепринятой в управленческой практике шириной доверительного интервала считается +/-5,0% (для стандартных исследований) или +/-2,5% (для более точных исследований).

58) В прямых измерениях физическая величина измеряется

непосредственно (например, измерение длины предмета линейкой,

штангенциркулем или микрометром, силы тока – амперметром и т.д.).

При косвенных измерениях искомая величина не измеряется, а

вычисляется по результатам измерений других величин (например, измеряя

силу тока и напряжение на зажимах электроплитки, можно вычислить ее

тепловую мощность и сопротивление).

В физическом эксперименте любое измерение (прямое или косвенное) дает

лишь приблизительное значение данной физической величины. Физика – наука

естественная, а абсолютная точность присуща лишь математике.

Действительно, при измерении длины полученный результат будет

зависеть, по крайней мере: 1) от точности выбранного нами прибора

(штангенциркуль, например, позволяет измерять с точностью до 0,1 мм, а

линейка до 1 мм); 2) от внешних условий: температуры, деформации, влажности

и т.д.

Разумеется, результаты косвенных измерений, вычисленные по

приближенным результатам, полученным в прямых измерениях, также будут

приближенными. Поэтому вместе с результатом всегда необходимо указывать

его точность, называемую абсолютной погрешностью результата Δ.

Пример: L = (427,1 ± 0,2) мм

1