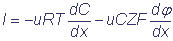46. Реограф.

 

     Реограф -электронное устройство, предназначенное для преобразования колебаний  импеданса живой ткани или его составляющих, обусловленных пульсовыми изменениями кровенаполнения в пропорциональный электрический сигнал.

     Принцип работы реографа заключается в следующем: от генератора высокой  частоты реографа с помощью электродов через иссле

дуемый орган пропускается ток высокой частоты.  При этом на исследуемом участке (органе) возникает падение напряжения.  Изменения кровенаполнения в исследуемом органе приводят  к  изменениям его импеданса и пропорциональным изменениям амплитуды высокочастотного напряжения.  После усиления с помощью детектора и  фильтров выделяется низкочастотная составляющая,  представляющая собой реографический сигнал (реограмму) - рисунок.

 

Используется переменный ток с частотами 30-300 кГц, величина тока составляет 1-5 мА.  Реоплетизмограф РПГ-202 -   = 40  кГц,

I = 2 мА.

     Реоэнцефалография - метод исследования мозгового кровообращения, основанный на измерении и записи пульсовых колебаний полного электрического сопротивления  (импеданса)  головного  мозга при пропускании через него тока высокой частоты, слабого по силе и напряжению.

     Реоэнцефалограф - прибор, предназначенный для этих целей.

47. Теорема Пригожина, ее биофизический смысл.

Теорема Пригожина — теорема термодинамики неравновесных процессов. Согласно этой теореме, стационарному состоянию системы (в условиях, препятствующих достижению равновесного состояния) соответствует минимальное производство энтропии. Если таких препятствий нет, то производство энтропии достигает своего абсолютного минимума — нуля. Доказана И. Р. Пригожиным в 1947 из соотношений взаимности  Онсагера. Теорема Пригожина справедлива, если кинетические коэффициенты в соотношениях Онсагера постоянны; для реальных систем она справедлива лишь приближённо, поэтому минимальность производства энтропии для стационарного состояния не является столь общим принципом, как максимальность энтропии для равновесного состояния.

Формулировка теоремы: В стационарном состоянии продукция энтропии внутри термодинамической системы при неизменных внешних параметрах является минимальной и константной. Если система не находится в стационарном состоянии, то она будет изменяться до тех пор, пока скорость продукции энтропии, или, иначе, диссипативная функция системы не примет наименьшего значения.

48. Уравнение Нернста-Планка для мембраны уравнение нернста-планка

Уравнение Нернста-Планка описывает процесс пассивного транспорта ионов в поле электрохимического потенциала. Поток I заряженных ионов пропорционален градиенту электрохимического потенциала в направлении оси x и зависит от подвижности u и концентрации C ионов:

, где

F - число Фарадея,

Z - валентность иона,

T - абсолютная температура,

R - газовая постоянная,

ϕ - электрический потенциал на мембране.

49. Виды событий. Вероятность событий

Событием называется всякий факт, который может произойти или не произойти в результате опыта.

Виды событий:  1) События называются несовместными, если появление одного из них исключает появление других. Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).

2) Полной группой событий называется совокупность всех возможных результатов опыта.

3)  Достоверным событием называется событие, которое наверняка произойдет в результате опыта. 

4) Событие называется невозможным, если оно никогда не произойдет в результате опыта.

Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.

5) События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

Вероятность события количественно характеризует возможность (шанс) осуществления этого события в ходе случайного эксперимента. В данном параграфе мы начинаем изучать возможности, предоставляемые теорией вероятности для сравнительного анализа ситуаций, возникающих при различных комбинациях равновероятных событий.

Представим, что у нас проводится эксперимент с пространством из n элементарных исходов, которые равновероятны. Элементарные исходы являются несовместными событиями (напомним, что несовместные события - это те, которые не могут произойти одновременно), поэтому вероятность каждого из них равна 1/n. Допустим, нас интересует событие А, которое наступает только при реализацииблагоприятных элементарных исходов, количество последних m (m< n). Тогда, согласно классическому определению, вероятность такого события:

Р(А)=m/n.

Для любого события А справедливо неравенство: 0 < P(A) <1.n>

Пример 1. Лотерея состоит из 1000 билетов, среди них 200 выигрышных. Наугад вынимается один билет из 1000. Чему равна вероятность того, что этот билет выигрышный? Решение: различных исходов в этом примере 1000 (n=1000). В интересующее нас событие А входят 200 исходов (m=200). Таким образом,

50. Для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных.

Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей. Этих теорем две:

• теорема сложения вероятностей;

• теорема умножения вероятностей.

Теорема сложения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В) (1)

Теорема умножения вероятностей

Введем понятие независимые и зависимые события.

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р (А/В)

Пример:

В урне два белых и один черный. Два лица вынимают из урны по одному шару. Рассматриваются события: А- появление белого шара у 1-го лица; В – появление белого шара у 2-го лица.

Решение: Р(А) до того как произошло событие В равно 2/3. Если событие В произошло, то Р(А)=1/2. Таким образом, событие А зависит от события В.

Условие независимости события А от события В можно записать в виде:

Р(А/В) = P(A) (10)

а, условие зависимости: Р(А/В) ≠ P(A) (11)

50)Теорема сложения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В) (1)

Теорема сложения вероятностей применима к любому числу несовместных событий. В общем виде ее удобно записать:

Р(∑Ai) = ∑Р(Ai) (2)

Отметим следствия вытекающие из теоремы сложения вероятностей.

Следствие 1: Если события А1, А2, …, Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

∑Р(Ai) = 1 (3)

Перед тем как вывести второе следствие теоремы сложения, введем понятие «противоположные события».

Противоположными событиями называются два несовместных события, образующих полную группу. Событие противоположное событию А принято обозначать A.

Пример:

Событие А – безотказная работа всех элементов технической системы; A – отказ хотя бы одного элемента.

Следствие 2: Сумма вероятностей противоположных событий равна единице:

P(A) + P(A) =1 (4)

Следствие 2 есть частный случай следствия 1.

Вероятность суммы двух совместных событий выражается формулой:

Р(А+В) = Р(А) + Р(В) – P(AB) (5)

Аналогично вероятность суммы трех совместных событий вычисляется по формуле:

Р(А+В+С) = Р(А) + Р(В) + Р(С) – P(AB) – P(AС) – P(ВС) + Р(АВС) (6)

Общая формула для вероятности суммы любого числа совместных событий:

Р(∑Ai) = ∑Р(Ai) – ∑Р(AiAj) + ∑Р(AiAjAk) – (-1)n-1P(A1A2…An) (7)

где суммы распространяются на различные значения индексов i; i, j; i, j, k и т.д.

Из формул (5) и (6) можно записать аналогичную формулу для произведения событий

P(AB) = Р(А) + Р(В) – Р(А+В) (8)

Р(АВС) = Р(А) + Р(В) + Р(С) – P(A+B) – P(A+С) – P(В+С) + Р(А+В+С) (9)

Теорема умножения вероятностей

Введем понятие независимые и зависимые события.

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р (А/В)

Пример:

В урне два белых и один черный. Два лица вынимают из урны по одному шару. Рассматриваются события: А- появление белого шара у 1-го лица; В – появление белого шара у 2-го лица.

Решение: Р(А) до того как произошло событие В равно 2/3. Если событие В произошло, то Р(А)=1/2. Таким образом, событие А зависит от события В.

Условие независимости события А от события В можно записать в виде:

Р(А/В) = P(A) (10)

а, условие зависимости: Р(А/В) ≠ P(A) (11)

Теорема умножения: Вероятность произведения двух событий равна произведению вероятности

Р(АВ) = P(A)×Р(В/А) (12)

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

Р(А1А2…Аn ) = P(A1)×Р(А2/А1)×Р(А3/А1А2)×…×Р(Аn/А1А2…А n-1) (13)

Следствие1: Если событие А не зависит от события В, то и событие В не зависит от события А

Следствие2: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий

P(AВ) = P(А)×Р(В) (14)

Р(А1А2…Аn ) = P(A1)×Р(А2)×….×Р(Аn) (15)

Формула полной вероятности

Следствием основных теорем является так называемая формула полной вероятности.

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий:

Н1, Н2, ….Нn,

Образующих полную группу несовместных событий. Будем эти события называть гипотезами.

В этом случае, вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе

Р(А)=∑Р(Hi)×P(A/Hi) (16)

Теорема гипотез (формула Бейеса)

Имеется полная группа несовместных гипотез Н1, Н2, …., Нn. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н1), Р(Н2)…. Р(Нn).

Произведен опыт, в результате которого наблюдалось появление некоторого события А. Как следует изменить вероятность гипотез в связи с появлением этого события? По существу речь идет о том, чтобы найти условную вероятность Р(Нi/А) для каждой гипотезы.

Р(Нi/А) = [Р(Нi)×Р(Нi/A] / [∑Р(Hi)×P(A/Hi)], i = 1, 2, …, n (17)51)Классическое определение вероятности 

(m - число благоприятных исходов опыта; n - число всех его исходов)

     Теорема сложения вероятностей несовместных событий 

     Теорема сложения вероятностей совместных событий 

     Теорема умножения вероятностей независимых событий 

     Теорема умножения вероятностей зависимых событий 

где   - вероятность события B при условии, что произошло событие A.

     Формула полной вероятности 

где   - полная группа гипотез, т. е.

(  - достоверное событие).

52)

В ходе исследований предложены и изучены: диагностика методом наибольшего правдоподобия, алгоритм, повышающий скорость и надежность определения вероятности болезни методом наибольшего правдоподобия; критерий эффективности диагностики, проведенной расчетными методами; использование многомерных распределений при диагностике; имитационные модели болезней для решения методических проблем диагностики и тестирования разрабатываемых методов.

Содержание изложено на 169 страницах, включает 33 рисунка и 29 таблиц, список использованной литературы из 144 публикаций.

53) Уже в первой части приводились события, состоящие в появлении того или иного числа. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример 5.1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, ..., 100.

Пример 5.2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т.д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку  .

Будем далее обозначать случайные величины прописными буквами  , а их возможные значения — соответствующими строчными буквами  . Например, если случайная величина   имеет три возможных значения, то они будут обозначены так:  .