23.3. Цифровые корректирующие устройства

Цифровые корректирующие устройства реализуются в виде ал­горитмов в программах на ЭВМ или в виде цифровых блоков, модели-рующргх законы коррекции. Следует отметить, что перед разработкой алгоритмов реализации цифровых корректирующих устройств необ­ходимо проверить передаточную функцию регулятора на отсутствие нулей и полюсов, превышающих по модулю единицу. Ряд типовых, наиболее часто применяющихся цифровых корректирующих фильт­ров, представлено ниже.

Интегрирующее звено первого порядка

Дифференцирующее звено первого порядка

Апериодическое звено с постоянной времени Т_а

Интегро-дифференцирующее звено первого порядка

где

В общем виде передаточная функция цифрового корректирую­щего устройства имеет вид

Соответствующая структурная схема цифрового корректирующе­го устройства представлена на рис. 23.3.

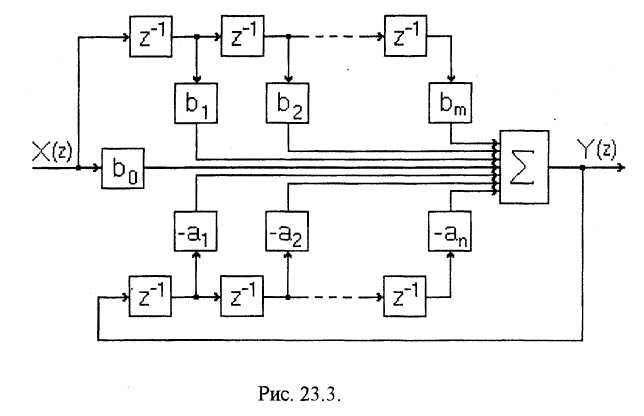
Используя выражение (23.7) можно составить цифровые фильт­ры П, ПИ, ПД и ПИД-типа. С целью повышения помехозащищеннос­ти алгоритмов, использующих операцию дифференцирования, вводят ограничение на функцию дифференцирования за счет добавления апе­риодического звена, используют алгоритмы сглаживания и усредне­ния сигнала ошибки или первой его разности. Эффективным средством повышения помехоустойчивости является исключение сигнала ошиб­ки из дифференцирующей части и применение вместо него сигнала обратной связи. Соответствующая структурная схема системы представлена на рис. 23.4.

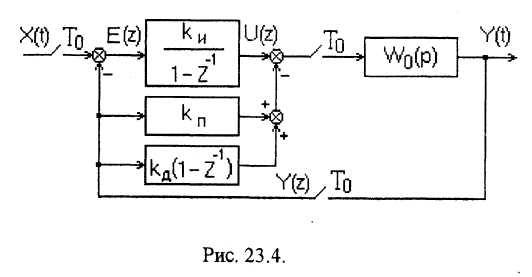
На рисунке:

W_o(p) - передаточная функция системы, охваченная данной об­ратной связью.

Алгоритм регулятора имеет вид

где k_п, k_и, k_д - коэффициенты передачи пропорциональной, интегральной и дифференциальной составляющих сигнала ошибки регулирования.

Ряд передаточных функций и временных характеристик особых (интерполирующих) линейных цифровых корректирующих устройств представлен в [40].

23.4. Параллельные корректирующие устройства

Возможность коррекции систем автоматического регулирования с помощью параллельных корректирующих устройств, с приведением структурных схем и построением логарифмических частотных харак­теристик, хорошо обоснована в [120, 132]. Показано, что с помощью параллельных корректирующих устройств можно повысить показате­ли качества системы в той же степени, как с последовательными кор­ректирующими устройствами.

Параллельные корректирующие устройства используются для введения в закон управления интегралов и производных. Для повыше­ния порядка астатизма служат изодромные устройства, представляю­щие собой интегрирующее звено, включенное параллельно основно­му каналу управления, рис. 23.5.

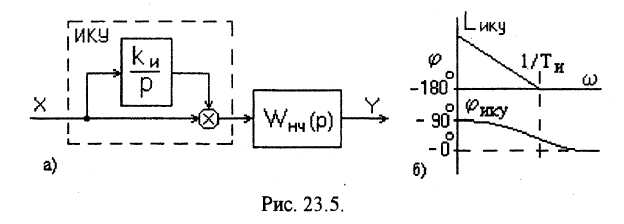
На рисунке: ИКУ - изодромное корректирующее устройство; W_HЧ(p) - передаточная функция неизменяемой части системы.

Передаточная функция изодромного устройства имеет вид

где Т_и = 1/k_и - постоянная времени изодромного устройства.

Логарифмические частотные характеристики (рис. 23.5, б) показы­вают, что воздействие на амплитуду и фазу сигнала наблюдается только в области низких частот до . Это позволяет, при соответствующем выборе значения , повысить порядок астатизма системы без изменения характера ЛАЧФ и ЛЧФХ в среднечастотной области (зоне ). Для вве­дения в закон управления нескольких интегралов возможно последова­тельное включение нескольких изодромных звеньев.

Структурная схема введения в канал управления производной входного сигнала представлена на рис. 23.6.

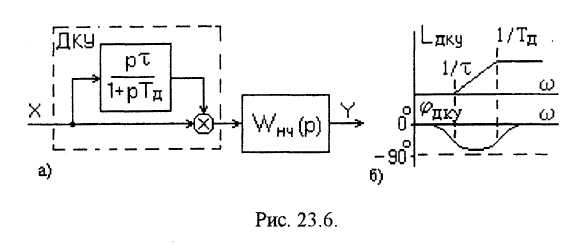
На рисунке:

ДКУ - дифференцирующее корректирующее устройство;

T_д- постоянная времени дифференцирующего звена;

- время задержки.

На этом же рисунке приведены логарифмические частотные ха­рактеристики ДКУ

Параллельные корректирующие звенья в сочетании с последова­тельными корректирующими устройствами позволяют создавать сис­темы комбинированного управления. Комбинированные системы уп­равления позволяют оптимизировать замкнутый контур регулирования с учетом требований к устойчивости системы и качеству отработки внешних возмущений.

Гибкая обратная связь подает на вход охваченного ею звена (или нескольких звеньев) величину пропорциональную первой производ­ной от выходной величины этого звена. В более общем случае, кроме первой производной, можно подать вторую и более высокие производ­ные выходной величины.

Повышение порядка астатизма системы. Повышение порядка астатизма системы обеспечивает увеличение динамической точности отработки сигнала. Существующие многочисленные схемы являются модификациями двух основных методов.

Метод В.А. Боднера заключается в введении в основную цепь управления дополнительных интегрирующих звеньев, охваченных прямой параллельной жесткой связью, рис. 23.7.

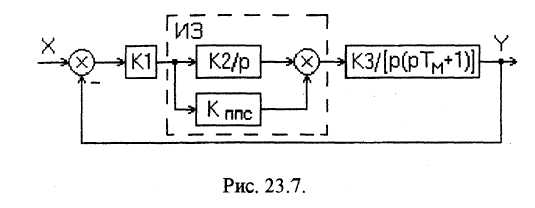
На рисунке:

ИЗ - дополнительное интегрирующее звено,

К_ппс - передаточный коэффициент звена прямой параллельной жесткой связи.

Эквивалентная передаточная функция дополнительного интегри­рующего звена

Где - постоянная времени.

Из (23.10) очевидно, что передаточная функция дополнительно­го звена дает эффект аналогичный включению последовательного кор­ректирующего ПИ-регулятора. Постоянную времени можно менять выбором желаемого значения .

Метод М.В. Меерова заключается в введении в основную цепь операционного усилителя К2 с очень большим коэффициентом усиле­ния, охваченного корректирующей отрицательной обратной связью с рис. 23.8

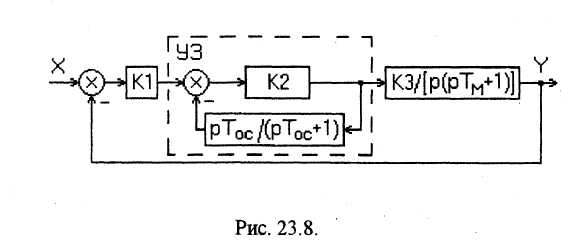
На рисунке:

УЗ - усилительное звено с корректирующей обратной связью.

На этом принципе построены ПИ-регуляторы.

Комбинированные системы коррекции. Системы, в которых од­новременно с регулированием по отклонению регулируемой величи­ны осуществляется регулирование по возмущению, называются сис­темами комбинированного регулирования. Системы комбинированно­го регулирования позволяют синтезировать инвариантные системы, в которых параллельно естественному пути прохождения возмущающе­го воздействия на объект создано компенсирующее воздействие, ока­зывающее на регулируемый параметр такой же эффект по величине, как и возмущающее воздействие, но противоположное по знаку. Ти­пичная схема комбинированной системы автоматического регулиро­вания представлена на рис. 23.9.

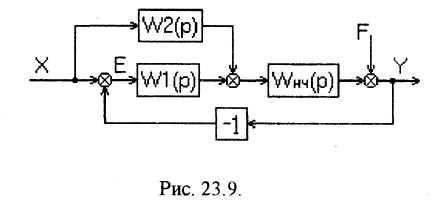
На рисунке:

Wl(p) - передаточная функция последовательного корректирую­щего устройства;

W2(p) - передаточная функция параллельного корректирующего устройства;

W_НЧ(р) - передаточная функция неизменяемой части системы.

Передаточная функция представленной комбинированной систе­мы имеет вид

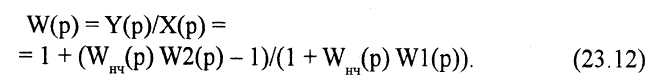
Если передаточную функцию параллельного корректирующего устройства сделать обратной передаточной функции неизменяемой части объекта

то передаточная функция комбинированной системы становится рав­ной W(p) = 1. То есть эта система превращается в идеальную следя­щую систему.

Передаточная функция комбинированной системы по сигналу ошибки

Очевидно, что при выполнении условия (23.13) ошибка управле­ния при возникновении вредных внешних воздействий или отклоне­ний параметров системы от первоначально заданных будет равна нулю. Во многих ЭМС объект управления содержит интегрирующие звенья. Тогда W2(p) в соответствии с (23.13) будет иметь дифференцирующие звенья, реализация которых весьма затруднительна. Часто прибегают к аппроксимациям, производя замену физически нереализуемой фун­кции близкой к ней физически реализуемой передаточной функцией, что дает возможность создать квазиинвариантную систему, мало отли­чающуюся от инвариантной по точности управления. Например, заме­няют оператор р на множитель (1 + рТ)/Т, причем постоянная времени Т - достаточно велика.

Использование комбинированного управления позволяет получить лучшие качественные показатели системы управления, а также сни­зить требования к основному каналу.