3.3. Формирование ску ца Мура
Следующим шагом необходимо составить систему канонических уравнений (СКУ) ЦА Мура. Делаем это по общим правилам составления СКУ по прямой таблице переходов. В результате произведения этого действия получается следующая система:
S
1(t+1)=S0
S2(t+1)=S1&X0 v S6&!X0
S3(t+1)= S1&!X0 v S2
S4(t+1)=S3
S5(t+1)=S4
S6(t+1)=S5
S7(t+1)=S6&X0
S8(t+1)=S7
S9(t+1)=S8
S10(t+1)=S9&X1
S11(t+1)=S10
S12(t+1)=S9&!X1
S13(t+1)=S11 v S12
СВФ ЦА Мура:
y
0=S0
y1=S1
y2=S2
y3=S3
y4=S4
y5=S5
y6=S6
y7=S7
y8=S8
y9=S9
y10=S10
y11=S11
y12=S12
yk=S13
Чтобы выбрать вариант кодирования, наиболее близкий к оптимальному, необходимо реализовать метод, основанный на выборе «соседнего» варианта кодирования, т.к. по заданию итоговая схема должна быть на JK-триггерах. Для этого составляется следующая диаграмма Вейча:
Исходя из этой диаграммы, мы получаем следующую таблицу кодирования:
Кодирование состояний: Неиспользуемые кодовые группы:
S(t) |
Q1 |
Q2 |
Q3 |
Q4 |
S0 |
0 |
1 |
1 |
0 |
S1 |
0 |
1 |
1 |
1 |
S2 |
0 |
1 |
0 |
1 |
S3 |
0 |
0 |
1 |
1 |
S4 |
0 |
0 |
0 |
1 |
S5 |
0 |
0 |
0 |
0 |
S6 |
0 |
1 |
0 |
0 |
S7 |
1 |
1 |
0 |
0 |
S8 |
1 |
0 |
0 |
0 |
S9 |
1 |
0 |
0 |
1 |
S10 |
1 |
0 |
1 |
1 |
S11 |
1 |
0 |
1 |
0 |
S12 |
1 |
1 |
0 |
1 |
S13 |
1 |
1 |
1 |
1 |
Q1 |
Q2 |
Q3 |
Q4 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
Q(t) |
Q(t+1) |
J |
K |
0 |
0 |
0 |
× |
0 |
1 |
1 |
× |
1 |
0 |
× |
1 |
1 |
1 |
× |
0 |
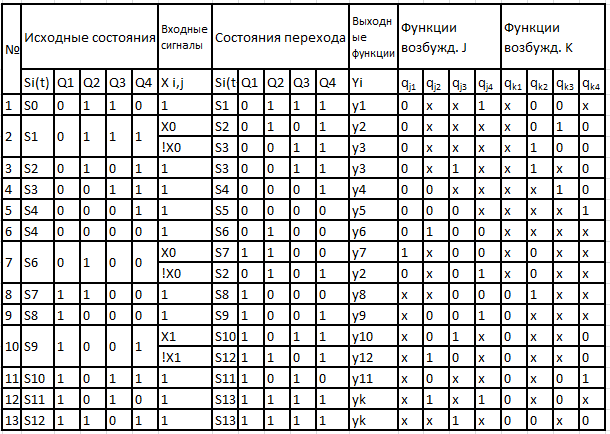
3.4. Синтез функции возбуждения и выхода
Используя таблицу кодирования состояний, прямую таблицу переходов Мура и матрицу переходов для JK триггера составим таблицу синтеза функций возбуждения и выхода.
3.4. Построение схемы на заданной элементарной базе
Принципиальная схема будет реализована на базе серии К155. В схеме будем использовать дешифратор ИД3, имеющий инверсные выходы, на которых будут формироваться инверсные состояния. Для достижения максимального быстродействия и минимальных аппаратных затрат удобнее работать с инверсными состояниями. Поэтому возьмем двойное отрицание от каждой функции возбуждения.
=
От выходных функций также берем двойное отрицание.
Рассмотрим работу схемы включение и управление схемой, то есть схему пуска, останова и инициализации.
Схема управляется тремя сигналами: START, STOP и RESERT.
Сигнал START запускает автомат, при этом запрещается дальнейшая работа.
После прихода сигнала STOP работа завершается. При выдаче сигнала yk схема автоматически останавливается, устанавливаясь в исходное состояние. Для устойчивой работы схемы необходимо сгладить помехи на шине питания. Для фильтрации частотных помех необходимо в непосредственной близости от корпуса каждой микросхемы на входах питания разместить конденсаторы по 68 нФ каждый.
С триггеров DD10.1, DD10.2 ,DD11.1 и DD11.2 сигналы Q1Q2Q3Q4 поступают на входы дешифратора DD12. На выходах дешифраторы получаем инвертированные состояния. С помощью логических элементов DD1, DD2.1, DD2.2, DD3.1 - DD3.4, DD4, DD5.1, DD5.2, DD6, DD13.1 – DD13.6, DD14.1 – DD14.6, DD15.1, DD15.2 формируем функции возбуждения для триггеров и выходные функции.
При достижении конечного состояния управляющий триггер DD8 сбрасывается в ноль.
Принципиальная схема в приложении.