21. Тригонометрические ряды Фурье
В
различных отраслях науки, в том числе,
в физике приходится иметь дело с
периодическими явлениями. Простейший
пример – электрические колебания.
Периодической называется функция
,
для которой существует такая величина,
называемая периодом, что
.
Простейшими
периодическими
функциями являются тригонометрические
функции вида
,
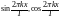где
–
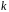целое число, называемые гармониками.
Представление периодической функции
в виде суммы гармоник называется
гармоническим анализом. В случае, когда
такая сумма бесконечна, мы получаем
тригонометрический ряд, называемый
рядом Фурье.
Итак,
пусть непрерывная
периодическая
функция
представлена в виде тригонометрического
ряда:
.
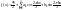Возникает вопрос: как найти коэффициенты
?
Воспользуемся тем, что гармоники обладают следующим свойством:
,
,
,
,
,
,
.
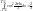Теперь
для того, чтобы, например, найти
умножим обе части равенства
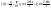на
и проинтегрируем на отрезке
.
С учетом свойств гармоник в правой
части равенства останется только
слагаемое
,
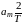а в левой части – выражение
.
Отсюда мы получим
.
Умножая
на
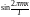и интегрируя, получим
.
А
для того, чтобы получить
,
нужно просто проинтегрировать обе
части равенства
на отрезке
.
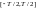Таким образом, непрерывная периодическая функция представима в виде следующего тригонометрического ряда Фурье:
,
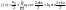где
,
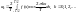В
случае, когда периодическая функция
имеет точки
разрыва,
ее также можно раскладывать в ряд Фурье,
но равенство функции и суммы ряда будет
только в точках непрерывности функции.
В точках разрыва ряд Фурье будет
сходиться к полусумме значений функции
слева и справа от точки разрыва:
.
Возможно
разложение функции в ряд Фурье с помощью
MAXIMы.
Мы получим все коэффициенты ряда Фурье
для функции
,
заданной на отрезке
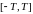и
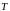-периодически
продолженной на всю вещественную ось,
если введем load(fourie);
fourier(f(x),x,t)
и нажмем Shift+Enter.
22.Пример.
Получим коэффициенты ряда Фурье для
функции
.
Для этого введем load(fourie);
fourier(%e^x,x,%pi),
нажмем Shift+Enter
и
получим
Мы
видим, что коэффициенты содержат
выражения
.
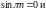
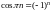Поэтому преобразуем коэффициенты:
Для
того, чтобы не только вычислить
коэффициенты ряда Фурье, но и получить
разложение функции
,
заданной на отрезке
и
-периодически
продолженной на всю вещественную ось
в ряд Фурье, следует
ввести load(fourie); totalfourier (f(x),x,T) и нажать Shift+Enter.
П р и м е р. Для разложения в ряд Фурье функции из предыдущего примера введем load(fourie); totalfourier (%e^x, x, %pi). При этом получим разложение
23.Дифференциальные уравнения
Дифференциальным
уравнением называется соотношение
вида
.
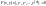Решить дифференциальное уравнение –
это значит, определить функцию
,
удовлетворяющее этому соотношению,
возможно, в неявном или параметрическом
виде.
Простейшее
дифференциальное уравнение вида
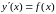мы уже решали, так как находили
.
Мы знаем, что интеграл определяется с
точностью до произвольного постоянного
слагаемого. То есть решение простейшего
дифференциального уравнения содержит
произвольную постоянную. Решения более
сложных дифференциальных уравнений
также находятся с точностью до
произвольных постоянных. Любую функцию,
удовлетворяющую дифференциальному
уравнению, мы будем называть частным
решением
этого уравнения, совокупность частных
решений назовем общим
решением
дифференциального уравнения.
Порядок
дифференциального уравнения определяется
наивысшим порядком входящих в него
производных. Поэтому дифференциальное
уравнение вида
считается дифференциальным уравнением
-го
порядка.
Так же, как не любая функция может быть проинтегрирована, и представлена в виде элементарных функций, так и не любое дифференциальное уравнение имеет решение, выражающееся через элементарные функции. Класс дифференциальных уравнений, интегрируемых в квадратурах, узок. Мы изучим несколько классов дифференциальных уравнений, интегрируемых в квадратурах, а также рассмотрим некоторые приближенные методы решения дифференциальных уравнений. Кроме того, мы рассмотрим некоторые задачи, связанные с применением дифференциальных уравнений.