
- •16. Степенные ряды
- •17.Способы определения радиуса сходимости степенного ряда
- •18.Связь между коэффициентами степенного ряда и его суммой
- •19.Примеры разложения функций в ряды Тейлора
- •20. Примеры приложений рядов Тейлора.
- •21. Тригонометрические ряды Фурье
- •23.Дифференциальные уравнения
- •24.Дифференциальное уравнение первого порядка с разделяющимися переменными
- •26.Однородное дифференциальное уравнение первого порядка
14.
Признак Лейбница сходимости
знакочередующегося ряда.
Пусть члены положительной последовательности
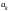 ,
монотонно убывая, стремятся к нулю при
,
монотонно убывая, стремятся к нулю при
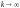 .
Тогда ряд
.
Тогда ряд
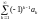 сходится.
сходится.
Доказательство.
Рассмотрим последовательность четных
частных сумм
 .
Очевидно, что с ростом
.
Очевидно, что с ростом
 значения
значения
 возрастают. Теперь запишем эту же
частную сумму в ином виде:
возрастают. Теперь запишем эту же
частную сумму в ином виде:
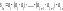 .
Очевидно, что
.
Очевидно, что
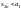 .
Таким образом, мы имеем монотонно
возрастающую ограниченную сверху
последовательность
.
По одному из свойств последовательностей
существует
.
Таким образом, мы имеем монотонно
возрастающую ограниченную сверху
последовательность
.
По одному из свойств последовательностей
существует
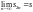 .
Итак, последовательность частных сумм
с четными номерами имеет предел. Что
же с нечетными частными суммами?
.
Итак, последовательность частных сумм
с четными номерами имеет предел. Что
же с нечетными частными суммами?
Так
как
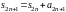 и
и
 ,
то существует
,
то существует
 .
Следовательно, существует
.
Следовательно, существует
 .
.
Пример.
Ряд
 сходится по признаку Лейбница при любом
сходится по признаку Лейбница при любом
 .
.
В
предыдущем примере, опираясь на
интегральный признак, мы показали, что
этот ряд при
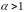 сходится абсолютно. При
сходится абсолютно. При
 ряд не может абсолютно сходиться. Но
он сходится по признаку Лейбница.
ряд не может абсолютно сходиться. Но
он сходится по признаку Лейбница.
Ряд, сходящийся, но не сходящийся абсолютно, называется условно сходящимся.
15.Пусть
 – последовательность функций, заданных
на одном и том же множестве, причем при
каждом значении
– последовательность функций, заданных
на одном и том же множестве, причем при
каждом значении
 числовой ряд
числовой ряд
 сходится. Тогда мы можем рассматривать
функциональный ряд
сходится. Тогда мы можем рассматривать
функциональный ряд
 на множестве
на множестве
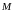 и исследовать свойства функции
и исследовать свойства функции
 –
суммы ряда – на том же множестве
.
–
суммы ряда – на том же множестве
.
В
связи с вопросами сходимости функциональных
рядов отметим следующий из теоремы
сравнения мажорантный
признак
сходимости функционального ряда: если
 такое
что
такое
что
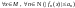 и ряд с положительными членами
и ряд с положительными членами
 сходится,
то функциональный ряд
сходится,
то функциональный ряд
 абсолютно сходится на множестве
.
абсолютно сходится на множестве
.
16. Степенные ряды
Простейшим
примером функционального ряда является
степенной ряд – ряд вида
 .
Числа
.
Числа
 ,
называются коэффициентами степенного
ряда. Поскольку простой заменой
переменной
,
называются коэффициентами степенного
ряда. Поскольку простой заменой
переменной
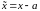 исходный степенной ряд превращается
в ряд
исходный степенной ряд превращается
в ряд
 ,
мы будем рассматривать только степенные
ряды вида
,
мы будем рассматривать только степенные
ряды вида
 .
Очевидно, что такой ряд обязательно
сходится в точке
.
Очевидно, что такой ряд обязательно
сходится в точке
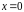 .
Ответом на вопрос об области сходимости
степенного ряда дает
.
Ответом на вопрос об области сходимости
степенного ряда дает
Теорема
Абеля.
Пусть ряд
 сходится в точке
сходится в точке
 ,
тогда он сходится, причем абсолютно,
при
,
тогда он сходится, причем абсолютно,
при
 .
.
Пусть
ряд
 расходится в точке
расходится в точке
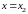 ,
тогда он расходится при
,
тогда он расходится при
 .
.
Доказательство.
Так как ряд
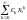 сходится, то общий член этого ряда
стремится к нулю, и значит, ограничен,
то есть,
сходится, то общий член этого ряда
стремится к нулю, и значит, ограничен,
то есть,
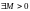 тчо
тчо
 .
.
Пусть
 тогда
тогда
 .
Так как ряд
.
Так как ряд
 сходится, то по теореме сравнения
абсолютно сходится ряд
сходится, то по теореме сравнения
абсолютно сходится ряд
 .
.
Так
как
 расходится, то
расходится, то
 не может сходиться ни при каких значениях
не может сходиться ни при каких значениях
 ,
так как в противном случае он бы сходился,
в соответствии с доказанной частью
теоремы, и при
,
так как в противном случае он бы сходился,
в соответствии с доказанной частью
теоремы, и при
 .
.
Из
теоремы Абеля следует, в частности, что
область сходимости степенного ряда
 представляет собой некоторый интервал
представляет собой некоторый интервал
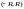 ,
а область расходимости – внешность
этого интервала. Что касается двух
точек
,
а область расходимости – внешность
этого интервала. Что касается двух
точек
 ,
являющихся границами этого интервала,
то сходимость или расходимость ряда в
этих точках следует проверять для
каждой функции индивидуально.
,
являющихся границами этого интервала,
то сходимость или расходимость ряда в
этих точках следует проверять для
каждой функции индивидуально.
Число
 называется радиусом
сходимости
степенного ряда. Интервал
называется радиусом
сходимости
степенного ряда. Интервал
 называется интервалом
сходимости
степенного ряда.
называется интервалом
сходимости
степенного ряда.
17.Способы определения радиуса сходимости степенного ряда
1.
В соответствии с признаком Даламбера
если
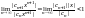 ,
то
,
то
 сходится, если
сходится, если
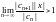 ,
то ряд
,
то ряд
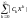 расходится. Следовательно, при
расходится. Следовательно, при
 имеем:
имеем:
 или
или
 .
.
2.
Аналогично используя признак Коши,
получим
 .
.
П
р и м е р 1. Найти область сходимости
степенного ряда
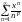 .
Найдем радиус сходимости. Здесь
.
Найдем радиус сходимости. Здесь
 .
Следовательно,
.
Следовательно,
 .
.
Проверим
сходимость в точке
 .
Имеем ряд
.
Имеем ряд
 ,
который сходится, если
,
который сходится, если
 и расходится, если
и расходится, если
 .
.
Проверим
сходимость в точке
 .
Имеем ряд
.
Имеем ряд
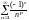 ,
который сходится, если
,
который сходится, если
 и расходится, если
и расходится, если
 .
.
Замечание.
Внутри
интервала сходимости ряд можно почленно
интегрировать и дифференцировать любое
число раз. Это значит, что если
 ,
то 1)
,
то 1)
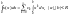 ,
,
2)
 .
.
18.Связь между коэффициентами степенного ряда и его суммой
Итак,
пусть
 .
Положим
,
тогда получим:
.
Положим
,
тогда получим:
 .
.
Возьмем
производную от членов ряда и его суммы:
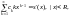 и положим
.
Тогда
и положим
.
Тогда
 .
Продолжая процесс дифференцирования,
получим:
.
Продолжая процесс дифференцирования,
получим:
 .
.
То
есть,
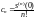 .
Таким образом, коэффициенты степенного
ряда являются коэффициентами
формулы Тейлора
для суммы ряда.
.
Таким образом, коэффициенты степенного
ряда являются коэффициентами
формулы Тейлора
для суммы ряда.
Поставим
вопросы: если для произвольной функции
 ,
имеющей бесконечное число производных
в точке
построить ряд
,
имеющей бесконечное число производных
в точке
построить ряд
 ,
называемый рядом
Тейлора
функции
,
называемый рядом
Тейлора
функции
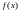 ,
то
,
то
1) где он будет сходиться, и
2)
если будет сходиться, то будет ли
сходиться к самой функции ?
?
Ответы на поставленные вопросы.
1)
Так как ряд Тейлора
 –
это степенной ряд, то для него обычным
образом можно находить радиус и интервал
сходимости. То есть,
–
это степенной ряд, то для него обычным
образом можно находить радиус и интервал
сходимости. То есть,
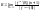 .
.
2)
Так как частная сумма ряда Тейлора –
это многочлен из формулы Тейлора
 ,
то разность между частной суммой и
функцией
согласно формуле Тейлора есть
остаточный член формулы Тейлора. Мы
его рассматривали в форме Лагранжа:
,
то разность между частной суммой и
функцией
согласно формуле Тейлора есть
остаточный член формулы Тейлора. Мы
его рассматривали в форме Лагранжа:
 .
Таким образом, если внутри интервала
сходимости остаточный член формулы
Тейлора стремится к нулю с ростом
,
то сумма ряда Тейлора совпадает с
исходной функцией, по которой построен
ряд. И тогда говорят, что функция
представима в виде ряда Тейлора, то
есть
.
Таким образом, если внутри интервала
сходимости остаточный член формулы
Тейлора стремится к нулю с ростом
,
то сумма ряда Тейлора совпадает с
исходной функцией, по которой построен
ряд. И тогда говорят, что функция
представима в виде ряда Тейлора, то
есть
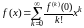 .
.
