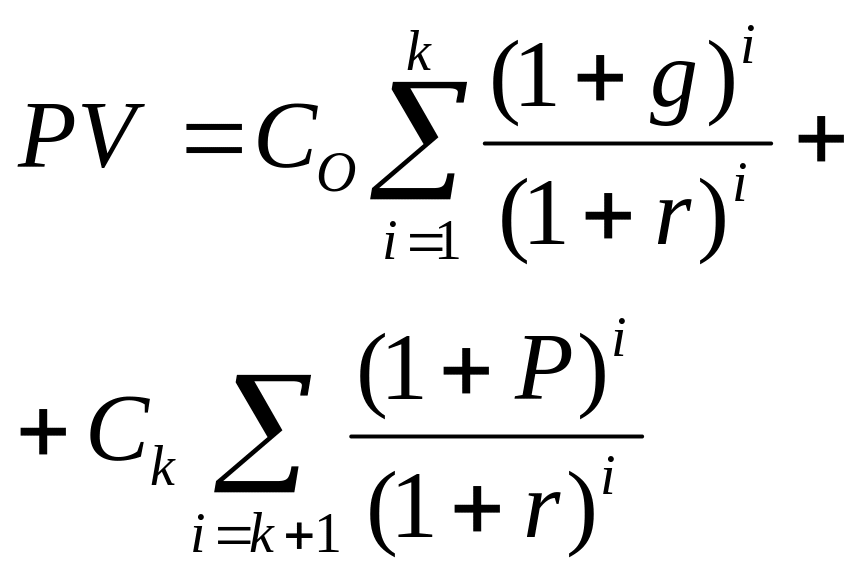44. Майбутня вартість грошей та її зміст. Розрахунок майбутньої вартості грошей з урахуванням ануїтетів. Використання процентного фактора у розрахунках майбутньої вартості грошей.
Майбутня вартість (FV) являє собою суму інвестованих у теперішній момент коштів, в яку вони мають перетворитися через певний проміжок часу з урахуванням певної ставки процента.
МВГ – сума інвестованих в даний момент грошових засобів, у яку вони перетворяться ч/з певний пер-д часу з урах-ням певної ставки %. Гроші, які люди мають на даний момент, дорожчі, ніж гроші, які вони матимуть у майб-му. Процес переходу від теперішньої вар-ті грошей (PV) до майбутньої вар-ті (FV) наз компаундуванням. Просте ком-ня – визнач майб вар-ті грошей, вкладених одночасно на певний термін під певний % (FV = PV*(1+i)^n, де i - % ставка, виражена десятковим дробом; n – кількість інтервалів, по яких відб-ся розрах-к %-х платежів у загальному обумовленому пер-ді часу.).
Ануїтет – рівномірні платежі чи надход-ня грошей ч/з однакові інтервали часу при викор-ні однакової % ставки. Представлення послідовності грош потоків у виді ануїтету суттєво спрощує процес нарощування (дисконтування) вар-ті, дає можл-ть викор-ти набір спрощених формул зі стандартними зн-нями окремих спеціальних пок-ків. Ком-ня ануїтетів – визнач-я майбут вар-ті грошей, вкладених рівними частками ч/з рівні проміжки часу під певний %(звичайна рента, вексельна рента)( FVЗ.А.=R*(( (1+i)^n-1)/i) ). Звичайна рента – рента, вклади по якій проводяться у кінці кожного пер-ду. Вексельна рента (ануїтет не зобов’язання)– та, вклади по якій проводяться на початку кожного пер-ду. FVАН. З.=R*[( (1+i)^(n+1)-1)/i)-1].
45. Теперішня вартість грошей та її зміст
Теперішня вартість— Ця вартість служить основою для порівняння прибутковості різних проектів та інвестицій за певний період. Отже, теперішня вартість — це грошова вартість майбутніх надходжень чи доходів з поправкою на ставки дисконту (капіталізації).
Дисконтна ставка — це процентна ставка, яка застосовується до майбутніх платежів, щоб врахувати ризик і непевність, пов'язану з фактором часу.Для підрахунку теперішньої вартості слід визначити ставку дисконту, що враховувала б ризикованість певного проекту чи інвестицій. Існує просте правило:Високий ризик означає високу ставку дисконту (капіталізації), малий ризик означає низьку дисконтну ставку.
Дисконтування – процес, протилежний компаундируванню. Це визначення поточної вартості грошей (PV).Коли рівень ризику визначено, далі слід скоригувати майбутні доходи з урахуванням непевності часу. Загалом для оцінки дисконтних ставок використовують такі принципи: З двох майбутніх надходжень вищу дисконтну ставку матиме те, що надійде пізніше.Чим нижчий визначений рівень ризику, тим нижчою повинна бути ставка дисконту
тоді
, (1.6)
де PV – теперішня вартість коштів;
FV — майбутня вартість коштів;
R — річна ставка процента;
N — кількість років.
Якщо нарахування відсотків планується більше одного разу за рік, то розрахунок проводять за формулою:
,
(1.7)
де т — кількість нарахувань за рік, од.
Математичне рівняння для визначення теперішньої вартості ануїтету таке:
,
(1.10)
де: РVa — теперішня вартість ануїтету;
А — сума ануїтету,
R — ставка дисконту;
N — кількість років або періодів;
PVIFA - процентний фактор теперішньої вартості ануїтету
то дисконтування майбутніх грошових потоків із використанням простого процента відповідає такій формулі:
FV
РV = --------------, (4.12)
(1 + n . i)
де: РV – приведена теперішня вартість майбутнього грошового потоку;
FV – абсолютна величина майбутнього грошового потоку;
n – кількість інтервалів у плановому періоді;
i – ставка дисконтування (виражена десятковим дробом).
Оскільки майбутня вартість наявних грошових коштів у разі використання складного процента визначається за формулою (4.3):
FV = РV . (1 + i)n,
то приведена теперішня вартість майбутніх грошових потоків при використанні складного процента визначається за такою формулою:
FV 1
РV = ----------- = FV . (-------)n. (4.13)
(1 + i)n 1 + i
Можна визначити теперішню вартість майбутнього грошового потоку із використанням фінансової таблиці А-3, яка містить абсолютне значення ставки дисконтування, виходячи із рівня процентної ставки та кількості інтервалів у плановому періоді.
Частина рівняння (4.13), взята в дужки, називається фактором процента поточної вартості FVIF.
Таким чином, якщо
1 n
FVIFАi,n = (-----),
1 + i
то формула (4.13) матиме вигляд:
FV = FV . (FVIFi,n). (4.14)
де: FVIFi,n – абсолютне значення ставки дисконтування;
i – процентна ставка;
n – кількість інтервалів у плановому періоді;
46. Врахування фактора часу у розрахунках вартості облігацій і акцій.Більшість господарських операцій (придбання основних засобів, купівля/продаж цінних паперів, лізинг, одержання/погашення банківських кредитів, аналіз інвестиційних проектів тощо) породжують грошові потоки. Здійснення цих операцій супроводжується безліччю виплат і надходжень коштів, утворюючи грошовий потік, розподілений у часі. У зв’язку з цим у процесі управління фінансами підприємства виникає необхідність у проведенні спеціальних розрахунків, пов’язаних з рухом грошових потоків у різні періоди його діяльності. Ключову роль у цих розрахунках відіграє оцінка вартості грошей у часі.
Математичне дисконтування – спосіб, заснований на вирішенні задачі зворотного визначення майбутньої вартості. При проведенні розрахунків тут використовується процентна ставка. З урахуванням прийнятих раніше позначень формула дисконтування за ставкою r буде мати вигляд:
PV = FV/(1 + r*n) = FV/(1 + r*t/B), (4)
Дохід банку (FV – PV) називають дисконтом, а використовувану норму приведення r – декурсивною ставкою процентів.
Методи оцінки акцій та облігацій
Вид акції |
Розрахункова формула |
Умовні позначення |
Акції, дивіденди по яких зростають з постійним темпом приросту |
|
PV – вартість акцій C – базовий розмір дивіденду r – прийнятий рівень процентного доходу g – темпи приросту |
Акції, дивіденди по яких зростають із змінним темпом приросту |
|
С0 – дивіденд, що виплачується у базовий період часу Ck – дивіденд, що прогнозується у k-му періоді g – темпи приросту у k-му періоді Р – темпи приросту у наступних періодах |
Безкупонні облігації |
|
PV – теперішня ринкова вартість облігації FV – номінальна вартість облігації k – період погашення r – ринковий процентний дохід |
Облігації з постійним купонним доходом |
|
С – однакові постійні купонні надходження за періодами |
Безстрокові облігації |
|
|
