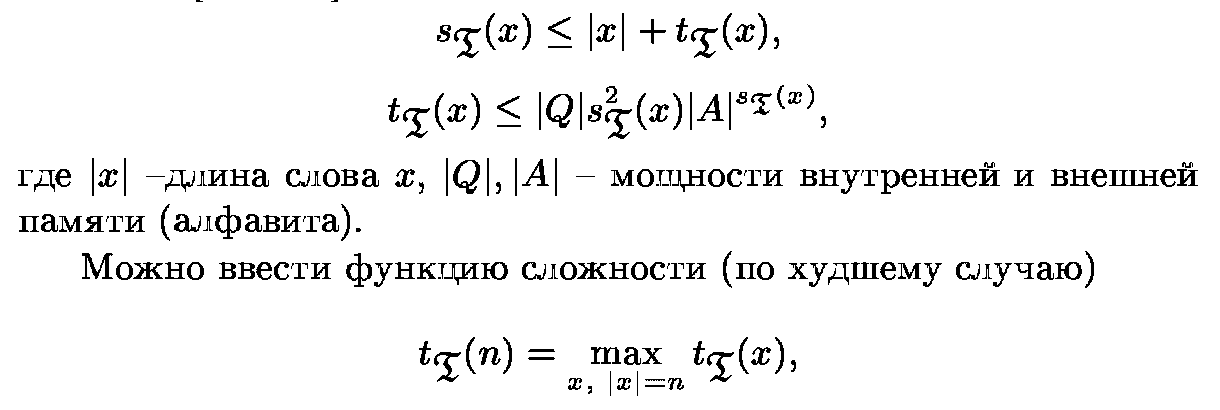- •Понятие алгоритма, его свойства.
- •Возникновение и история развития теории алгоритмов.
- •Основные определения.
- •Сравнительные оценки алгоритмов.
- •Система обозначений в анализе алгоритмов.
- •Классификация алгоритмов по виду функции трудоёмкости.
- •Асимптотический анализ функций.
- •Элементарные операции в языке записи алгоритмов.
- •Трудоемкость алгоритмов и временные оценки.
- •10. Понятия рекурсии и вычислимой функции.
- •Простейшие рекурсивные функции.
- •12. Операция суперпозиции частичных функций.
- •13. Операция примитивной рекурсии частичных функций.
- •14. Операция минимизации арифметических функций.
- •15. Частично рекурсивные функции и тезис Чёрча.
- •16. Понятие алгоритма как абстрактной машины.
- •17. Алгоритмическая машина Поста (определение, команды, принцип работы).
- •18. Алгоритмическая машина Тьюринга (определение, команды, схема функционирования).
- •19. Алгоритмически неразрешимые задачи (примеры).
- •20. Теоретический предел трудоемкости задачи.
- •21. Сложностные классы задач.
- •Класс npc (np – полные задачи)
- •Класс npc (np – полные задачи)
- •Примеры np – полных задач
- •23. Полиномиально проверяемые задачи.
- •24. Анализ алгоритма точного решения задачи о сумме
- •Формулировка задачи и асимптотическая оценка
- •V содержит 1 слагаемое вариантов;
- •V содержит 2 слагаемых вариантов;
- •V содержит 3 слагаемых вариантов;
- •Алгоритм точного решения задачи о сумме (метод перебора)
- •Анализ алгоритма точного решения задачи о сумме
V содержит 1 слагаемое вариантов;
V содержит 2 слагаемых вариантов;
V содержит 3 слагаемых вариантов;
и т.д. до проверки одного варианта с N слагаемыми.
Поскольку
сумма биномиальных коэффициентов для
степени N равна - ![]() и
для каждого варианта необходимо выполнить
суммирование (с оценкой O(N)) для проверки
на V, то оценка сложности алгоритма в
худшем случае имеет вид:
и
для каждого варианта необходимо выполнить
суммирование (с оценкой O(N)) для проверки
на V, то оценка сложности алгоритма в
худшем случае имеет вид:
![]() (7.1)
(7.1)
Алгоритм точного решения задачи о сумме (метод перебора)
Определим вспомогательный массив, хранящий текущее сочетание исходных чисел в массиве S, подлежащих проверке на V – массив Cnt[j], элемент массива равен «0», если число S[j] не входит в V и равен «1», если число S[j] входит в V
Решение получено, если V = S[j]*Cnt[j].
Могут быть предложены следующие две реализации механизма полного перебора вариантов:
перебор по всевозможным сочетаниям из k элементов по N, т.е. сначала алгоритм пытается представить V как один из элементов массива S, затем перебираются все возможные пары, затем все возможные тройки и т.д.;
перебор по двоичному счётчику, реализованному в массиве Cnt: Вторая идея алгоритмически более проста и сводится к решению задаче об увеличении двоичного счётчика в массиве Cnt на «1»:
при 00...0111 увеличение на «1» приводит к сбросу всех правых «1» и установке в «1» следующего самого правого «0»;
при 00...1000, когда последний элемент счетчика равен «0» увеличение на «1» приводит к переустановке последнего элемента в массиве Cnt с «0» в «1».
Рассматривая массив Cnt как указатель на элементы массива S, подлежащие суммированию в данный момент, мы производим суммирование и проверку на V, до тех пор, пока решение не будет найдено или же безрезультатно будут просмотрены все возможные варианты.
Таким образом, алгоритм точного решения задаче о сумме методом прямого перебора имеет в формальной системе языка высокого уровня следующий вид:
TASKSUM(S,N,V; CNT,FL) FL <-- false i <-- 1 repeat Cnt[i] <-- 0 i <-- i+1 Until i > N Cnt[N] <-- 1 Repeat Sum <-- 0 i <-- 1 Repeat Sum <-- Sum + S[i] * Cnt[i] |
i <-- i+1 Until i > N if Sum = V FL <-- true Return (Cnt,FL) j <-- N While Cnt[j] = 1 Cnt[j] = 0 j <-- j-1 Cnt[j] <-- 1 Until Cnt[0] = 1 Return(Cnt,FL) |
Анализ алгоритма точного решения задачи о сумме
Рассмотрим лучший и худший случай для данного алгоритма:
) В лучшем случае, когда последний элемент массива совпадает со значением V: V=S[N],необходимо выполнить только одно суммирование, что приводит к оценке:
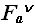 (N)=Q(N);
(N)=Q(N);В худшем случае, если решения вообще нет, то придется проверить все варианты, и (N) = Q (N*
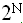 ).
).
Получим детальную оценку для худшего случая, используя принятую методику подсчета элементарных операций:
(N)
= 2+N*(3+2)+2+(
-1)*{2+N*(3+5)+1+1+![]() +2+2}
(7.2)
+2+2}
(7.2)
Для получения значения - количества операций, необходимых для увеличения счетчика на «1» рассмотрим по шагам проходы цикла While, в котором выполняется эта операция:
-
CNT
Количество проходов в While
Операций
001
1
6+2
010
0
2
011
2
2*6+2
100
0
2
101
1
6+2
110
0
2
111
3
3*6+2
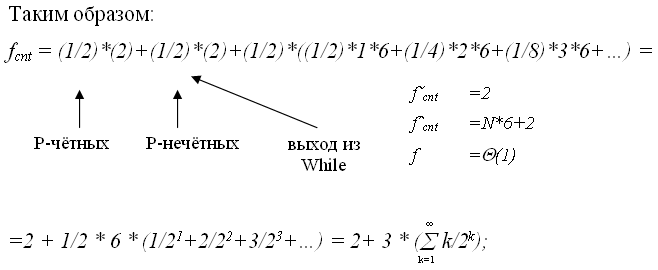
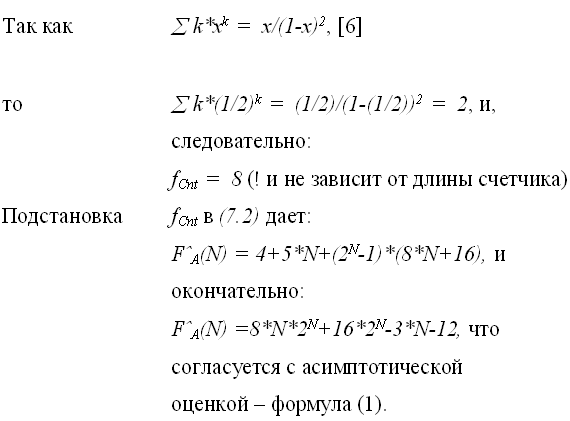
4*
Очевидно,
что для решения некоторой массовой
проблемы можно придумать не один
алгоритм. Поэтому важно иметь критерии,
позволяющие оценивать разработанные
алгоритмы.
 Время
обычно интересует в наибольшей степени,
поэтому именно на оценке временной
сложности алгоритмов мы остановимся
подробнее.
Временная
сложность.
Время
обычно интересует в наибольшей степени,
поэтому именно на оценке временной
сложности алгоритмов мы остановимся
подробнее.
Временная
сложность.
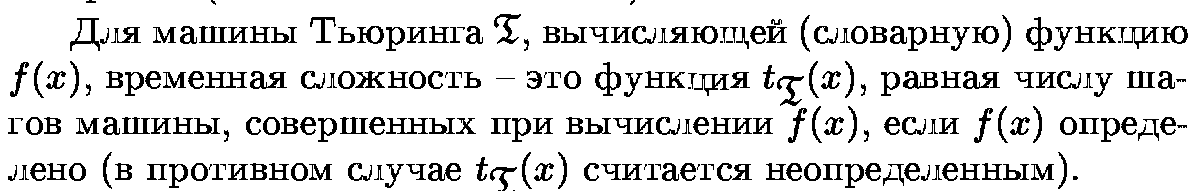 Время
решения индивидуальной задачи зависит
от скорости вычислителя, языка
программирования и многого другого.
Определяя качество алгоритма имеет
смысл не учитывать эти факторы. Вместо
времени мы будем оценивать количество
характерных операций, которое необходимо
выполнить, решая индивидуальную задачу
данным алгоритмом.
Рассмотрим
конкретную проблему (индивидуальную
задачу), заданную N словами памяти.
Под
трудоемкостью алгоритма для данного
конкретного входа – Fa(N), будем понимать
количество «элементарных» операций
совершаемых алгоритмом для решения
конкретной проблемы в данной формальной
системе.
При
более детальном анализе трудоемкости
алгоритма оказывается, что не всегда
количество элементарных операций,
выполняемых алгоритмом на одном входе
длины N, совпадает с количеством операций
на другом входе такой же длины. Это
приводит к необходимости введения
специальных обозначений, отражающих
поведение функции трудоемкости данного
алгоритма на входных данных фиксированной
длины.
Пусть
DА – множество индивидуальных задач
(конкретных проблем) данной массовой
проблемы.
DА
– задание индивидуальной задач и |D| =
N.Пусть
D
Пусть
DNDА
– множество всех индивидуальных задач,
имеющих мощность N, т.е. DN
D=
{DN :
|D| = N}.
Тогда
данный алгоритм, решая различные задачи
размерности N, будет выполнять в каком-то
случае наибольшее количество операций,
а в каком-то случае наименьшее количество
операций.
^ Можно
ввести следующие обозначения (функции
оценки трудоемкости):
1. (N)
– худший случай – наибольшее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:Fa
(N)
= max {Fa (D)} – худший случай на
DFaN
DDN
Временной
сложностью в наихудшем случае (верхней
оценкой сложности алгоритма) называют
функцию T(N), равную максимальному времени
выполнения алгоритма для всех
индивидуальных задач размером N.
Часто
бывает полезно определить не верхнюю
оценку сложности, а среднюю, хотя это,
как правило, сложнее.
Точную
верхнюю оценку сложности получить тоже
не всегда просто. В таком случае
ограничимся определением порядка роста
верхней оценки временной сложности.
Функция
f(n) имеет порядок роста функции g(n), если
найдется такая константа C, что для любых
n выполняется неравенство: f(n) <
C*g(n)
2. (N)
– лучший случай – наименьшее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:Fa
(N)
= min {Fa (D)} – лучший случай на DFaN
DDN
3Fa(N)
– средний случай – среднее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:.
Fa(N)
= (1 / |DN
{Fa (D)} – средний случай на D|)*N
DDN
Емкостная
сложность.
Время
решения индивидуальной задачи зависит
от скорости вычислителя, языка
программирования и многого другого.
Определяя качество алгоритма имеет
смысл не учитывать эти факторы. Вместо
времени мы будем оценивать количество
характерных операций, которое необходимо
выполнить, решая индивидуальную задачу
данным алгоритмом.
Рассмотрим
конкретную проблему (индивидуальную
задачу), заданную N словами памяти.
Под
трудоемкостью алгоритма для данного
конкретного входа – Fa(N), будем понимать
количество «элементарных» операций
совершаемых алгоритмом для решения
конкретной проблемы в данной формальной
системе.
При
более детальном анализе трудоемкости
алгоритма оказывается, что не всегда
количество элементарных операций,
выполняемых алгоритмом на одном входе
длины N, совпадает с количеством операций
на другом входе такой же длины. Это
приводит к необходимости введения
специальных обозначений, отражающих
поведение функции трудоемкости данного
алгоритма на входных данных фиксированной
длины.
Пусть
DА – множество индивидуальных задач
(конкретных проблем) данной массовой
проблемы.
DА
– задание индивидуальной задач и |D| =
N.Пусть
D
Пусть
DNDА
– множество всех индивидуальных задач,
имеющих мощность N, т.е. DN
D=
{DN :
|D| = N}.
Тогда
данный алгоритм, решая различные задачи
размерности N, будет выполнять в каком-то
случае наибольшее количество операций,
а в каком-то случае наименьшее количество
операций.
^ Можно
ввести следующие обозначения (функции
оценки трудоемкости):
1. (N)
– худший случай – наибольшее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:Fa
(N)
= max {Fa (D)} – худший случай на
DFaN
DDN
Временной
сложностью в наихудшем случае (верхней
оценкой сложности алгоритма) называют
функцию T(N), равную максимальному времени
выполнения алгоритма для всех
индивидуальных задач размером N.
Часто
бывает полезно определить не верхнюю
оценку сложности, а среднюю, хотя это,
как правило, сложнее.
Точную
верхнюю оценку сложности получить тоже
не всегда просто. В таком случае
ограничимся определением порядка роста
верхней оценки временной сложности.
Функция
f(n) имеет порядок роста функции g(n), если
найдется такая константа C, что для любых
n выполняется неравенство: f(n) <
C*g(n)
2. (N)
– лучший случай – наименьшее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:Fa
(N)
= min {Fa (D)} – лучший случай на DFaN
DDN
3Fa(N)
– средний случай – среднее количество
операций, совершаемых алгоритмом А для
решения индивидуальных задач размерностью
N:.
Fa(N)
= (1 / |DN
{Fa (D)} – средний случай на D|)*N
DDN
Емкостная
сложность.
 Тогда:
Тогда: