Примеры np – полных задач
1 Задача о выполнимости схемы
Рассмотрим схему из функциональных элементов «и», «или», «не» с n битовыми входами и одним выходом, состоящую не более, чем из O( ) элементов – рис 6.4
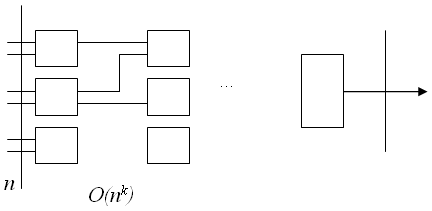
Будем понимать под выполняющим набором значений из множества {0,1} на входе схемы, такой набор входов – значения x1,…,xn, при котором на выходе схемы будет значение «1».
Формулировка задачи – существует ли для данной схемы выполняющий набор значений входа. Очевидно, что задача принадлежит классу NP – проверка предъявленного выполняющего набора не сложнее количества функциональных элементов, и следовательно не больше чем O( ).
Это была одна из первых задач, для которой была доказана ее NP полнота, т.е. любая задача из класса NP полиномиально сводима к задаче о выполнимости схемы.
Решение
этой задачи может быть получено перебором
всех
возможных
значений входа с последующей проверкой
на соответствие условию выполняющего
набора. В худшем случае придется проверить
все возможные значения входа, что
приводит к оценке 
Для
этой, как и для всех других NP–полных
задач не известен полиномиальный
алгоритм решения.
2 Задача о сумме
Уже рассмотренная задача о сумме также является NP–полной, отметим, что если количество слагаемых фиксировано, то сложность задачи является полиномиальной, так как:
для 2-х слагаемых
для 3-х слагаемых
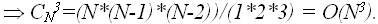
Однако
в общем случае придется перебирать 
различных
вариантов, так как по биномиальной
теореме 
,
а при a=b=1, имеем: 
3 Задача о клике
Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G.
Задача состоит в определении клики в заданном графе G
Поскольку
в полном графе на m вершинах имеется
m(m-1)/2 ребер, то проверка, является ли
данный граф полным, имеет сложность O
(
).
Очевидно, что если мы рассматриваем
подграф с m вершинами в графе G с вершинами
(m < n), то всего существует 
различных
подграфов. Если в задаче о клике количество
вершин клики фиксировано, то перебирающий
алгоритм имеет полиномиальную сложность:
Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае:
23. Полиномиально проверяемые задачи.
24. Анализ алгоритма точного решения задачи о сумме
Формулировка задачи и асимптотическая оценка
Словесно задача о сумме формулируется как задача нахождения таких чисел из данной совокупности, которые в сумме дают заданное число, классически задача формулируется в терминах целых чисел [6].
В терминах структур данных языка высокого уровня задача формулируется, как задача определения таких элементов исходного массива S из N чисел, которые в сумме дают число V (отметим, что задача относится к классу NPC).
Детальная формулировка: Дано: Массив S[i], i={1, N} и число V. Требуется: определить такие Sj, что Sj=V
Тривиальное решение определяется равенством V=Sum, где Sum= Si , условия существования решения имеют вид:
Min {S[i], i=1,N} =< V =< Sum.
Получим асимптотическую оценку сложности решения данной задачи для алгоритма, использующего прямой перебор всех возможных вариантов. Поскольку исходный массив содержит N чисел, то проверке на равенство V подлежат следующие варианты решений: