Класс npc (np – полные задачи)

Понятие NP – полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (журнал «Проблемы передачи информации», 1973,т.9, вып. 3) и основывается на понятии сводимости одной задачи к другой.

Сводимость может быть представлена следующим образом: если мы имеем задачу 1 и решающий эту задачу алгоритм, выдающий правильный ответ для всех конкретных проблем, составляющих задачу, а для задачи 2 алгоритм решения неизвестен, то если мы можем переформулировать (свести) задачу 2 в терминах задачи 1, то мы решаем задачу 2.

Таким образом, если задача 1 задана множеством конкретных проблем   , а задача 2 – множеством, и существует функция   (алгоритм), сводящая конкретную постановку задачи 2 (  ) к конкретной постановке задачи 1( ):  , то задача 2 сводима к задаче 1.

Если при этом  ( ) = O( ), т.е. алгоритм сведения принадлежит классу P, то говорят, что задача 1 полиномиально сводится к задаче 2.

Принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 – языком L2, то полиномиальная сводимость обозначается следующим образом: L2 =< pL1.

Определение класса NPC (NP-complete) или класса NP-полных задач требует выполнения следующих двух условий: во-первых, задача должна принадлежать классу NP (L є NP), и, во-вторых, к ней полиномиально должны сводиться все задачи из класса NP (Lx=< pL, для каждого Lx є NP), что схематично представлено на рис 6.2.

22. Проблема P=NP. NP-полные задачи.

2. Проблема P = NP

После введения в теорию алгоритмов понятий сложностных классов Эдмондсом (Edmonds, 1965) была поставлена основная проблема теории сложности – P = NP ? Словесная формулировка проблемы имеет вид: можно ли все задачи, решение которых проверяется с полиномиальной сложностью, решить за полиномиальное время ?

Очевидно, что любая задача, принадлежащая классу P, принадлежит и классу NP, т.к. она может быть полиномиально проверена – задача проверки решения может состоять просто в повторном решении задачи.

На сегодня отсутствуют теоретические доказательства как совпадения этих классов (P=NP), так и их несовпадения. Предположение состоит в том, что класс P является собственным подмножеством класса NP, т.е. NP \ P не пусто – рис 6.1

3. Класс npc (np – полные задачи)

Понятие NP – полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (журнал «Проблемы передачи информации», 1973,т.9, вып. 3) и основывается на понятии сводимости одной задачи к другой.

Сводимость может быть представлена следующим образом: если мы имеем задачу 1 и решающий эту задачу алгоритм, выдающий правильный ответ для всех конкретных проблем, составляющих задачу, а для задачи 2 алгоритм решения неизвестен, то если мы можем переформулировать (свести) задачу 2 в терминах задачи 1, то мы решаем задачу 2.

Таким образом, если задача 1 задана множеством конкретных проблем   , а задача 2 – множеством, и существует функция   (алгоритм), сводящая конкретную постановку задачи 2 (  ) к конкретной постановке задачи 1( ):  , то задача 2 сводима к задаче 1.

Если при этом  ( ) = O( ), т.е. алгоритм сведения принадлежит классу P, то говорят, что задача 1 полиномиально сводится к задаче 2.

Принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 – языком L2, то полиномиальная сводимость обозначается следующим образом: L2 =< pL1.

Определение класса NPC (NP-complete) или класса NP-полных задач требует выполнения следующих двух условий: во-первых, задача должна принадлежать классу NP (L є NP), и, во-вторых, к ней полиномиально должны сводиться все задачи из класса NP (Lx=< pL, для каждого Lx є NP), что схематично представлено на рис 6.2.

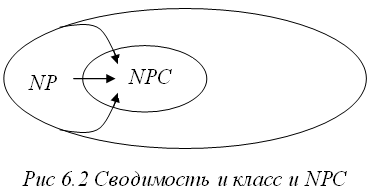
Для класса NPC доказана следующая теорема: Если существует задача, принадлежащая классу NPC, для которой существует полиномиальный алгоритм решения (F = O( )), то класс P совпадает с классом NP, т.е. P=NP.

Схема доказательства состоит в сведении любой задачи из NP к данной задаче из класса NPC с полиномиальной трудоемкостью и решении этой задачи за полиномиальное время (по условию теоремы).

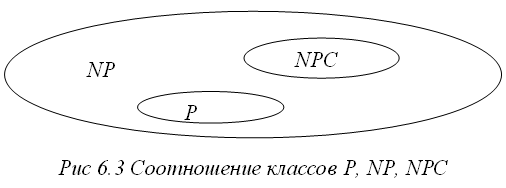
В настоящее время доказано существование сотен NP–полных задач, но ни для одной из них пока не удалось найти полиномиального алгоритма решения. В настоящее время исследователи предполагают следующее соотношение классов, показанное на рис 6.3 – P   NP, то есть NP \ P   0, и задачи из класса NPC не могут быть решены (сегодня) с полиномиальной трудоемкостью.