МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский Государственный Технический Университет имени М.Т.Калашникова»
(ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова»)
Кафедра «Мехатронные системы»
Отчет по лабораторной работе № 1
Тема: «Дискретное преобразование Фурье»
Выполнил:
студент гр. М01-311-1
Клековкин А.В.
Проверил:
Трефилов С.А.
Ижевск 2012
Содержание
Техническое задание 2
Введение 3
1. Разработка алгоритма 5
2. Разработка программы 6
3. Вычислительный эксперимент 10
Заключение 11
Литература 12
Техническое задание
Составить алгоритм и программу дискретного преобразования Фурье для функции вида:
(1)
где N=32;
Введение
Дискретное преобразование Фурье — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы преобразований:
Прямое преобразование:
(2)
Обозначения:
N — количество значений сигнала, измеренных за период, а также количество компонент разложения;
— измеренные
значения сигнала (в дискретных временных
точках с номерами
,
которые являются входными данными для
прямого преобразования и выходными для
обратного;
— N
комплексных амплитуд синусоидальных
сигналов, слагающих исходный сигнал;
являются выходными данными для прямого
преобразования и входными для обратного;
поскольку амплитуды комплексные, то по
ним можно вычислить одновременно и
амплитуду, и фазу;
—
обычная
(вещественная) амплитуда k-го синусоидального
сигнала;
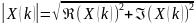(3)
— фаза
k-го синусоидального сигнала (аргумент
комплексного числа);
k
— индекс частоты. Частота k-го сигнала
равна
,
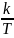где T
— период времени, в течение которого
брались входные данные.
1. Разработка алгоритма
Схема алгоритма программы дискретного преобразования Фурье представлена на рисунке 1.
Начало
Формируем массив дискретных значений функции (1)
Считаем значения Xk по формуле (2) для действительной и мнимой части.
Считаем
амплитуду сигнала
по формуле (3)
Считаем
фазу сигнала
по формуле (4)
Вывод на экран результатов
Построение графиков по полученным данным
Конец
Рисунок 1 – Схема алгоритма программы дискретного преобразования Фурье.
2. Разработка программы
Текст программы дискретного преобразования Фурье представлен на рисунке 2.
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.Threading;
namespace бпф
{
public partial class Form1 : Form
{
public Graphics g;
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
double[] x=new double[32];
double[] mas=new double[32];
double[] x_re = new double[32];
double[] x_im = new double[32];
double[] amp = new double[32];
double[] faza = new double[32];
int f = 20;
double m = Convert.ToDouble(textBox2.Text), fi = 2*Math.PI*m/32, a = Convert.ToDouble(textBox1.Text), summa_re = 0, summa_im=0;
for (int n = 0; n < 32; n++)
{
x[n] = a * Math.Sin(2 * Math.PI / 32 * n + fi);
mas[n]=n;
}
for (int k = 0; k < 32; k++)
{
for (int n = 0; n < 32; n++)
{
summa_re += x[n] * Math.Cos(2 * Math.PI * k*n / 32);
summa_im += x[n] * Math.Sin(2 * Math.PI * k*n / 32)*(-1);
}
x_re[k] = summa_re;
x_im[k] = summa_im;
summa_im = summa_re = 0;
}
Рисунок 2 – Текст программы дискретного преобразования Фурье.
for (int k = 0; k < 32; k++)
{
amp[k] = Math.Sqrt(x_re[k] * x_re[k] + x_im[k] * x_im[k]);
faza[k] = Math.Atan(x_im[k] / x_re[k]);
}
listBox1.Items.Clear();
listBox2.Items.Clear();
listBox3.Items.Clear();
listBox4.Items.Clear();
listBox5.Items.Clear();
for (int k = 0; k < 32; k++)
{
listBox1.Items.Add(x[k]);
listBox2.Items.Add(x_re[k]);
listBox3.Items.Add(x_im[k]);
listBox4.Items.Add(amp[k]);
listBox5.Items.Add(faza[k]);
}
Thread.Sleep(10);
g = panel1.CreateGraphics(); //рисуем график на панели 1
g.Clear(Color.White);
Grafik gr1 = new Grafik(mas, x, g, panel1.ClientSize, Color.Red, f, f);
Grafik gr2 = new Grafik(mas, amp, g, panel1.ClientSize, Color.Magenta, f, f/10);
Grafik gr3 = new Grafik(mas, faza, g, panel1.ClientSize, Color.Blue, f, f);
gr1.Setka(1,1);
gr1.ris();
gr2.ris();
gr3.ris();
}
private void button2_Click(object sender, EventArgs e)
{
Application.Exit();
}
}
public class Grafik
{
public double[] x, y;
public double mas_x, mas_y; //Масштаб
public Graphics graph;
public Pen myPen;
public Pen myPen2 = new Pen(System.Drawing.Color.LightBlue);
public Pen myPen3 = new Pen(System.Drawing.Color.Chocolate);
public Size size;
public int x_null = 20, y_null = 200;
public Grafik(double[] x, double[] y, Graphics graph, Size size, Color col, double mas_x, double mas_y)
{
this.x = new double[x.Length];
this.y = new double[y.Length];
this.x = x;
this.y = y;
this.graph = graph;
this.myPen = new Pen(col);
Рисунок 2 – Продолжение.
this.size = size;
this.mas_x = mas_x;
this.mas_y = mas_y;
}
private float m_x(double a)
{
float b;
b = Convert.ToInt32(a * mas_x + x_null);
return b;
}
private float m_y(double a)
{
float b;
b = Convert.ToInt32(a * (-1) * mas_y + y_null);
return b;
}
public void ris()
{
for (int i = 0; i < x.Length - 1; i++)
{
graph.DrawLine(myPen, m_x(x[i]), m_y(y[i]), m_x(x[i + 1]), m_y(y[i + 1]));
}
}
private void delenie(Pen myPen, double x1, double x2, double y1, double y2)
{
x1 = x1 * mas_x + size.Width / 2;
x2 = x2 * mas_x + size.Width / 2;
y1 = y1 * mas_y + size.Height / 2;
y2 = y2 * mas_y + size.Height / 2;
graph.DrawLine(myPen, Convert.ToInt32(x1), Convert.ToInt32(y1), Convert.ToInt32(x2), Convert.ToInt32(y2));
}
public void Setka(double shag_x, double shag_y)
{
for (double xx = x_null; xx < size.Width; xx += mas_x * shag_x)
{
graph.DrawLine(new Pen(Color.LightBlue), Convert.ToInt32(xx), 0, Convert.ToInt32(xx), size.Height);
}
for (double xx = x_null; xx > 0; xx -= mas_x * shag_x)
{
graph.DrawLine(new Pen(Color.LightBlue), Convert.ToInt32(xx), 0, Convert.ToInt32(xx), size.Height);
}
for (double yy = y_null; yy < size.Height; yy += mas_y * shag_y)
{
graph.DrawLine(new Pen(Color.LightBlue), 0, Convert.ToInt32(yy), size.Width, Convert.ToInt32(yy));
}
Рисунок 2 – Продолжение.
for (double yy = y_null; yy > 0; yy -= mas_y * shag_y)
{
graph.DrawLine(new Pen(Color.LightBlue), 0, Convert.ToInt32(yy), size.Width, Convert.ToInt32(yy));
}
Osi();
}
public void Osi()
{
graph.DrawLine(new Pen(Color.Black, 1), 0, y_null, size.Width, y_null);
graph.DrawLine(new Pen(Color.Black, 1), x_null, 0, x_null, size.Height);
}
}
}
Рисунок 2 – Продолжение.